一、单项选择题 在做进栈运算时,应先判别栈是否 (①) ,在做退栈运算时应先判别栈是否 (②) 。当栈中元素为n个,做进栈运算时发生上溢,则说明该栈的最大容量为 (③) 。为了增加内存空间的利用率和减少溢出的可能性,由两个栈共享一片连续的内存空间时,应将两栈的 (④) 分别设在这片内存空间的两端,这样,当 (⑤) 时,才产生上溢。 设n个元素的进栈序列为1,2,3,…,n,其出栈序列是p1,p2,p3,…,pn,若p1=3,则p2的值为______;设n个元素的进栈序列为p1,p2,p3,…,pn,其出栈序列是1,2,3,…,n,若p3=1,则p1的值为______。 设有一个10×10的堆成矩阵A[10][10],采取按行压缩存储的方式存放于一个一维数组B[ ]中,则数组B[ ]的容量应为______。若设A[0][0]存放于B[0],且数组A[ ][ ]的每一个数组元素在数组B[ ]中占一个数组元素位置,若按照下三角方式压缩仔放,A[8][5]在数组B[ ]中的位置是______;按照上i角方式压缩存放,A[8][5]在数组B( )中的位置是______。 二、综合应用题1. 常用的阶乘函数定义如下:
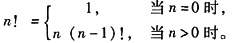
对应的求阶乘的递归算法为:
Long Factorial (long n){
if (n==0) return(1); //终止递归的条件
else return (n%Factorial (n-1)); //递归步骤
}
试推导求n!时的计算次数。
为推导求n!时的计算次数,可用递归方式计算。设当n=0时计算时间复杂度为常数T(0)=d,当n>0时按T(n)=T(n-1)+c(c为常数),则有:
T(n)=T(n-1)+c=T(n-2)+2×c=T(n-3)+3×c=…=T(1)+(n-1)×c
=T(0)+n×c=n×c+d
2. 定义斐波那契数列为F
0=0,F
1=1,F
i=Fi
-1+F
i-2,i=2,3,…,n。其计算过程为
Long Fib (long n){
if (n<2) return (n);
else return (Fib (n-1)+Fib (n-2));
}
试推导求F
n时的计算次数。
为推导求F
n时的计算,此时,以n=5为例,求Fib(5)的递归树如下图所示。
Fib(5)的递归树
计算Fib(5)要计算1次Fib(4),2次Fib(3),3次Fib(2),5次Fib(1),3次Fib(0)。总的递归调用次数达到15次,递归深度达到5层。一般清晰的总调用次数为
设计算Fib(0)的时间为T(0)=1,计算Fib(1)的时间为T(1)=1,计算Fib(i)的时间为T(i)=T(i-1)+T(i-2)+1。由此可推导之:
T(2)=T(1)+T(0)+1=3,T(3)=T(2)+T(1)+1=5,T(4)=T(3)+r(2)+1=9,…。
符合上面的计算公式。
3. 试推导当总盘数为n时的Hanoi塔的移动次数。
描述Hanoi塔问题的递归算法如下:
void Hanoi (int n,char x,char y,char z){
if (n==1)move(x,1,z);
else{
Hanoi (n-1,x,z,y);
move (x,1,z);
Hanoi (n-1,y,x,z);
}
}
设move()函数执行的移盘次数为常数1,则Hanoi塔问题总的运算次数为:
T(1)=1;
T(2)=2×T(1)+1=3=22-1;
T(3)=2×T(2)+1=2×3+1=7=23-1;
T(4)=2×T(3)+1=2×7+1=15=24-1;
…
T(n)=2×T(n-1)+1=2n-1
QUEUE:(设定每个队列元素的数据类型为Type)
bool isEmpty(QUEUE Q); //判断队列空否,true为空,false不空
bool getFront(QUEUE Q,Type&x); //通过x返回队头元素的值
void enQueue(QUEUE Q,Type x); //将新元素x插入到队列的队尾
void deQueue(Queue Q); //从队列中退出队头元素
STACK:(设定每个栈元素的数据类型与队列相同,为Type)
void initStack(STACK S); //对新创建的栈初始化,置成空栈
bool isEmpty(STACK S); //判断栈空否,true栈空,false不空
void push(STACK S,Type x); //将新元素X进栈
void pop(STACK S); //栈顶元素退栈
bool getTop(STACK S,Type&x); //通过x返回栈顶元素的值
利用以上栈和队列的操作,编写以下针对队列的函数的实现代码(要求非递归实现)。4. “逆转”函数void reverse(QUEUE&Q)
利用队列和栈实现以下算法(要求非递归实现)。
“逆转”函数。将队列中全部元素出队并放进栈里,这样所有元素排列的顺序颠倒。再把栈里的所有元素退出栈并放进队列中,所有元素的排列顺序与当初它们在队列中的排列顺序全部逆转了。
void reverse (QUEUE&Q){
STACK S;initStack (s);Type trap;
while (!isEmpty(Q)) {getFront(Q,tmp);deQueue(Q);Push(S,tmp);}
while (!isEmpty(S)) {getTop(S,tmp);Pop(S);enQueue(Q,tmp);}
}
5. “判等”函数bool equal(QUEUE Q1,QUEUE Q2)
“判等”函数。本函数做判等比较,所以判断之后,原队列的内容应保持比较之前的状态,不能因判断而改变,所以函数参数表中的两个队列应是传值型参数,不应是引用型参数,Q1和Q2是实际参数的副本。算法思路是:当两个队列都非空时,做对应元素比较,一旦发现不等则立即可以断定两个队列不等并退出比较,否则继续比较。当两个队列经过这样的逐个元素比较后都变空且每一对应元素都相等,则两个队列相等;否则不等。
bool equal (QUEUE Q1,QUEUE Q2){
Type t1,t2;bool finished=true;
while (!is.Empty(Q1)&&! is.Empty(Q2)){
getFront(Q1,t1);deQueue(Q1); //从左队列退出一个元素
getFront(Q2,T2);deQueue(Q2); //从右队列退出一个元素
if(t1!=t2){finished=false;break;}
}
if(finished==false ||!isEmpty(Q1)}||!isEmpty(Q2))return false;
else return true;
}
6. “清空”函数void clear(QUEUE&Q);
“清空”函数。算法思路是:当队列不空时逐个退出队列中的元素。
void clear (QUEUE&Q){
while (!isEmpty (Q))deQueue(Q);
}
7. 借助栈实现带表头结点的单链表上的逆置运算。
由于进栈与出栈顺序正好相反,因此,借助栈可以实现单链表的逆置运算。方法是让单链表中的结点依次进栈,再依次出栈。
void invert(LinkList &L){ //使用引用型参数可不必创建L的副本
Stack S;LinkedNode*p=L->link,*q;
while (p!=NULL) {push(s,p);p=p->link;} //依次将链中结点进栈
p=L; //p起到单链表尾指针作用
while (!isEmpty(S)){ //将栈中保存的结点依次出栈
pop (S,q);p->link=q; //出栈元素链入逆置后的链中
p=p->link; //p进到链表尾结点
}
p->link=NULL; //逆置后的链表收尾
}
8. 编写一个算法,将一个非负的十进制整数N转换为一个二进制数。
可以利用栈解决数制转换问题,将一个非负的十进制整数Ⅳ转换为一个二进制数。例如:49
10=1·2
5+1·2
4+1·2
0=110001
2,
99
10=1·2
6+1·2
5+0·2
4+0·2
3+0·2
2+1·2
1+1·2
0=1100011
2。
其转换规则是:
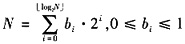
其中,b
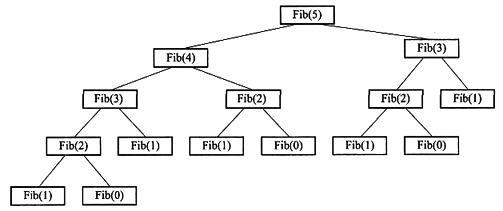
i表示二进制数的第i位上的数字。这样,十进制数N可以用长度为
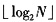
+1位的二进制数表示为
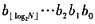
。若令
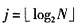
,则有
N=b
j2
j+6
j-12
j-1+…+b
12
1+b
0 =(b
j2
j-1+b
j-12
j-2+…+b
1)×2+b
0=(N/2)×2+N%2(“/”表示整除运算)
因此,可以先通过N%2救出b
0,然后令N=N/2,再对新的N做除2求模运算可求出b
1,如此重复直到某个N等于零结束。这个计算过程是从低位到高位逐个进行的,但输出过程是从高位到低位逐个打印的,为此需要利用栈来实现。
int BaseTrans (int N){
int i,result=0;Stack S;
while (N!=0) {i=N%2;N=N/2;push(S,i);}
while (!isEmpty(S)){
pop (S,i);result=result*10+i;
}
return result;
}
9. 试编写一个算法,检查一个程序中的花括号、方括号和圆括号是否配对,若能够全部配对则返回1,否则返回0。
在算法中,扫描程序中的每一个字符,当扫描到花、中、圆左括号时,令其进栈,当扫描到花、中、圆右括号时,则检查栈顶是否为相应的左括号,若是则作退栈处理,若不是则表明出现了语法错误,应返回0。当扫描到程序文件结尾后,若栈为空则表明没有发现括号配对错误,应返回1,否则表明栈中还有未配对的括号,应返回0。另外,对于一对单引号或双引号内的字符不进行括号配对检查。
根据分析,编写出算法如下:
int BracketsCheck (char*f){
//对由f所指字符串中的文本进行括号配对检查
stack S;char ch; //定义一个栈
char*p=f;
while(*p!='\0'){ //顺序扫描字符串中的每一个字符
if (*p==39){ //单引号内的字符不参与配对比较
while (*p!='\0'&&'P!=39) //39为单引号的ASCII值、p++;
}
else if(*p!='\0'&&*p==34){ //双引号内的字符不参与配对比较
while(*p!='\0'&&*p!=34) //34为双引号的ASCII值p++;
}
if (*p!='\0'){
switch (*p){
case'{':case'[':case'(':push(S,*p);break; //左括号进栈
case'}':getTop(S,ch);
if(ch=='{')pop(S,ch); //栈顶的左花括号出栈
else return(0);break;
case']':getTop(S,ch);
if(ch=='[')pop(S,ch); //栈顶的左中括号出栈
else return(0);break;
case')':getTop (S,ch);
if (ch=='(')pop (S,ch); //栈顶的左圆括号出栈
else return(0);
}
p++;
}
if (isEmpty(S)) return (1);
else return (0);
}
}
10. 将表达式的中缀表示转换为相应的后缀表示时,需要利用栈暂存某些操作符,现有一个表达式的中缀表示:
a+b*(c-d)+e/f#
请给出转换为后缀表示时的处理过程及栈的相应变化。
※提示:运算符的优先级如下表所示,其中,icp表示当前扫描到的运算符ch的优先级,该运算符进栈后的优先级为isp,字符“#”为表达式结束符。
| 运算符 | # | ( | *,/ | +,- | ) |
| isp | 0 | 1 | 5 | 3 | 6 |
| icp | 0 | 6 | 4 | 2 | 1 |
表达式的中缀表示:a+b*(c-d)+e/f#转换为相应的后缀表示时,需要利用栈暂存某些操作符。如下表所示。
| 步序 |
扫描项 |
项类型 |
动作 |
栈的变化 |
输出 |
| 0 |
|
|
'#'进栈,读下一符号 |
# |
|
| 1 |
a |
操作数 |
直接输出,读下一符号 |
# |
a |
| 2 |
+ |
操作数 |
isp('#')<icp('+'),进栈,读下一符号 |
#+ |
|
| 3 |
b |
操作数 |
直接输出,读下一符号 |
#+ |
b |
| 4 |
* |
操作数 |
isp('+')<icp('*'),进栈,读下一符号 |
#+* |
|
| 5 |
( |
操作数 |
isp('+')<icp('('),进栈,读下一符号 |
#+*( |
|
| 6 |
c |
操作数 |
直接输出,读下一符号 |
#+*( |
c |
| 7 |
- |
操作数 |
isp('(')<icp('-'),进栈,读下一符号 |
#+*(- |
|
| 8 |
d |
操作数 |
直接输出,读下一符号 |
#+*(- |
d |
| 9 |
) |
操作数 |
isp('-')>icp(')'),退栈输出 |
#+*( |
- |
| 10 |
|
|
Isp('(')==icp(')'),退栈,读下一符号 |
#+* |
|
| 11 |
+ |
操作数 |
isp('*')>icp('+'),退栈输出 |
#+ |
* |
| 12 |
|
|
isp('+')>icp('+'),退栈输出 |
#+ |
+ |
| 13 |
|
|
isp('#')<icp('+'),进栈,读下一符号 |
#+ |
|
| 14 |
e |
操作数 |
直接输出,读下一符号 |
#+ |
e |
| 15 |
/ |
操作数 |
isp('+')<icp('/'),进栈,读下一符号 |
#+/ |
|
| 16 |
f |
操作数 |
直接输出,读下一符号 |
#+/ |
f |
| 17 |
# |
操作数 |
isp('/')>icp('*'),退栈输出 |
#+ |
/ |
| 18 |
|
|
isp('+')>icp('#'),退栈输出 |
# |
+ |
| 19 |
|
|
isp('#')==icp('#'),退栈,结束 |
|
|
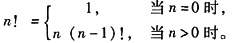
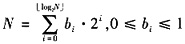
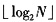 +1位的二进制数表示为
+1位的二进制数表示为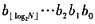 。若令
。若令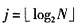 ,则有
,则有