综合应用题一棵高度为h的满m叉树有如下性质:第h层上的结点都是叶结点,其余各层上每个结点都有m棵非空子树。如果按层次自顶向下,同一层自左向右,顺序从1开始对全部结点进行编号,试问:1. 各层的结点个数是多少?
可以参照二叉树的性质,将其扩展到m叉树。
因为第1层有1个结点,第2层有m个结点,第3层有m2个结点……一般地,第i层有mi-1个结点(1≤i≤h)。
2. 编号为i的结点的父结点(若存在)的编号是多少?
在m叉树的情形,结点i的第1个子女编号为j=(i-1)×m+2。反过来,结点i的双亲的编号是
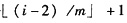
,根结点没有双亲,所以以上计算式要求i>1。如果考虑对于i=1也适用(根的双亲设为0),可将上式改为
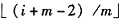
。
3. 编号为i的结点的第k个子女结点(若存在)的编号是多少?
因为结点i的第1个子女编号为(i-1)×m+2,若设该结点子女的序号为k=1,2,…,m,则第k个子女结点的编号为(i-1)×m+k+1(1≤k≤m)。
4. 编号为i的结点有右兄弟的条件是什么?其右兄弟结点的编号是多少?
当结点i不是其双亲的第m个子女时才有右兄弟。若设其双亲编号为j,可得j=
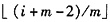
,结点j的第m个子女的编号为:(j-1)×m+m+1=j×m+1
所以当结点的编号i≤j×m时才有右兄弟,右兄弟的编号为i+1。
5. 若结点个数为n,则高度h是n的什么函数关系?
若结点个数为n,则有

反之,有h=logm(n×(m-1)+1)。
6. int size(BiTNode
*t); //返回以
*t为根的二叉树中所有结点个数
返回以*t为根的二叉树中所有结点个数:
int size(BinTreeNode*t){
if(t==NULL)return 0;
return 1+size(t->lchild)+size(t->rchild);
}
7. int leaves(BiTNode
*t); //返回以
*t为根的二叉树的叶结点个数
返回以*t为根的二叉树中叶结点个数:
int leayes(BiTNode*t){
if(t==NULL) return 0;
if(t->lchild==NULL&&t->rchild==NULL)return 1;
return leayes(t->lchild)+leayes(t->rchild);
}
8. int height(BiTNode
*t); //返回以
*t为根的二叉树的高度
返回以*t为根的二叉树的高度:
int height(BiTNode*t){
if(t==NULL)return 0;
int h1=height(t->lchild);
int hr=height(t->rchild);
if(h1>hr)return h1+1;
else return hr+1;
}
9. int level(BiTNode
*t,BiTNode
*p);//返回二叉树指定结点
*p在以
*t为根的子树中的层次
返回以*t为根的二叉树中指定结点*p所在层次:
int level(BiTNode*t,BiTNode*p,int d){
if(t==NULL) return 0;
if(t==p) return(d);
int level;
if(level=level (t->lchild,p,d+1))
return (level1);
else return (level (t->rchild,p,d+1));
}
10. void reflect(BiTNode
*t); //交换以
*t为根的二叉树中每个结点的两个子女
交换以*t为根的二叉树中每个结点的两个子女:
void reflect(BiTNode*t){
if(t==NULL)return;
reflect(t->lchild);
reflect(t->rchild);
BiTNode*p=t->lchild;t->lchiId=t->rchild;t->rchild=p;
}
11. void defoliate(BiTNode
*&t); //从以
*t为根的二叉树中删去所有叶结点
从以*t为根的二叉树中删去所有叶结点:
void defoliate(BiTNode*&t){
if(t==NULL)return;
if(t->lchild==NULL&&t->rchild==NULL){free(t);t=NULL;}
else{
defoliate(t->lchild);
defoliate(t->rchild);
}
}
12. 已知一棵二叉树的前序遍历序列为ABECDFGHIJ,中序遍历序列为EBCDAFHIGJ,试画出这棵二叉树并写出它的后序遍历序列。
当前序序列为ABECDFGHU,中序序列为EBCDAFHIGJ时,逐步形成二叉树的过程如下图所示。
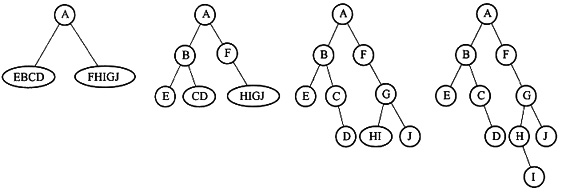
其后序遍历序列为EDCBIHJGFA。
13. 深度为d的完全二叉树的不同二叉树棵数。
深度为d的完全二叉树的1到d-1层都是满的,第d层有多少结点就有多少种选择。第d层最多有2d-1个结点,所以不同二叉树的棵数有2d-1棵。
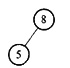
15. 画出一个二叉树,使得它既满足大根堆的要求又满足二叉排序树的要求。
大根堆要求根结点的关键字值既大于或等于左子女的关键字值又大于或等于右子女的关键字值,二叉排序树要求根结点的关键字值大于左子女的关键字值同时小于右子女的关键字值。两种的交集是:根结点的关键字值大于左子女的关键字值。这意味着是一棵左斜单枝树。但大根堆要求其是完全二叉树,因此最好得到的是如下图所示的只有两个结点的二叉树。
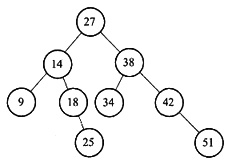
16. 给定一个关键字集合{25,18,34,9,14,27,42,51,38},假定查找各关键字的概率相同,请画出其最佳二叉排序树。
当各关键字的查找概率相等时,最佳二叉排序树应是高度最小的二叉排序树。构造过程分两步走:首先对各关键字值从小到大排序,然后仿照折半查找的判定树的构造方法构造二叉排序树。这样得到的就是最佳二叉排序树,如下图所示。
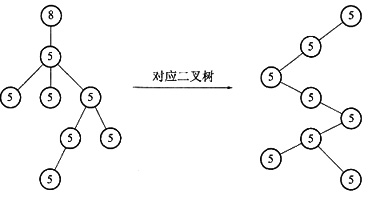
17. 利用树的先根遍历结果和后根遍历结果能否唯一确定一棵树?举例说明。
因为给出二叉树的前序遍历序列和中序遍历序列能够唯一地确定这棵二叉树,因此,根据题目给出的条件,利用树的先根次序遍历结果和后根次序遍历结果能够唯一地确定一棵树。例如,对于下图中左图所示的树,对应二叉树的前序序列为1,2,3,4,5,6,8,7,中序序列为3,4,8,6,7,5,2,1。原树的先根遍历序列为1,2,3,4,5,6,8,7,后根遍历序列为3,4,8,6,7,5,2,1。
18. n个结点的不同形状的树有多少种?
确定n个结点的不同树的数目可以归结到确定其对应二叉树的计数。因为树转化为二叉树后,根结点没有右子女,该二叉树的计数归结到对应二叉树根下左子树可能有多少种不同构造。可以利用n-1个结点的catalan函数来计算。
void PreOrder(BiTNode*t){
if(t!=NULL){ //递归结束条件
cout<<t->data; //访问(输出)根结点
Preorder(t->lchild); //前序遍历根的左子树
Preorder(t->rchild); //前序遍历根的右子树
}
}19. 改写PreOrder算法,消去第二个递归调用PreOrder(t->rchild);
消去第二个递归语句时,视第一个递归语句为一般语句,按尾递归处理。
void preOrder(BiTNode*t) {
while(t!=NULL){ //按尾递归改为循环
cout<<t->data;
PreOrder(t->lchild);
t=t->rchild; //向右子树循环
}
}
20. 利用栈改写PreOrder算法,消去两个递归调用。
定义一个栈,在访问某一个结点时保存其右、左子女结点的地址。下一步将先从栈中退出右子女结点,对其进行遍历,然后从栈中退出左子女结点,对其进行遍历。
void PreOrder(BiTNode*t){
BiTNode*p;
Stack S;initStack(S);push(S,t);
while (!IsEmpty(s)){
pop (S,p);
cout<<p->data;
if(p->rchild!=NULL)push(S,p->rchild);
if(p->lchild!=NULL)push(S,p->ichild);
}
}
21. 有n个顶点的有向强连通图最多有多少条边?最少有多少条边?
有n个顶点的有向强连通图最多有n(n-1)条边,最少有n条边。
22. 表示一个有1000个顶点、1000条边的有向图的邻接矩阵有多少个矩阵元素?是否为稀疏矩阵?
有1000个顶点、1000条边的有向图的邻接矩阵有1000000个矩阵元素,其中只有1000个非零元素,是一个稀疏矩阵。注意,它不一定是对称的。
23. 对于一个有向图,不用拓扑排序,如何判断图中是否存在环?
对一个有向图,还可以用以下方法判断图中是否存在环:①如果图中所有顶点的出度至少为1,入度也至少为1,则图中存在环。这个条件太强。②如果对图进行深度优先搜索,从某个顶点出发,又走到以前已经访问过的顶点,则图中存在环。
24. 在有关图的算法中常用到两个图的操作:
int getFirstNeighbor (Graph G,int v); //取顶点v的第一个邻接顶点
int getNextNeighbor(Graph G,int v,int w); //取邻接顶点w的下一邻接顶点
试分别给出在邻接矩阵和邻接表为存储结构的情形下它们的实现。
(1)用邻接矩阵做存储结构的场合。
为了找到顶点v的第一个临界顶点,顺序地检测邻接矩阵的第v行,最先遇到的非零元素(带权图情形是小于maxValue的元素)就是顶点v的第一个邻接顶点。从这个矩阵元素继续向后找,就可以以类似的判断找到下一个邻接顶点。
int getFirstNeighbor(Graphmtx&G,int v){
//给出顶点v的第一个邻接顶点,如果找不到,则函数返回-1。
if(v!=-1){
for(int col=0;col<G.numvertices;col++)
if(G.Edge[v][col]>0&&G.Edge[v][col]<maxValue)return col;
}
return-1;
}
int getNextNeighbor(Graphmtx &G,int v,int w){
//给出顶点v的某邻接顶点w的下一个邻接顶点
if(v!=-1&&w!=-1){
for(int col=w+1;col<G.numVertices;col++)
if(G.Edge[v][col]>0&&G.Edge[V][col]<maxWeight)return col;
}
return-1;
}
(2)用邻接表作存储结构的场合。
为了找到顶点v的第一个邻接顶点,检测邻接表第v个边链表,如果链表非空,第一个边结点中dest域存放的顶点(号)就是顶点v的第一个邻接顶点。在此链表中该边结点的下一个边结点就是下一个邻接顶点。
int getFirstNeighbor(Graphlnk&G,int v){
//给出顶点v的第一个邻接顶点,如果找不到,则函数返回-1。
if(v!=-1){ //顶点v存在
Edge*p=G.NodeTable[v].adj; //对应边链表第一个边结点
if(p!=NULL)return p->dest; //存在,返回第一个邻接顶点
}
Return-1; //第一个邻接顶点不存在
}
int getNextNeighbor(Graphlnk&G,int v,int w) {
//给出顶点v的邻接顶点W的下一个邻接顶点,如果找不到,则函数返回-1。
if(v!=-1){ //顶点v存在
Edge*p=G.NodeTable[v].adj; //对应边链表第一个边结点
while (p!=NULL&&p->dest!=w)p=p->link; //寻找邻接顶点w
if (p!=NULL&&p->link!=NULL)return p->link->dest;
//返回下一个邻接顶点
}
return-1; //下一邻接顶点不存在
}
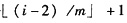 ,根结点没有双亲,所以以上计算式要求i>1。如果考虑对于i=1也适用(根的双亲设为0),可将上式改为
,根结点没有双亲,所以以上计算式要求i>1。如果考虑对于i=1也适用(根的双亲设为0),可将上式改为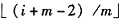 。
。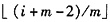 ,结点j的第m个子女的编号为:(j-1)×m+m+1=j×m+1
,结点j的第m个子女的编号为:(j-1)×m+m+1=j×m+1




