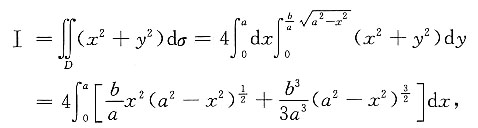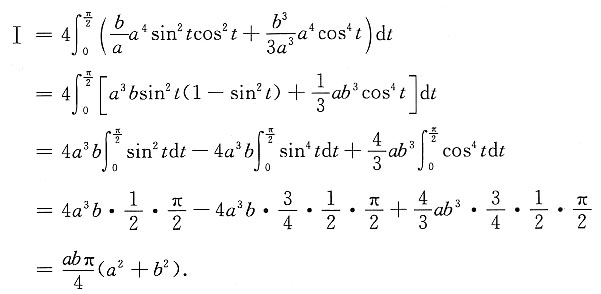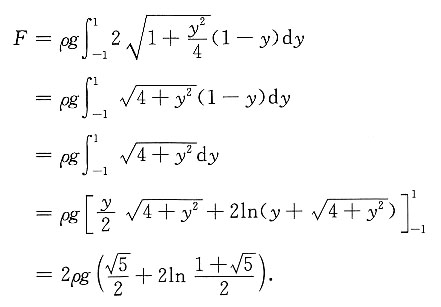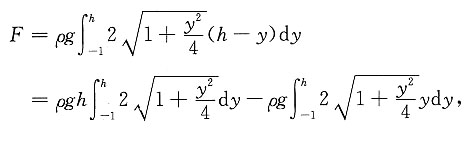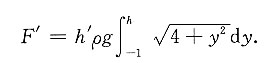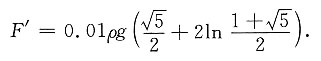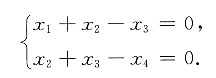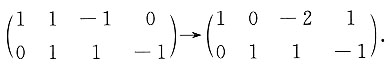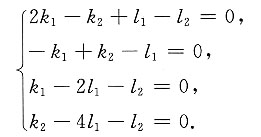一、选择题1. 设g(x)在区间(-∞,+∞)内具有连续的一阶导数且g'(x)>0,并设
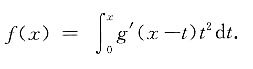
则
- A.f(0)是f(x)的极大值.
- B.f(0)是f(x)的极小值.
- C.曲线y=f(x)在区间(-∞,0)上是凹弧,在(0,+∞)上是凸弧.
- D.曲线y=f(x)在区间(-∞,0)上是凸弧,在(0,+∞)上是凹弧.
A B C D
D
[解析]
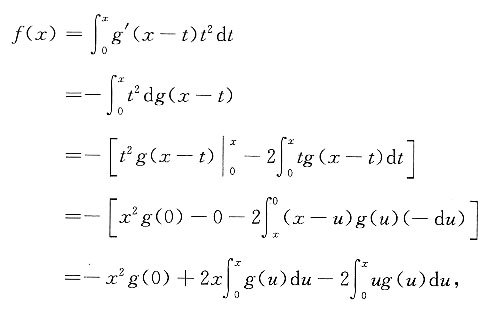

其中由积分中值定理知,ξ介于0与x之间.再进一步,
g(ξ)-g(0)=g'(η)ξ,
其中η介于0与ξ之间.
由于ξ与x同号,所以当x≠0时,
f'(x)=2xξg'(η)>0.
不选A,也不选B.再求
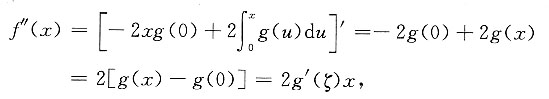
其中ζ介于0与x之间.由上式知,当x<0时f"(x)<0,当x>0时f"(x)>0.选D.
2. 当x→0时,下列4个无穷小量关于x的阶数最高的是
A.x
2+x
4.
B.
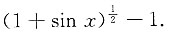
C.
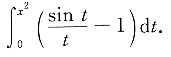
D.
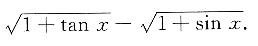
A B C D
C
[解析] 当x→0时,
A.x
2+x
4~x
2.
B.

C.
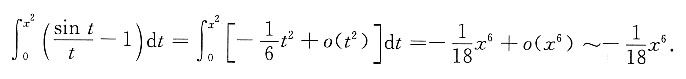
D.
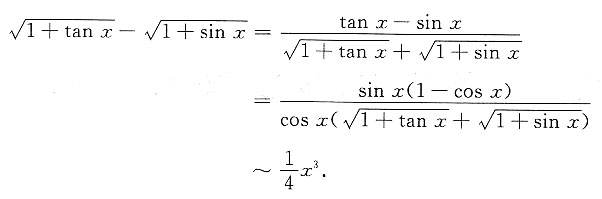
3. 下列反常积分收敛的是
A.
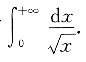
B.
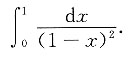
C.
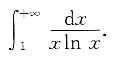
D.
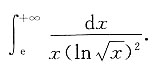
A B C D
D
[解析]

通过具体计算,可知A、B、C均发散.
4. 由曲线
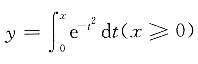
和其水平渐近线

以及y轴所围区域的面积A为
A.
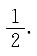
B.
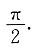
C.
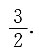
D.
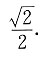
A B C D
A
[解析]
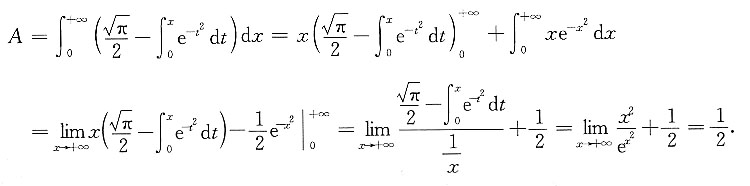
5. 船航行每小时的费用由两个部分组成.日常开销(固定部分)为k
1,燃油费(变动部分)与速度立方成正比,比例系数k
2>0.在航程确定的情况下,使船航行总费用最小的航速为
A.
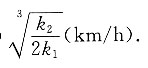
B.
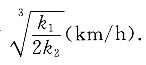
C.

D.
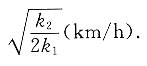
A B C D
B
[解析] 航行总费用y与航速vkm/h有关,设航程为skm,则航行时间为
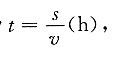
所以有
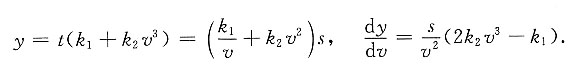
当

时,
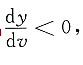
y单调递减;
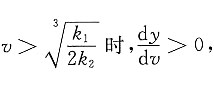
y单调递增.
所以
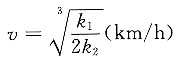
时,航行总费用最省.
6.

A.e
B.2e.
C.
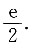
D.e
2.
A B C D
C
[解析]
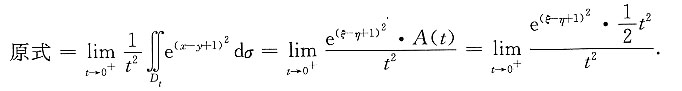
其中(ξ,η)∈D
t,D
t={(x,y)|t≤x≤2t,t≤y≤x),A(t)为D
t的面积.
由于t→0
+时,有D
t→(0,0),所以(ξ,η)→(0,0),

7. 设α
1,α
2,α
3,α
4是4个4维非零列向量,A=(α
1,α
2,α
3,α
4).且AX=0的通解为
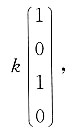
k为任意常数,则以下5个向量组,
①α
1,α
2,α
3; ②α
1+α
2,α
2+α
3,α
3+α
1; ③α
1+α
2,α
2+α
3,α
3+α
4,α
4+α
1;
④α
2,α
3,α
4; ⑤α
1,α
2,α
4,
可作为A
*X=0的基础解系的向量组的个数为
A B C D
B
[解析] 首先,由AX=0的通解结构,知r(A)=3,故r(A
*)=1,于是A
*X=0的基础解系中有3个向量,排除③;
又由A*A=|A|E=0,知α
1,α
2,α
3,α
4均为A*X=0的解,且α
1+α
3=0,于是α
1,α
2,α
3线性相关,排除①;再看②,
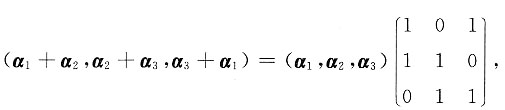
故r(α
1+α
2,α
2+α
3,α
3+α
1)≤r(α
1,α
2,α
3)<3,排除②;
最后看④、⑤,由于r(A)=3,故α
1,α
2,α
3,α
4中存在3个线性无关的向量,又α
1+α
2=0,即α
1,α
2,α
3;α
1,α
3,α
4均线性相关,而④α
2,α
3,α
4与⑤α
1,α
2,α
4必都线性无关,否则就不存在3个线性无关的向量了,故④、⑤均符合题意,答案选择B.
8. 设矩阵
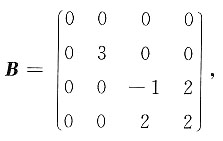
矩阵A~B,则秩r(A-E)+r(A-3E)=
A B C D
A
[解析] 由矩阵B的特征多项式

可得B的特征值为λ
1=0,λ
2=-2,λ
3=λ
4=3.
因为A~B,所以矩阵A与矩阵B有相同的特征值.又因为B是实对称矩阵,故B可相似于对角矩阵.
从而,矩阵A也可相似于对角矩阵.所以,矩阵A的2重特征值λ
3=λ
4=3,必有2个线性无关的特征向量.
由此可知,r(3E-A)=n-2=4-2=2,即r(A-3E)=2.又因为λ=1不是矩阵A的特征值,故知|E-A|≠0.所以,r(E-A)=4,即r(A-E)=4.因此,
r(A-E)+r(A-3E)=4+2=6.
二、填空题1. 设常数a≠2.函数
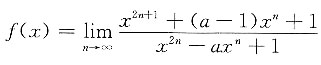
在区间(0,+∞)上连续的充要条件是a=______.
[解析] 当0<x<1时,f(x)=1;当x=1时,
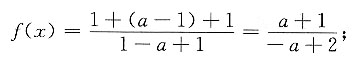
当x>1时,
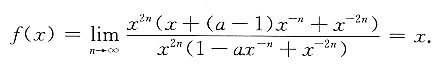
在x=1处连续的充要条件是
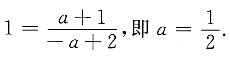
而在x>0的其它处,无论a取什么值,f(x)总是连续的.所以f(x)在(0,+∞)上连续的充要条件是
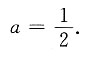
2. 设常数a>0,b>0.则
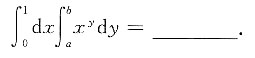
[解析] 交换积分次序
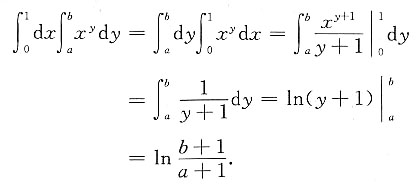
3. 设存在二元可微函数u(x,y),
du(x,y)=(axy
3-y
2cos x)dx+(1+bysin x+3x
2y
2)dy,
则常数a=______,b=______,函数u(x,y)=______.
2;-2;x2y3-y2sin x+y+C(其中C是任意常数)
[解析] 由题给条件知,
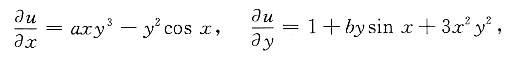
于是有
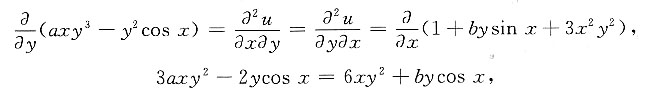
所以a=2,b=-2.于是
du(x,y)=(2xy
3-y
2cosx)dx+(1-2ysin x+3x
2y
2)dy
=(2xy
3dx+3x
2y
2dy)-(y
2cosxdx+2ysin xdy)+dy
=d(x
2y
3)-d(y
2sin x)+dy
=d(x
2y
3-y
2sin x+y),
所以u(x,y)=x
2y
3-y
2sinx+y+C(其中C是任意常数).
4. 设
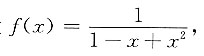
则f
(2 016)(0)=______.
2 016!
[解析] 注意,f(x)的分母不能因式分解而将f(x)拆项,改想别的办法.
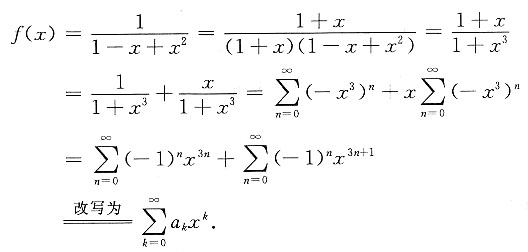
由幂级数展开式的唯一性知
f
(k)(0)=k!a
k (k=0,1,2,…).
当k=2 016时,3n=2 016,n=672.所以
f
(2 016)(0)=2 016!a
2 016=2 016!(-1)
672=2 016!
5. 微分方程y"+4y=2x
2在原点处与直线y=x相切的特解为______.
[解析] 由题意,在原点处切线的斜率为y'|
x=0=1,且y|
x=0=0. ①
特征方程r
2+4=0,对应齐次微分方程的通解为C
1 cos 2x+C
2 sin 2x.
又微分方程的一个特解为
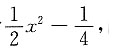
因而非齐次方程的通解为
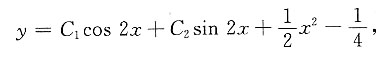
将①代入上式,得特解为
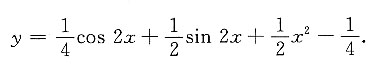
6. 设实二次型f(x
1,x
2,x
3)=x
TAx经正交变换化成的标准形为
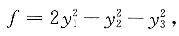
A
*是A的伴随矩阵,且向量α=(1,1,-1)
T满足A*α=α,则二次型f(x
1,x
2,x
3)=______.
2x1x2-2x1x3-2x2x3
[解析] 由于A的特征值为2,-1,-1,所以|A|=2×(-1)×(-1)=2.
对A*α=α两边左乘A,并利用AA'=|A|E得Aα=2α.这表明α是A的对应于特征值2的特征向量.
取α
2=(0,1,1)
T,α
3=(-2,1,-1)
T,则α,α
2,α
3两两正交,将它们分别单位化,
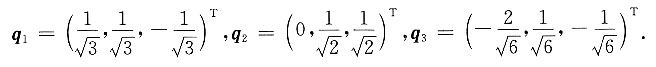
令Q=(q
1,q
2,q
3),即Q为正交矩阵,且
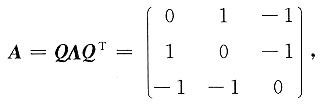
所以二次型f(x
1,x
2,x
3)=2x
1x
2-2x
1x
3-2x
2x
3.
三、解答题1. 设函数z=z(x,y)是由方程
x
2-6xy+10y
2-2yz-z
2+32=0
确定,讨论函数z(x,y)的极大值与极小值.
[解] 将x
2-6xy+10y
2-2yz-z
2+32=0两边分别对x、对y求偏导数,有

为求驻点,令
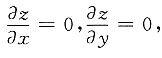
联立方程得

再与原设方程
x
2-6xy+10y
2-2yz-z
2+32=0
联立解得点(12,4,4)
1与(-12,-4,-4)
2.再将(*)与(**)对x、对y求偏导数,得
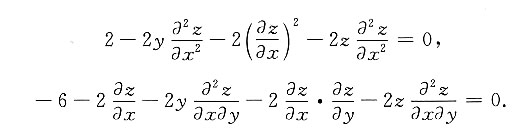
及
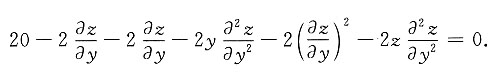
再以

点(12,4,4)
1代入得
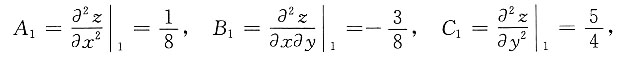
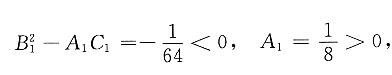
所以z=4为极小值.
点(-12,-4,-4)
2代入得
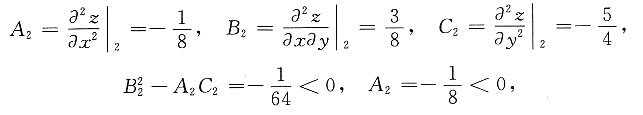
所以z=-4为极大值.
2. 设x<1且x≠0.证明:
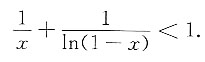
[证]
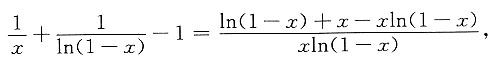
当0<x<1时,xln(1-x)<0;当x<0时仍有xln(1-x)<0.
为证
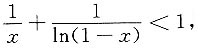
等价于证明,当x<1且x≠0时
ln(1-x)+x-xln(1-x)>0.
令 f(x)=ln(1-x)+x-xln(1-x),f(0)=0,
有
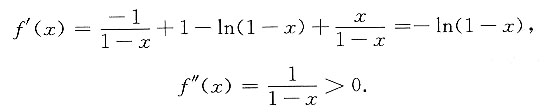
f'(0)=0,f"(0)=1>0,所以f(0)=0是f(x)的唯一极小值,是最小值,所以当x<1时f(x)≥0且仅当x=0时f(x)=0.证毕.
3. 若函数f(x)在[a,b]上连续,证明:
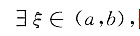
使得
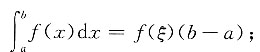
[证] 令
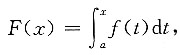
则F(x)在[a,b]上满足拉格朗日中值定理的条件.
故
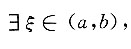
使得
F(b)-F(a)=F'(ξ)(b-a),
即
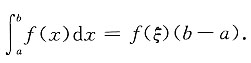
4. 计算
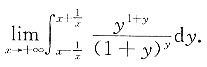
[解] 由于
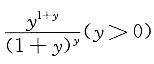
是连续的,由积分中值定理,存在
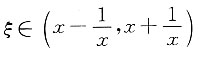
(x>0),使

由于
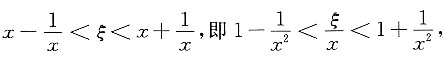
而在x→+∞时,有
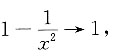
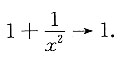
由夹逼定理可知,x→+∞时,
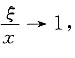
且有ξ→+∞,故
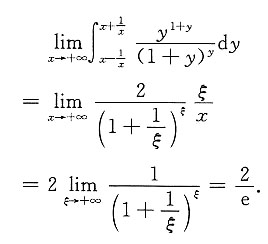
5. 设曲线y=y(x)在
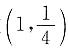
点与直线4x-4y-3=0相切,且y=y(x)满足方程
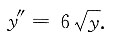
求该曲线在相应x∈[-1,1]上点(x,y)处的曲率.
[解] 令p=y',由
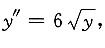
得
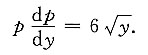
解得
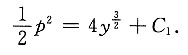
由
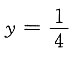
时,p=1,得C
1=0.从而
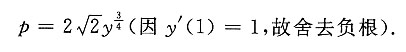
解得

在(x,y)点的曲率
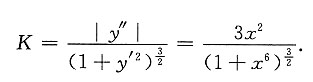
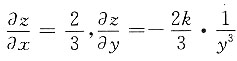 (k是正常数),且
(k是正常数),且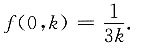
7.
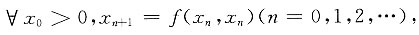
证明:数列{x
n}收敛,并求
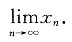
[证] 由题知
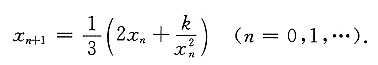
由x
0>0及k>0知x
n>0(n=1,2,…).故
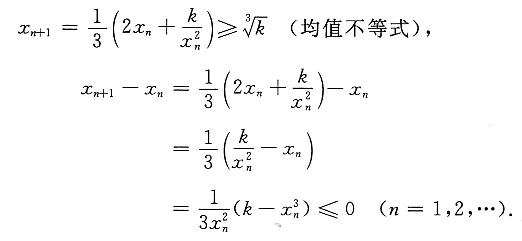
因此,{x
n}单调递减有下界,故数列收敛.
设
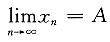
得
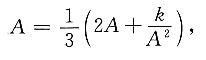
求得
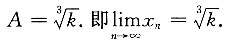
8. 设平面区域
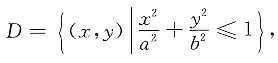
其中常数a>0,b>0,求二重积分

[解] 用直角坐标.由对称性,
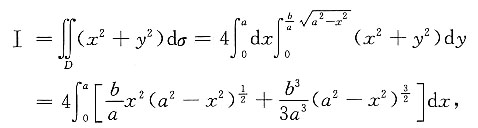
作积分变量变换,令x=asin t,
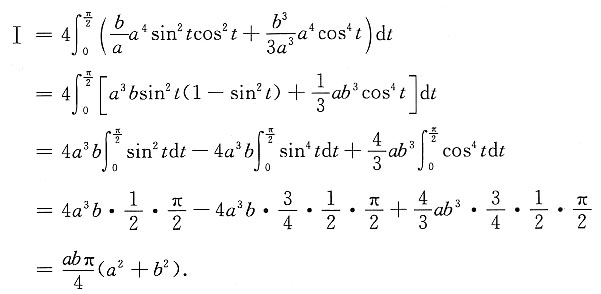
9. 如果平板的上边缘与水面相齐,那么平板一侧所受到的总压力是多少?
[解] 平板的上边缘与水面相齐,那么平板一侧所受到的总压力为
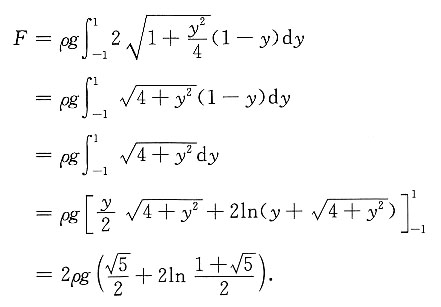
10. 设水位下降,如果在时刻t时水面位于y=h(t)处,且水面匀速下降速率为0.01(m/s).问:当水面下降至平板的中位线时,一侧所受到的水压力的下降速率是多少?
[解] 水面位于y=h(t)处,水压力为
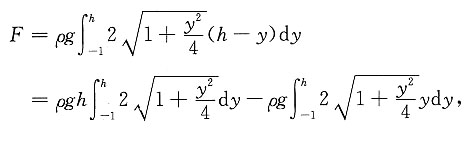
则水压力的下降速率为
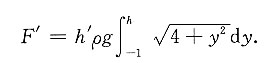
由题意知h'=0.01,当水面下降至平板的中位线时,h=0,代入上式得
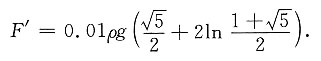
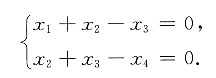
齐次线性方程组(ii)的基础解系为
ζ1=(-1,1,2,4)T,ζ2=(1,0,1,1)T.11. 求方程组(i)的基础解系;
[解] 对齐次线性方程组(i)的系数矩阵作初等行变换,得
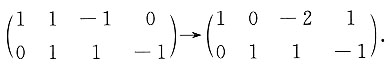
其同解方程组为

由此解得方程组(i)的基础解系为
η
1=(2,-1,1,0)
T,η
2=(-1,1,0,1)
T.
12. 求方程组(i)与(ii)的全部非零公共解,并将非零公共解分别由方程组(i),(ii)的基础解系线性表示.
[解] 由上题解得方程组(i)的基础解系η
1,η
2.于是,方程组(i)的通解为
k
1η
1+k
2η
2=k
1(2,-1,1,0)
T+k
2(-1,1,0,1)
T (k
1,k
2为任意常数).
由题设知,方程组(ii)的基础解系为ξ
1,ξ
2,其通解为
l
1ξ
1+l
2ξ
2=l
1(-1,1,2,4)
T+l
2(1,0,1,1)
T (l
1,l
2为任意常数).
为求方程组(i)与(ii)的公共解,令它们的通解相等,即
k
1(2,-1,1,0)
T+k
2(-1,1,0,1)
T =l
1(-1,1,2,4)
T+l
2(1,0,1,1)
T.
从而,得到关于k
1,k
2,l
1,l
2的方程组
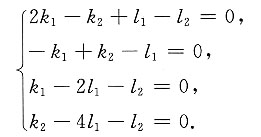
对此方程组的系数矩阵作初等行变换,得
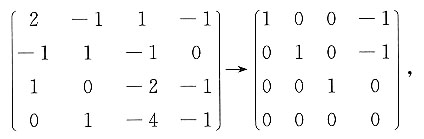
由此可得,k
1=k
2=l
2,l
1=0.
所以,令k
1=k
2=k,方程组(i),(ii)的非零公共解是
k(2,-1,1,0)
T+k(-1,1,0,1)
T=k(1,0,1,1)
T(k为任意非零常数).
并且,方程组(i),(ii)的非零公共解分别由方程组(i),(ii)的基础解系线性表示为
k(η
1+η
2)和0·ξ
1+kξ
2.
13. 若A、B均为n阶矩阵,且A
2=A,B
2=B,r(A)=r(B),证明:A、B必为相似矩阵.
[证] 由A2=A,可知A的特征值为0或1,对应于0、1的线性无关的特征向量的个数
分别为n-r(0·E-A)与n-r(1·E-A).
又由于A2-A=0,即A(A-E)=0,则r(A)+r(A-E)≤n,于是A的线性无关的
特征向量的总个数为
n-r(0·E-A)+n-r(1·E-A)=2n-[r(-A)+r(E-A)]≥2n-n=n,
故A有n个线性无关的特征向量,则A可相似对角化.
同理,B的特征值为0或1,可相似对角化,且由题设,r(A)=r(B),可知A、B有完全相同的特征值,即A、B相似于同一对角阵.故A、B必相似.
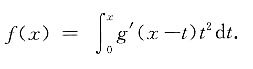 则
则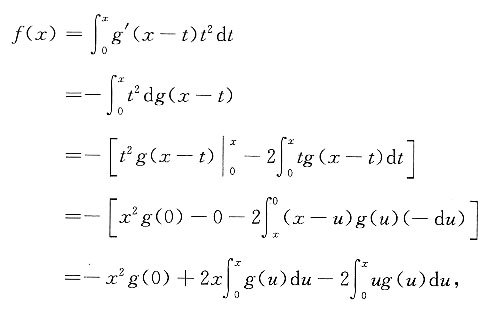

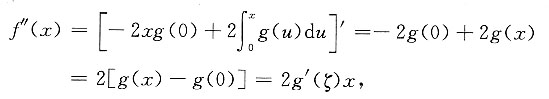
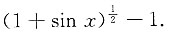
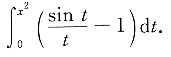
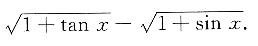

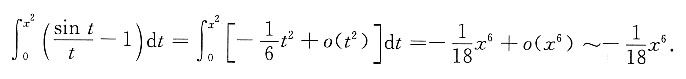
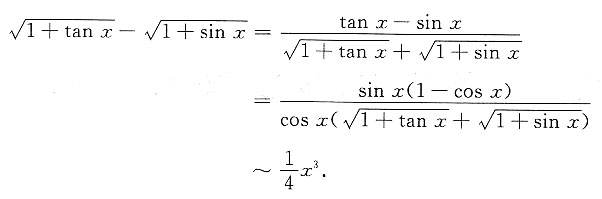
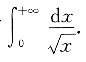
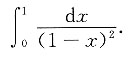
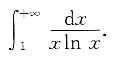
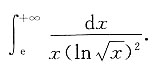

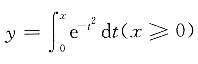 和其水平渐近线
和其水平渐近线 以及y轴所围区域的面积A为
以及y轴所围区域的面积A为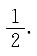
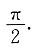
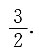
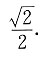
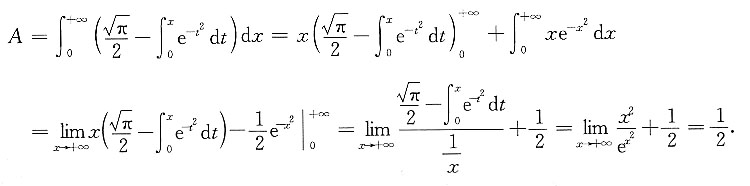
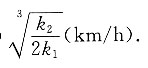
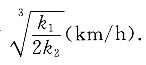

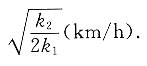
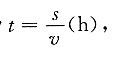 所以有
所以有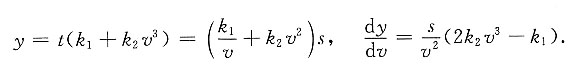
 时,
时,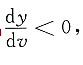 y单调递减;
y单调递减;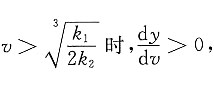 y单调递增.
y单调递增.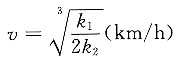 时,航行总费用最省.
时,航行总费用最省.
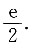
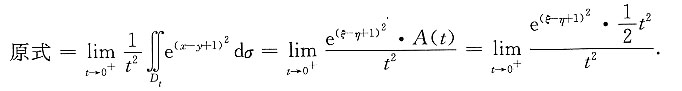

 k为任意常数,则以下5个向量组,
k为任意常数,则以下5个向量组,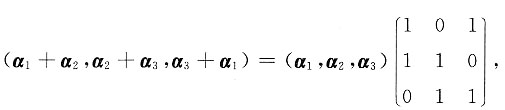
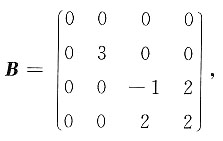 矩阵A~B,则秩r(A-E)+r(A-3E)=
矩阵A~B,则秩r(A-E)+r(A-3E)=
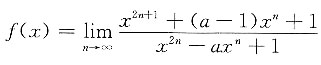 在区间(0,+∞)上连续的充要条件是a=______.
在区间(0,+∞)上连续的充要条件是a=______.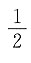
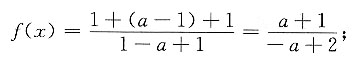
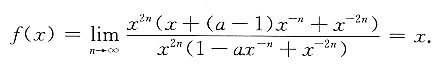
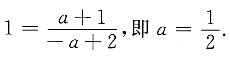 而在x>0的其它处,无论a取什么值,f(x)总是连续的.所以f(x)在(0,+∞)上连续的充要条件是
而在x>0的其它处,无论a取什么值,f(x)总是连续的.所以f(x)在(0,+∞)上连续的充要条件是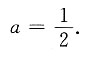
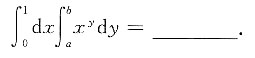
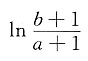
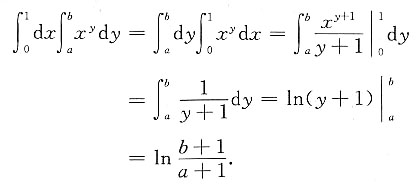
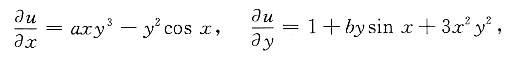
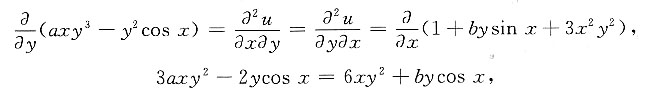
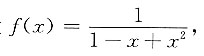 则f(2 016)(0)=______.
则f(2 016)(0)=______.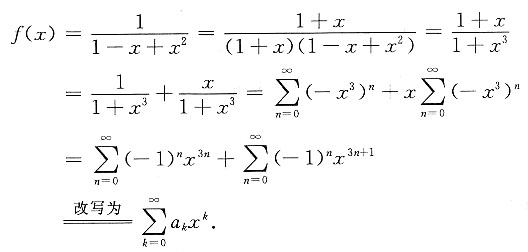
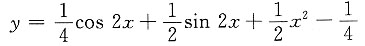
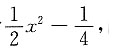 因而非齐次方程的通解为
因而非齐次方程的通解为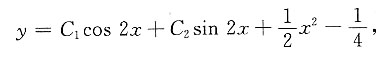
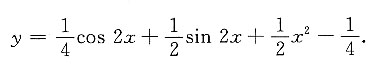
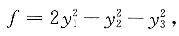 A*是A的伴随矩阵,且向量α=(1,1,-1)T满足A*α=α,则二次型f(x1,x2,x3)=______.
A*是A的伴随矩阵,且向量α=(1,1,-1)T满足A*α=α,则二次型f(x1,x2,x3)=______.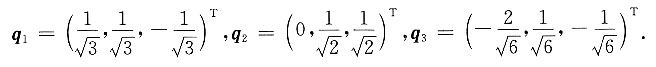
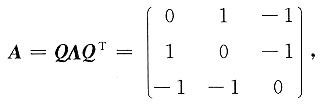

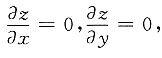 联立方程得
联立方程得
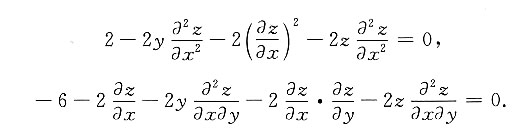
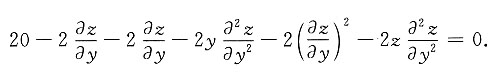
 点(12,4,4)1代入得
点(12,4,4)1代入得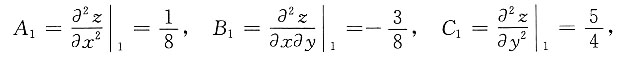
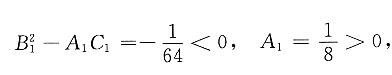
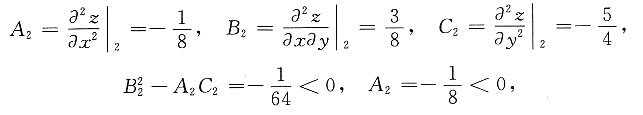
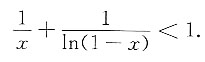
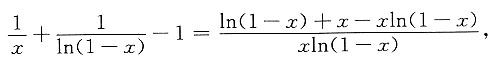
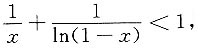 等价于证明,当x<1且x≠0时
等价于证明,当x<1且x≠0时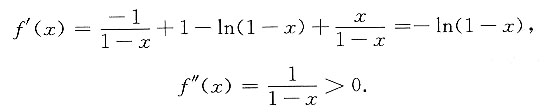
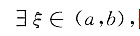 使得
使得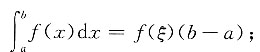
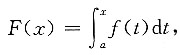 则F(x)在[a,b]上满足拉格朗日中值定理的条件.
则F(x)在[a,b]上满足拉格朗日中值定理的条件.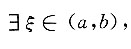 使得
使得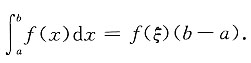
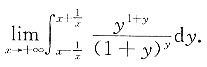
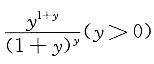 是连续的,由积分中值定理,存在
是连续的,由积分中值定理,存在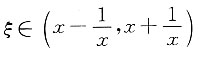 (x>0),使
(x>0),使
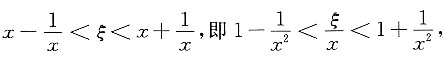 而在x→+∞时,有
而在x→+∞时,有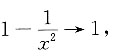
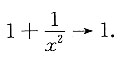 由夹逼定理可知,x→+∞时,
由夹逼定理可知,x→+∞时,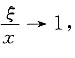 且有ξ→+∞,故
且有ξ→+∞,故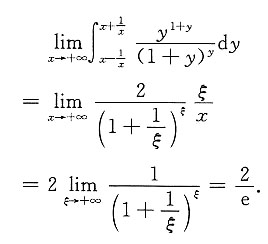
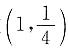 点与直线4x-4y-3=0相切,且y=y(x)满足方程
点与直线4x-4y-3=0相切,且y=y(x)满足方程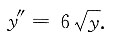 求该曲线在相应x∈[-1,1]上点(x,y)处的曲率.
求该曲线在相应x∈[-1,1]上点(x,y)处的曲率.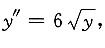 得
得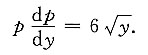
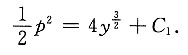
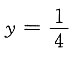 时,p=1,得C1=0.从而
时,p=1,得C1=0.从而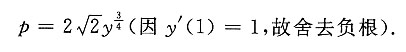

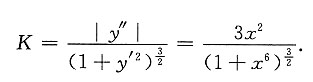
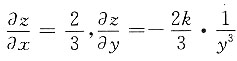 (k是正常数),且
(k是正常数),且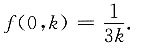
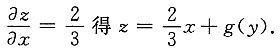 而
而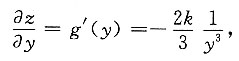
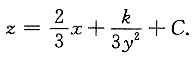 再由
再由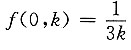 得C=0,所以
得C=0,所以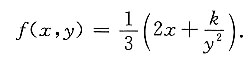
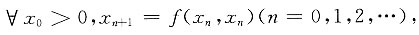 证明:数列{xn}收敛,并求
证明:数列{xn}收敛,并求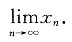
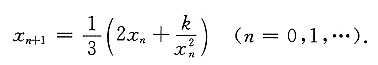
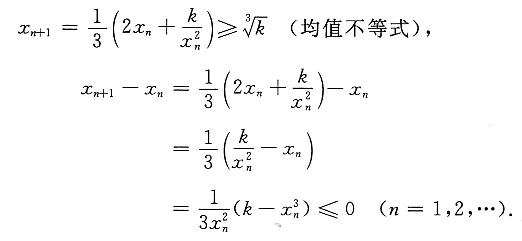
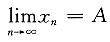 得
得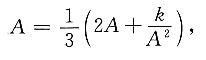
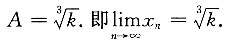
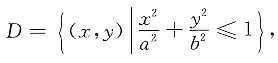 其中常数a>0,b>0,求二重积分
其中常数a>0,b>0,求二重积分