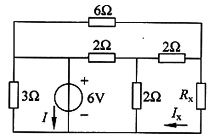
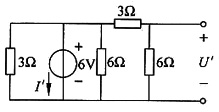
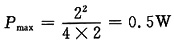解答题1. 已知下图所示电路中电流I
x=0.5A。求电阻R
x及电流I。
解 解法1:将题干图中3个2Ω电阻做
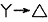
变换,所得电路如下图(a)所示。
图(a)
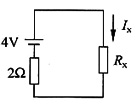
图(a)所示电路的戴维南等效电路如图(b)所示。
图(b)
由图(b)有
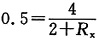
,解得R
x=6Ω。
由图(a)电路求得
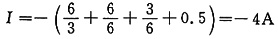
解法2:对图(a)电路应用替代定理再进行叠加,所得电路如图(c)、(d)所示。
图(c)
图(d)
图(c)所示电路中
U'=4V,
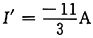
图(d)所示电路中
U"=-1V,
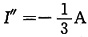
由叠加定理得
U=U'+U"=-1+4=3V,I=I'+I"=-4A
再由图(a)所示电路得
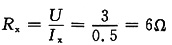
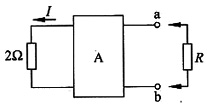
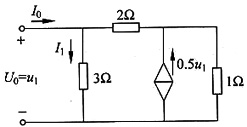
2. 求a,b两端戴维南等效电路
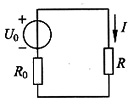
解 a,b两端戴维南等效电路如下图(a)所示。
图(a)
由图(a)和已知条件有
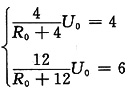
解得U
0=8V,R
0=4Ω。
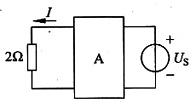
3. a,b两端接入电阻R为何值时,2Ω电阻中电流I=1.9A
解 设R两端电压为U
S,利用替代定理,原电路等效为图(b)所示。
图(b)
设U
S单独作用,在2Ω电阻产生电流为GU
S;框内电源单独作用,在2Ω电阻产生电流为I'。由叠加定理得
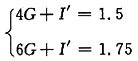
解得G=0.125S,I'=1A。
在2Ω电阻中产生1.9A电流所需电压由GU
S+I'=1.9求得,为U
S=7.2V。再由图(a)有
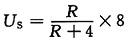
解得R=36Ω。
4. 求下图所示电路中负载电阻R
L上的电压U
L。
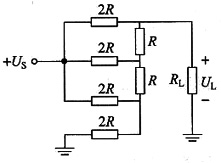
解 用戴维南定理求解。
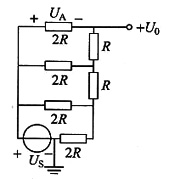
求开路电压U
0的电路如下图(a)所示,可得关系式
U
0=-U
A+U
S 图(a)
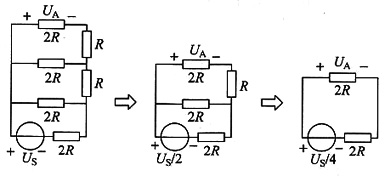
U
A可根据图(a)电路由下往上逐级电源等效变换求得(如图(b)所示),则
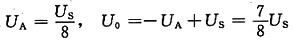
图(b)
由图(a)电路求得内阻R
i=R。
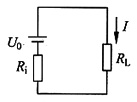
戴维南等效电路如图(c)所示,由此得
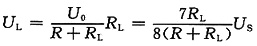
图(c)
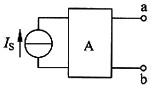
5. 图1所示电路中,方框内部为一含有独立电源的电阻网络A。已知
(1)当I
S=1A时,a,b间开路电压U
ab=5V;
(2)当I
S=2A时,a,b间开路电压U
ab=7V;
(3)当I
S=0时,a,b间短路电流I
ab=1A。
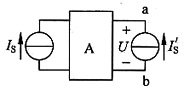
现在a,b间另接一电流源I'
S(图2(a)所示电路)。求当I
S=-3A,I'
S=4A时的电压U。
图1
图2(a)
解 对图1电路应用叠加定理,得图2(b)所示电路。其中,U'
ab为I
S=1A单独作用产生的电压,U"
ab为A中电源单独作用产生的电压。
图2(b)
根据已知条件(1),(2)有
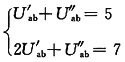
解得U'
ab=2V,U"
ab=3V。
由已知条件(3)有
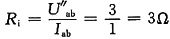
对图2(a)电路应用叠加定理,得图2(c)所示电路。
图2(c)
图2(c)所示电路中
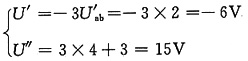
则
U=U'+U"=-6+15=9V
图(a)
图(b)
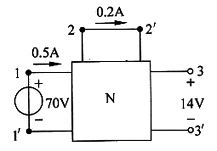
6. R=210Ω时,电流i
1
解 由特勒根定理得
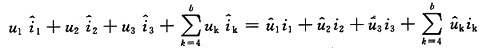
(1)
因为
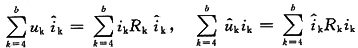
则式(1)变为
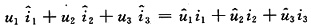
(2)
将题目所给条件:
u
1=70V,u
2=0,u
3=14V,i
1=-0.5A,i
2=0.2A,i
3=0 (对应图(a));
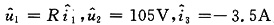
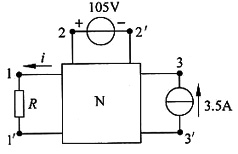
,且
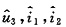
均未知 (对应图(b))。
代入式(2),得
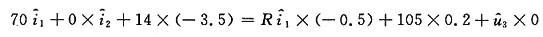
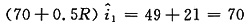
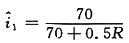
(3)
当R=210Ω时,
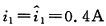
。
7. R为何值时,其上获得最大功率,并求此最大功率
解 由图(a)可求出图(b)11'右边电路戴维南等效电路中等效内阻R
i=70/0.5=140Ω,所以R=140Ω时功率最大,此时(利用式(3))
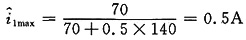
P
max=0.5
2×140=35W
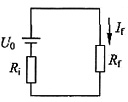
8. 下图所示电路中,方框部分为含独立源和电阻的网络。当端口a,b短接时,电阻R支路中电流I=I
S1。当端口a,b开路时,电阻R支路中电流I=I
S2。当端口a,b间接电阻R
f时,R
f获得最大功率。求端口a,b间接电阻R
f时,流过R支路的电流I。
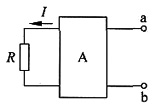
解 题干图的戴维南等效电路如下图(a)所示。
图(a)
设流过R
f的电流为I
f,当R
f=R
i时R
f获最大功率
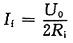
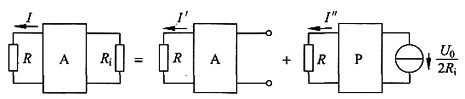
根据叠加定理和替代定理,将待求电路分为2个电路,如图(b)所示。
图(b)
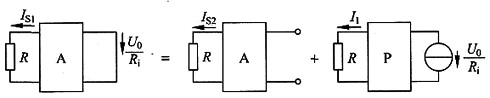
根据已知条件并应用叠加定理和替代定理得电路如图(c)所示。
图(c)
比较图(b)和图(c),可得
I'=I
S2,
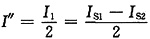
所以
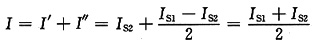
9. 求下图所示电路中的电流I(运算放大器为理想运算放大器)。
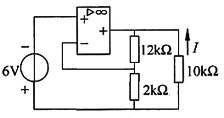
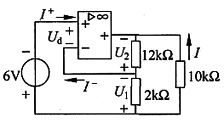
解 分析运算放大器电路的关键,是运算放大器电路两输入端的虚短路和虚开路特性。由下图所示的运算放大器两输入端的虚短路和虚开路特性,可得
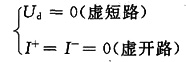
U
1=6V
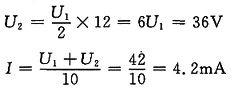
10. 已知u
S(t)=5cosωtV,求电流i(运算放大器为理想运算放大器)。
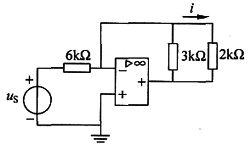
解 重画电路如下图所示,A点电位为零,则
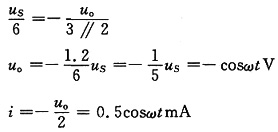

11. 电路如下图所示。试分别求12V电压源和5A电流源发出的功率。
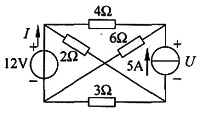
解 只需求出U和I,即可求出两个电源发出的功率。可采用叠加的方法。
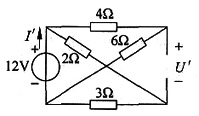
电压源单独作用时(见图(a)),有
图(a)
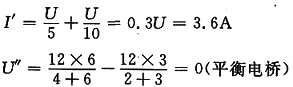
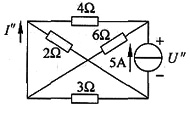
电流源单独作用时(见图(b)),有
图(b)
U"=5×(4∥6+2∥3)=18V
I"=0(平衡电桥)
则
P
12V发=12I=12×3.6=43.2W
P
5A发=5U=5×18=90W
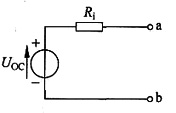
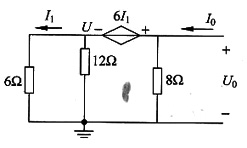
12. 求下图所示电路的戴维南等效电路。
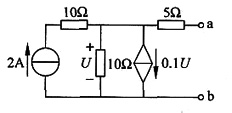
解 戴维南等效电路如图(a)所示。
图(a)
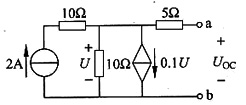
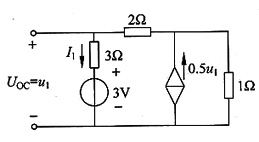
(1)求开路电压(见图(b))
图(b)
U
OC=U=10×(2-0.1U)
U=10V=U
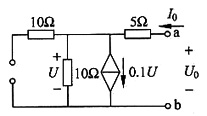
(2)求等效电阻(将电流源开路见图(c))
图(c)
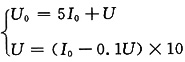
得
U
0=5I
0+5I
0=10I
0 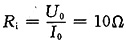
13. 求下图所示电路中R为何值时能获得最大功率,并求此最大功率。
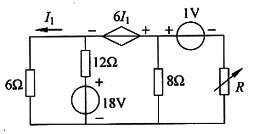
求戴维南等效电路,求开路电压(见图(a))
图(a)
U
OC=1+6I
1+6I
1=-1+12I
1 列节点方程
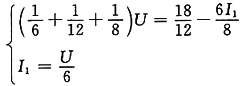
解得
U=3V,
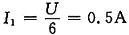
U
OC=-1+12I
1=-1+6=5V
(2)求等效电阻(见图(b))
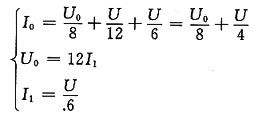
图(b)
解得
U
0=12I
1=2U,U=0.5U
0 则
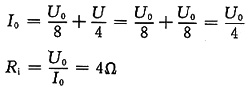
当R=R
i=4Ω时,其上获最大功率
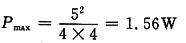
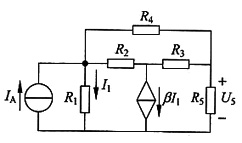
14. 电路如下图所示。已知I
S=1A,R
1=10Ω,R
2=R
3=R
4=30Ω,R
5=8Ω,β=9。求电压U
5。
解 经
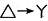
变换,原图可变换为图(a)所示电路,其中R
a=R
b=R
c=10Ω。
图(b)
解法1:节点法列方程
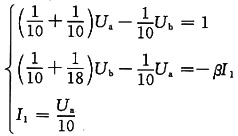
解上述方程,得U
b=-7.2V,
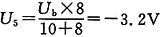
。
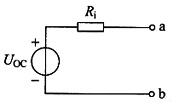
解法2:求ab以左电路的戴维南等效电路如图(b)所示,求开路电压
图(b)
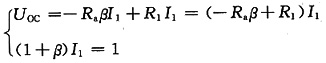
解得
U
OC=-8V
求等效电阻
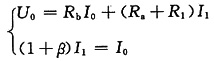
解得

则
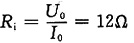
可得
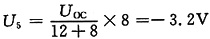
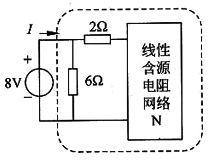
15. 下图(a)电路中电流I=2A,图(b)电路中电压U=6V,求图(c)电路中电流I。
图(a)
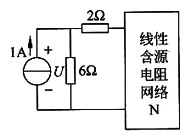
图(b)
图(c)
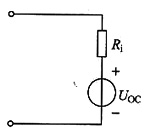
解 解法1:求线性含源电阻网络N的戴维南等效电路(图(d)所示电路)
图(d)
由图(a)所示电路,得
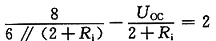
由图(b)所示电路,得
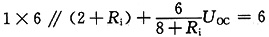
解得U
OC=6V,R
i=1Ω。
由图(c)所示电路,解得
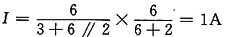
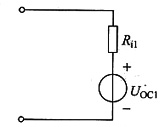
解法2:求虚线框内电路的戴维南等效电路(图(e)所示电路)
图(e)
由图(a)所示电路,得
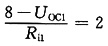
由图(b)所示电路,得
1×R
i1+U
OC1=6
解得U
OC1=4V,R
i1=2Ω。
由图(c)所示电路,解得
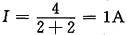
16. 电路如下图所示。当R的值为多大时可获得最大功率?并求该最大功率。
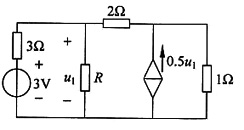
解 题干图电路的戴维南等效电路如下图(a)所示。求开路电压(见图(b))
图(a)
图(b)
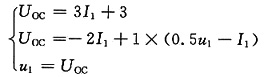
解得U
OC=2V。
求等效电阻(见图(c))
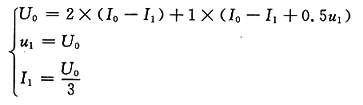
图(c)
解得
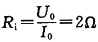
,则R=R
i=2Ω时,其上获最大功率
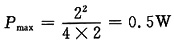

 变换,所得电路如下图(a)所示。
变换,所得电路如下图(a)所示。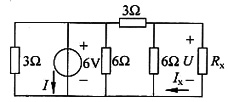
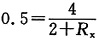 ,解得Rx=6Ω。
,解得Rx=6Ω。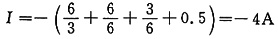

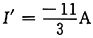
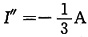
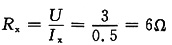

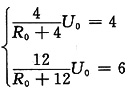
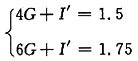
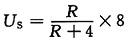

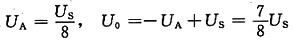
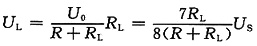
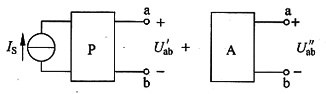
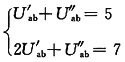
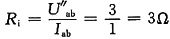

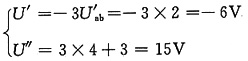
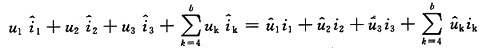 (1)
(1)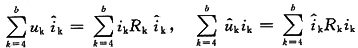
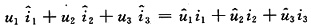 (2)
(2)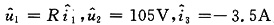 ,且
,且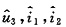 均未知 (对应图(b))。
均未知 (对应图(b))。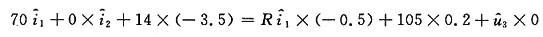
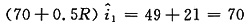
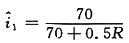 (3)
(3)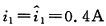 。
。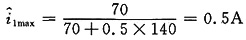

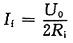
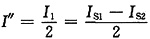
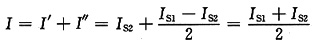

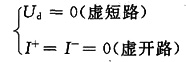
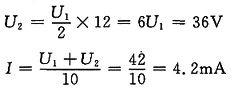


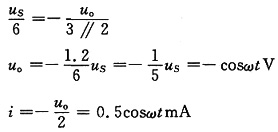


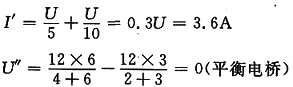

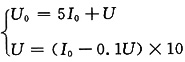
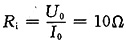


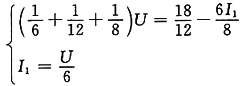
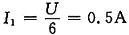
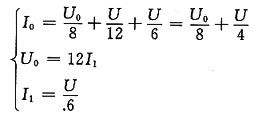
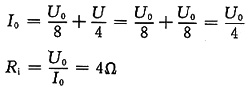
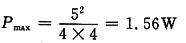

 变换,原图可变换为图(a)所示电路,其中Ra=Rb=Rc=10Ω。
变换,原图可变换为图(a)所示电路,其中Ra=Rb=Rc=10Ω。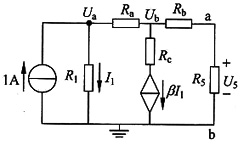
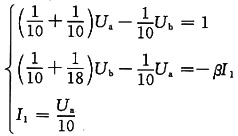
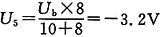 。
。
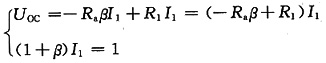
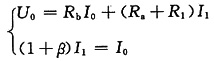

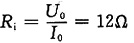
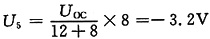

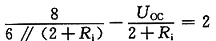
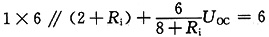
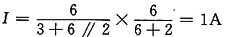
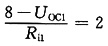
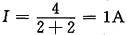


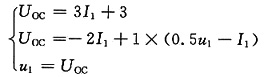
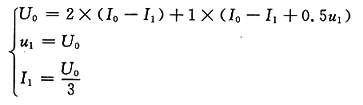
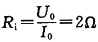 ,则R=Ri=2Ω时,其上获最大功率
,则R=Ri=2Ω时,其上获最大功率