第一部分 选择题
一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的
3. 设λ
1与λ
2是矩阵A的两个不同的特征值,ε,η是A的分别属于λ
1,λ
2的特征向量,则______
- A.存在常数k1≠0,k2≠0,使k1ε+k2η是A的特征向量
- B.存在唯一的一组常数k1≠0,k2≠0,k1ε+k2η是A的特征向量
- C.对任意k1≠0,k2≠0,k1ε+k2η是A的特征向量
- D.当k1≠0,k2≠0时,k1ε+k2η不可能是A的特征向量
A B C D
D
[考点] 特征向量
[解析] 假设k
1ε+k
2η是A的属于λ的特征向量,
即A(k
1ε+k
2η)=λ(k
1ε+k
2η),
即(k
1λ
1ε+k
2λ
2η)=λk
1ε+λk
2η,
即(k
1λ
1-k
1λ)ε+(k
2λ
2-k
2λ)η=0,
而ε与η分属于A的两个不同特征值的特征向量,
故线性无关,故
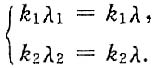
又k
1,k
2都不为0,得λ=λ
1=λ
2与λ
1≠λ
2矛盾.
故当k
1≠0,k
2≠0时,k
1ε+k
2η不可能是A的特征向量,选D.
4. 设三元实二次型
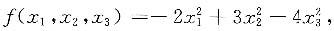
则其规范形为______
A.
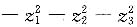
B.
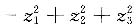
C.
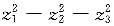
D.
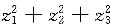
A B C D
C
[考点] 求二次型的规范型
[解析] 三元二次型
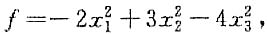
经过可逆线性变换:
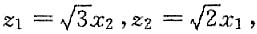
z
3=2x
3,则其规范型为
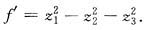
5. 设λ
0是n阶矩阵A的特征值,且齐次线性方程组(λ
0E-A)x=0的基础解系为η
1和η
2,则A的属于λ
0的全部特征向量是______
- A.η1和η2
- B.C1η1+C2η2+C2(C1,C2为任意常数)
- C.C1η1+C2η2(C1,C2为不全为零的任意常数)
- D.η1或η2
A B C D
C
[考点] 特征向量
[解析] 对任意常数C
1,C
2,都有(λ
0E-A)(C
1η
1+C
2η
2)=C
1(λ
0E-A)η
1+C
2(λ
0E-A)η
2=0.
即有
A(C
1η
1+C
2η
2)=λ
0(C
1η
1+C
2η
2).
但又由于零向量不是特征向量.
故属于λ
0的全部特征向量即为C
1η
1+C
2η
2,(
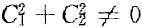
),故选C.
第二部分 非选择题
二、填空题1. 行列式

的值为______.
0
[考点] 行列式计算
[解析]
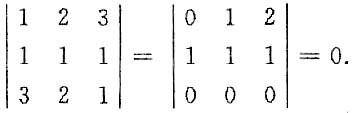
2. 设A是n阶方阵,A
*为A的伴随矩阵,|A|=5,则方阵B=AA
*的特征值是______,特征向量是______.
5 任意n维非零向量α
[考点] 特征值与特征向量
[解析] 因为AA*=A*A=|A|E,所以对于任意n维非零向量α,有AA*α=|A|Eα=|A|α.所以|A|=5是B=AA*的特征值,任意n维非零向量α为其对应的特征向量.
3. 已知矩阵
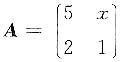
有一个特征值为0,则x=______.
[考点] 特征值的性质
[解析] A的行列式等于A的所有特征值的乘积,因为A有一个特征值为0,所|A|=5-2x=0,
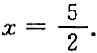
4. 三阶方阵A的特征值为1,-1,2,则B=2A
3-3A
2的特征值为______.
-1,-5,4
[考点] 特征值的求法
[解析] 设A的特征向量α,对应特征值λ,则有
Bα=(2A3-3A2)α=2A3α-3A2α=2λ3α-3λ2α=(2λ3-3λ2)α,故2λ3-3λ2是B的特征值.
5. 已知矩阵A与对角矩阵

相似,则A
2=______.
E
[考点] 相似矩阵
[解析] 因A与D相似,且

则存在可逆矩阵T,使得TAT
-1=D.
则
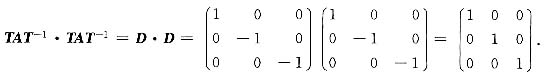
即

两边分别左乘T
-1,右乘T,
则
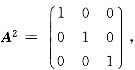
即A
2=E.
6. 设
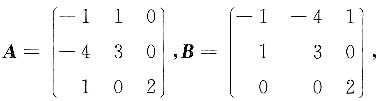
且A的特征值为2和1(二重),那么B的特征值为______.
2和1(二重)
[考点] 特征值的求法
[解析] 因为|λE-A|=|(λE-A)T|=|λE-AT|,即A与AT有相同的特征多项式,故有相同的特征值,又AT=B.故B的特征值即为2和1(二重).
7. 设二次型
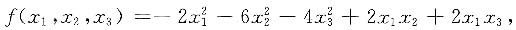
则二次型对应的矩阵为______.
[考点] 二次型及其标准形
[解析] 由对称性易知为
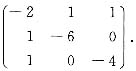
8. 已知矩阵
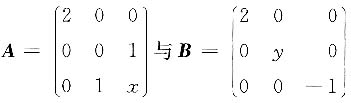
相似,则x=______,y=______.
0,1
[考点] 实对称矩阵的相似
[解析] 因A~B,故tr(A)=tr(B),故2+x=2+y-1.
又因A~B,故|A|=|B|,故-2=-2y,故y=1,x=0.
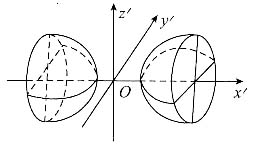
9. 设A为3阶实对称矩阵,如果二次曲面方程

在正交变换下的标准方程的图形如图所示,则A的正特征值的个数为______.
1
[考点] 空间解析几何与线性代数的问题
[解析]
由图形可知二次曲面为双叶双曲面,其标准方程应为

从而方程左端对应二次型的正惯性指数为1,即正特征值的个数为1.
10. 设A,B为n阶方阵,且|A|≠0,则仙和BA相似,这是因为存在可逆矩阵P=______,使得P
-1ABP=BA.
A
[考点] 相似矩阵
[解析] 由|A|≠0知A可逆,又A-1(AB)A=BA,故P=A.
三、计算题本大题共7小题,每小题9分,共63分
1. 设A为n阶实对称矩阵,且A
3-3A
2+5A-3E=0.证明:A正定.
证明:设λ是A的任一特征值,对应特征向量为x≠0,即Ax=λx,则有
(A
3-3A
2+5A-3E)x=(λ
3-3λ
2+5λ-3)x=0,
也即λ满足 λ
3-3λ
2+5λ-3=(λ-1)(λ
2-2λ+3)=0,
解得λ=1或
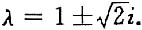
因为A为实对称矩阵,其特征值为实数,故只有λ=1,即A的全部特征值就是λ=1>0,所以A为正定矩阵.
[考点] 正定矩阵
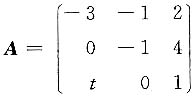 的特征值,求:
的特征值,求:2. t的值;

即t为任何值时,矩阵都有特征值1.
3. 对于λ=1的所有特征向量.
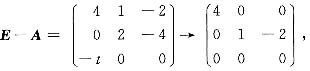
取x
3为自由未知量,并令x
3=1,得ε=(0,2,1)
T.
即属于λ=1的全部特征向量为kε=k(0,2,1)
T,k任取但不为0.
[考点] 特征值与特征向量
4. 设A为m×n实矩阵,E为n阶单位矩阵,已知矩阵B=λE+A
TA,试证:当λ>0时,矩阵B为正定矩阵.
证明:因为B
T=(λE+A
TA)
T=λE+A
TA=B,所以B是n阶实对称矩阵,构造二次型x
TBx,那么
x
TBx=x
T(λE+A
TA)x=λx
Tx+x
TA
TAx=λx
Tx+(Ax)
T(Ax).
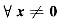
,恒有x
Tx>0,(Ax)
T(Ax)≥0,因此,λ>0时,
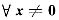
,有x
TBx=λx
Tx+(Ax)
T(Ax)>0.
二次型为正定型,故B为正定矩阵.
[考点] 正定矩阵
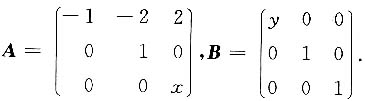
5. 求x和y的值;
A的特征值为-1,1,x;B的特征值为y,1,1.
A~B,故特征值相同,相比较得y=-1,x=1.
6. 求可逆矩阵P,使得P
-1AP=B.
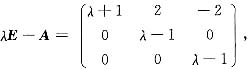
令λ=1,解(λE-A)x=0得ε
1=(1,1,0)
T,ε
2=(1,0,1)
T.
再令λ=-1,解(λE-A)x=0得ε
3=(1,0,0)
T.
取
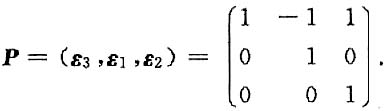
则有P
-1AP=B.
[考点] 实对称矩阵的相似
7. 设有n元实二次型f(x
1,x
2,…,x
n)=(x
1+a
1x
2)
2+(x
2+a
2x
3)
2+…+(x
n-1+a
n-1x
n)
2+(x
n+a
nx
1)
2,其中a
i(i=1,2,…,n)为实数,试问:当a
1,a
2,…,a
n满足何种条件时,二次型f(x
1,x
2,…,x
n)为正定二次型?
由已知条件知,对任意的x
1,x
2,…,x
n,恒有f(x
1,x
2,…,x
n)≥0,
其中等号成立的充分必要条件是
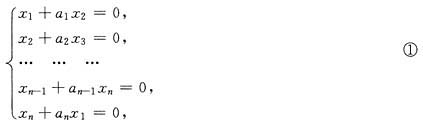
根据正定的定义,只要x≠0,恒有x
TAx>0,则x
TAx是正定二次型,为此,只要方程组(1)仅有零解,就必有当x≠0时,x
1+a
1x
2,x
2+a
2x
3,…不全为0,从而f(x
1,x
2,…,x
n)>0,亦即f是正定二次型.而方程组①中只有零解的充分必要条件是系数行列式
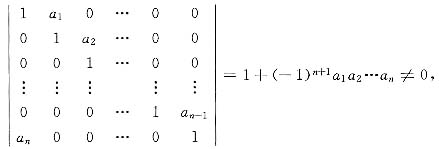
即当a
1a
2…a
n≠(-1)
n时,二次型f(x
1,x
2,…,x
n)为正定二次型.
[考点] 正定二次型
8. 设

求A
100.
可求得A的特征值λ
1=-1,λ
2=1,λ
3=2,对应特征向量分别为
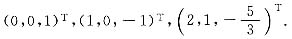
令
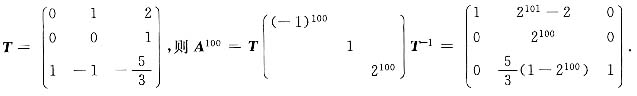
[考点] 相似矩阵

9. 记x=(x
1,x
2,…,x
n)
T,把f(x
1,x
2,…,x
n)写成矩阵形式,并说明二次型f(x)的矩阵为A
-1;
由于
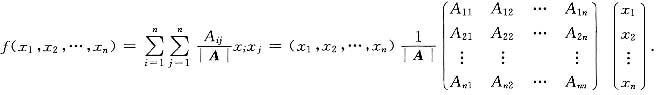
因为r(A)=n,知A可逆,又因A是实对称的,有(A
-1)
T=(A
T)
-1=A
-1,
可知
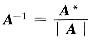
是实对称矩阵,于是A
*是对称的,故二次型f(x)的矩阵是A
-1.
10. 二次型g(x)=x
TAx与f(x)的规范形是否相同?说明理由.
经坐标变换x=A-1y,有
g(x)=xTAx=(A-1y)TA(A-1y)=yT(A-1)Ty=yTA-1y=f(y).
即g(x)与f(x)有相同的规范形.
[考点] 实二次型
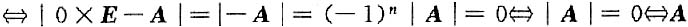 不可逆.故选D.
不可逆.故选D.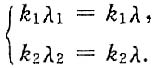
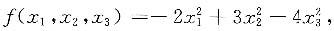 则其规范形为______
则其规范形为______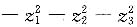
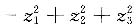
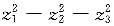
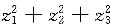
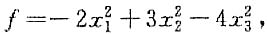 经过可逆线性变换:
经过可逆线性变换: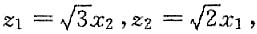 z3=2x3,则其规范型为
z3=2x3,则其规范型为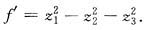
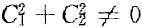 ),故选C.
),故选C. 的值为______.
的值为______.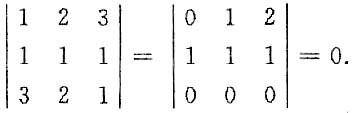
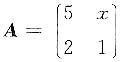 有一个特征值为0,则x=______.
有一个特征值为0,则x=______.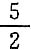
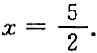
 相似,则A2=______.
相似,则A2=______. 则存在可逆矩阵T,使得TAT-1=D.
则存在可逆矩阵T,使得TAT-1=D.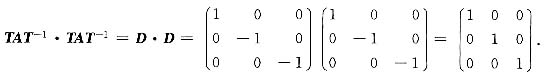
 两边分别左乘T-1,右乘T,
两边分别左乘T-1,右乘T,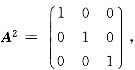
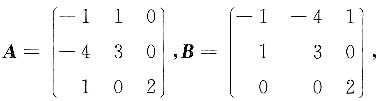 且A的特征值为2和1(二重),那么B的特征值为______.
且A的特征值为2和1(二重),那么B的特征值为______.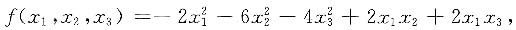 则二次型对应的矩阵为______.
则二次型对应的矩阵为______.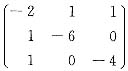
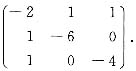
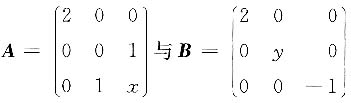 相似,则x=______,y=______.
相似,则x=______,y=______. 在正交变换下的标准方程的图形如图所示,则A的正特征值的个数为______.
在正交变换下的标准方程的图形如图所示,则A的正特征值的个数为______.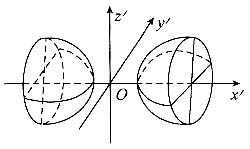

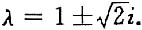
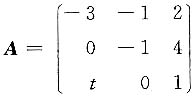 的特征值,求:
的特征值,求: 即t为任何值时,矩阵都有特征值1.
即t为任何值时,矩阵都有特征值1.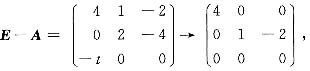
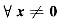 ,恒有xTx>0,(Ax)T(Ax)≥0,因此,λ>0时,
,恒有xTx>0,(Ax)T(Ax)≥0,因此,λ>0时,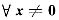 ,有xTBx=λxTx+(Ax)T(Ax)>0.
,有xTBx=λxTx+(Ax)T(Ax)>0.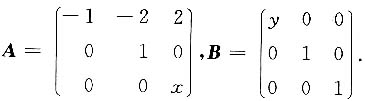
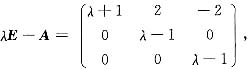
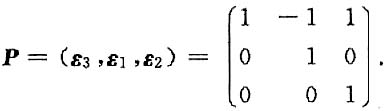
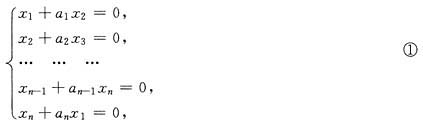
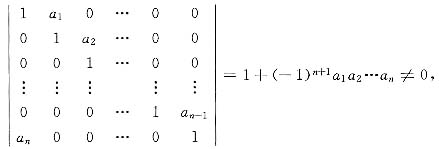
 求A100.
求A100.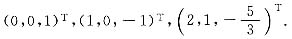
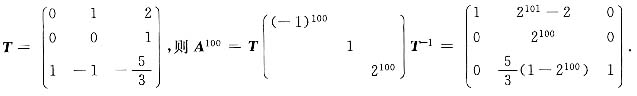

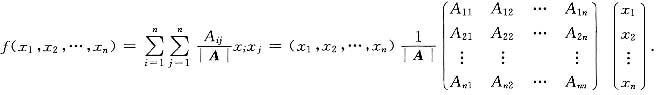
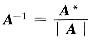 是实对称矩阵,于是A*是对称的,故二次型f(x)的矩阵是A-1.
是实对称矩阵,于是A*是对称的,故二次型f(x)的矩阵是A-1.