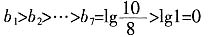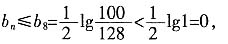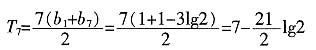一、填空题1. 设函数
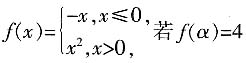
,则实数α=______。
2. 已知数列{a
n}的前n项和S
n满足:S
n+S
m=S
n+m,且a
1=1,那么a
10=______。
3. 若函数f(x)=x
2-|x+a|为偶函数,则实数a=______。
4. 设二项式
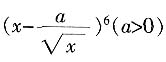
的展开式中x
3的系数为A,常数项为B,若B=4A,则a的值是______。
2
[解析] A=15a2,B=15a4,可得a=2。
5. 某班有36名同学参加数学、物理、化学课外探究小组,每名同学至多参加两个小组,已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参加数学和化学小组的有______人。
6. 若
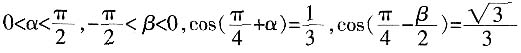
,则
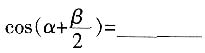
。
[解析]
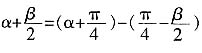
,然后根据两角差的余弦公式计算。
7. 若a,b为实数,则“0<ab<1”是
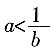
或
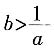
的______条件。
充分而不必要
[解析] 由0<ab<1得到
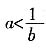
或
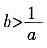
,反之则不一定。
8. 如图:AB=10cm是半圆的直径,C是AB弧的中点,ABD是以AB为半径的扇形,则图中阴影部分的面积是______。
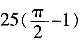
平方厘米
[解析] 连结AC可知,阴影面积=扇形ABD面积-△ACB面积
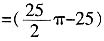
平方厘米。
9. 设单位向量m=(x,y),b=(2,-1)。若m⊥b,则|x+2y|=______。
[解析] 由已知可得2x-y=0,又因为m为单位向量所以x
2+y
2=1,联立解得

或
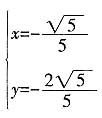
代入所求即可。
10. 设x,y为实数,若4x
2+y
2+xy=1,则2x+y的最大值是______。
[解析] 设2x+y=m,与已知方程联立,根据Δ≥0求得m的最大值。
二、选择题在每小题4个备选答案中。选出一个符合题意的正确答案。2. 设函数
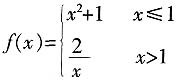
,则f(f(3))=
A.
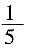
B.3
C.
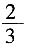
D.
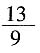
A B C D
D
[解析] 考查分段函数
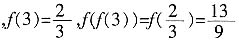
。
3. 若

,则tan2α=
A.
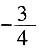
B.
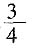
C.

D.

A B C D
B
[解析] 主要考查三角函数的运算,分子分母同时除以cosα可得tanα=-3,带入所求式可得结果。
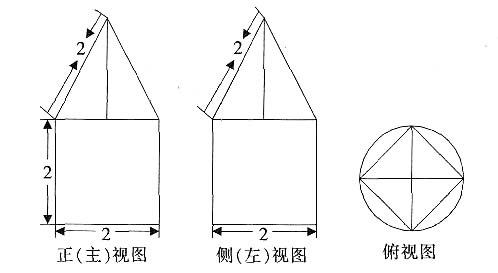
4. 一空间几何体的三视图如图所示,则该几何体的体积为
A.
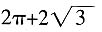
B.
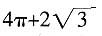
C.
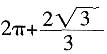
D.
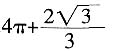
A B C D
C
[解析] 该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为2π,四棱锥的底面边长为
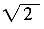
,高为
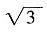
,所以体积为
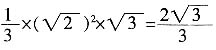
,则该几何体的体积为
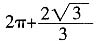
。
6. 函数
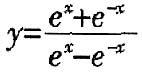
的图像大致为
A.
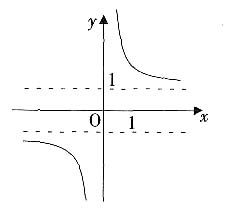
B.
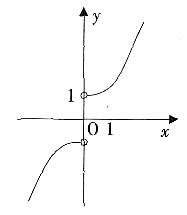
C.
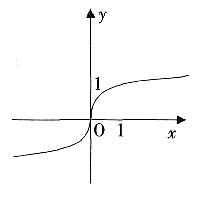
D.
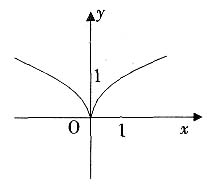
A B C D
A
[解析] 函数有意义,需使e
x-e
-x≠0,其定义域为{x|x≠0},排除C、D;又因为
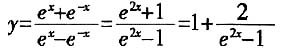
,所以当x>0时函数为减函数,故选A。
9. 设双曲线
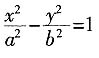
的一条渐近线与抛物线y=x
2+1只有一个公共点,则双曲线的离心率为
A.
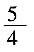
B.5
C.
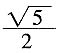
D.
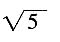
A B C D
D
[解析] 双曲线
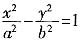
的一条渐近线为
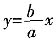
,由方程组

消去y,得
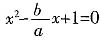
,有唯一解,所以Δ=0,得
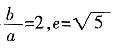
。
三、解答题设函数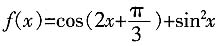 。
。1. 求函数f(x)的最大值和最小正周期。
解:
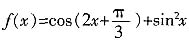
,化简为
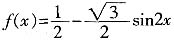
,所以函数f(x)的最大值为
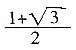
,最小正周期π。
2. 设A、B、C为△ABC的三个内角,若
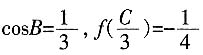
,且C为锐角,求sinA。
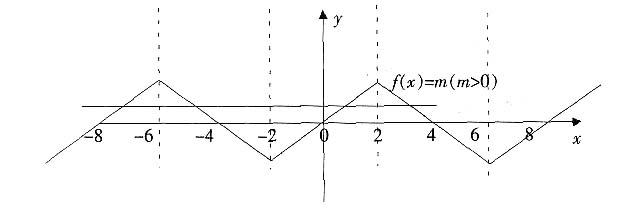
3. 已知定义在R上的奇函数f(x),满足f(x-4)=f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x
1、x
2、x
3、x
4,求四数之和x
1+x
2+x
3+x
4。
解:因为定义在R上的奇函数,满足f(x-4)=-f(x),所以f(x-4)=f(-x)。由f(x)为奇函数,所以函数图象关于直线x=2对称且f(0)=0。
由f(x-4)=-f(x)知f(x-8)=f(x),所以函数是以8为周期的周期函数。又因为f(x)在区间[0,2]上是增函数,所以f(x)在区间[-2,0]上也是增函数。
如图所示,那么方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x
1,x
2,x
3,x
4,不妨设x
1<x
2<x
3<x
4,由对称性知x
1+x
2=-12、x
3+x
4=4。所以x
1+x
2+x
3+x
4=-12+4=-8。
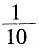 和p。
和p。4. 若在任意时刻至少有一个系统不发生故障的概率为
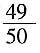
,求p的值;
解:设“至少有一个系统不发生故障”为事件C,那么
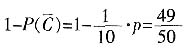
解得
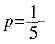
5. 设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ。
解:由题意,
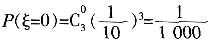
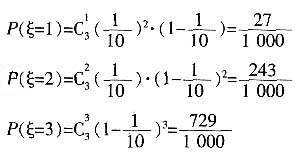
所以,随机变量ξ的概率分布为

故随机变量ξ的数学期望:
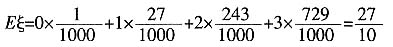
6. 求a
1,a
2的值;
解:取n=1,得a
2a
1=S
2+S
1=2a
1+a
2 ①
取n=2,得
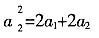
②
由②-①,得a
2(a
2-a
1)=a
2 ③
(Ⅰ)若a
2=0,由①知a
1=0
(Ⅱ)若n
2≠0,由③知a
2-a
1=1 ④
由①、④解得,
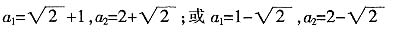
综上可得,a
1=0,a
2=0;或
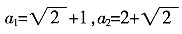
;或
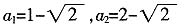
7. 设a
1>0,数列
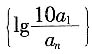
的前n项和为T
n,当n为何值时,T
n最大?并求出T
n的最大值。
解:当a
1>0时,由(1)知
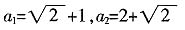
当n≥2时,有
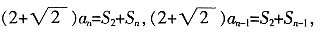
所以
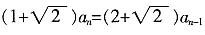
,即
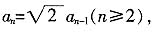
所以
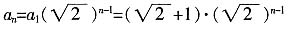
令
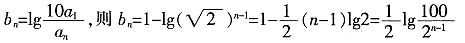
所以数列{b
n}是单调递减的等差数列
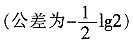
,从而
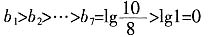
当n≥8时,
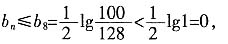
故n=7时,T
n取得最大值,且T
n的最大值为
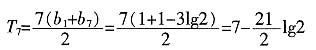
五、教学设计题1. 根据下面给出的题目,试编写出科学可行的教学片段。
教学片段:
师:课前老师让你们收集了带有百分数的物品,请拿出来。(学生拿出了有关物品放在桌上。)
师:猜一猜今天我们将学习什么内容?
生:百分数。
师:谁来说一说?会读吗?知道它们的意义吗?
生1:羊毛含量占这件毛衣的90%,有90%是羊毛。
生2:这瓶酒的酒精含量占这瓶酒的48%,不太辣。
生3:实际完成是计划的150%,超额完成了。
生4:我国人数占全世界的25%,我国人口比较多。
生5:我国耕地面积占世界耕地的5%,人多地少,要控制人口,保护耕地。
生6:……
(多名学生上台介绍。)
[评析:数学课程标准明确:指出人人学有价值的数学;人人都能获得必需的数学;不同的人在数学上得到不同的发展。联系学生实际,创设情境,利用课前调查与数学信息收集,使学生初步了解百分数,调动了学生学习的自主性和能动性。]
师:谁会说一说百分数的意义吗?
生:一个数占另一个数百分之几的数叫百分数。
师:老师也收集了一些资料,谁来帮老师开个信息发布会。
(多媒体出示。)
1.一次性筷子是日本人发明的。日本的森林覆盖率达65%,我国的森林覆盖率达14%,但日本不砍伐自己国土上的树木做一次性筷子,我国却是一次性筷子的出口大国。
学生各抒己见。
生1:65%表示日本的森林面积占国土面积的65%。
生2:14%表示中国的森林面积占国土面积的14%。
生3:我们要注意保护森林环境,不能过度砍伐树木。
2.麦当劳、肯德基等洋快餐登陆扬州,据统计去年,洋快餐的营业额是中式快餐营业额的180%。
生1:洋快餐的营业额是中式快餐营业额的180%。
生2:洋快餐的营业额比中式快餐营业额多80%。
生3:中式快餐要在经营上多动脑筋,提高服务质量。
[评析:密切联系学生的生活实际,创设有趣、现实的情境,并以别开生面的“新闻发布会”的形式,让学生去充分讨论、合作交流、不断探索,充分发挥了学生的主体地位,使学生感悟到数学源于生活,激发了学生的学习热情。]
师:做游戏.分组比赛看谁算得快?(出示:7%______13%、130%______100%、25/72______12/59、2/15______5/12)
生:不公平,百分数进行比较方便,因为它们的分母都是100。
师:谁会用百分数表示成语吗?什么叫百发百中?什么叫百里挑一?什么叫一分为二?
生:百发百中是100%,百里挑一是1%,一分为二是50%。
师:你有什么发现?能提出哪些问题?
(从生活中的实物上提取而出示下列数据:0% 80% 100% 120% 200% 17.5% 3/4 3/4吨13/100 13%)
生1:百分号前的数可为0。
生2:百分号前的数可为小数。
生3:百分号前的数可以大于100。
生4:百分数不能带单位名称,因为百分数是一个比。
生5:3/4吨与3/4意义不一样,13/100与13%意义不一样。
生6:百分数怎么读?百分数怎么写?百分数的意义是什么?
生7:你会把这些百分数按从大到小的顺序排列吗?
[评析:在尝试练习、深化练习、拓展练习中使学生把生活经验知识转化成数学语言知识,让学生在练习中进一步领悟出百分数的意义,在习题设计上体现了趣味性,通过学生喜欢的游戏比赛,使他们在愉快中明白百分数的特征。让学生提问题,摆正了学生是数学学习的主人,教师是数学学习的组织者、引导者、合作者之间的关系,让学生能主动去思考、去探索,学会提出问题、分析问题、解决问题,拓展学生的思维,提高学生的综合素质。]
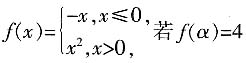 ,则实数α=______。
,则实数α=______。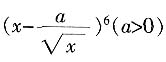 的展开式中x3的系数为A,常数项为B,若B=4A,则a的值是______。
的展开式中x3的系数为A,常数项为B,若B=4A,则a的值是______。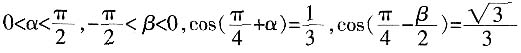 ,则
,则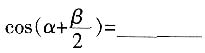 。
。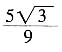
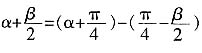 ,然后根据两角差的余弦公式计算。
,然后根据两角差的余弦公式计算。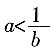 或
或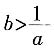 的______条件。
的______条件。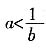 或
或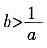 ,反之则不一定。
,反之则不一定。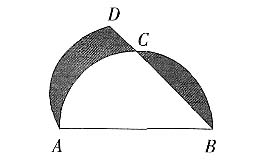
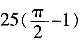 平方厘米
平方厘米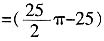 平方厘米。
平方厘米。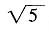
 或
或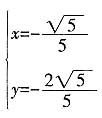 代入所求即可。
代入所求即可。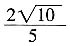
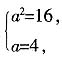 则a=4。
则a=4。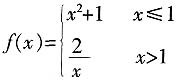 ,则f(f(3))=
,则f(f(3))=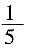
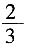
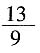
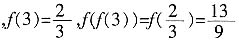 。
。 ,则tan2α=
,则tan2α=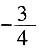
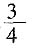


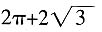
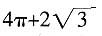
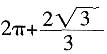
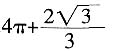
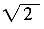 ,高为
,高为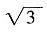 ,所以体积为
,所以体积为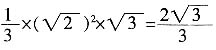 ,则该几何体的体积为
,则该几何体的体积为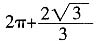 。
。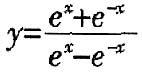 的图像大致为
的图像大致为



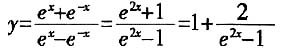 ,所以当x>0时函数为减函数,故选A。
,所以当x>0时函数为减函数,故选A。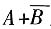 发生的概率为
发生的概率为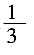
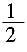
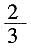
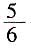
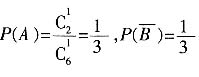 ,而与
,而与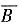 为互斥事件,故
为互斥事件,故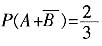 。
。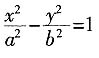 的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为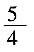
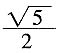
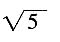
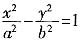 的一条渐近线为
的一条渐近线为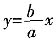 ,由方程组
,由方程组 消去y,得
消去y,得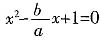 ,有唯一解,所以Δ=0,得
,有唯一解,所以Δ=0,得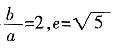 。
。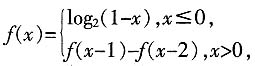 的值为
的值为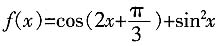 。
。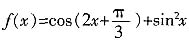 ,化简为
,化简为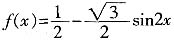 ,所以函数f(x)的最大值为
,所以函数f(x)的最大值为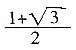 ,最小正周期π。
,最小正周期π。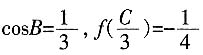 ,且C为锐角,求sinA。
,且C为锐角,求sinA。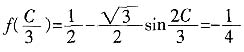 ,所以
,所以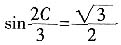 ,因为C为锐角,所以
,因为C为锐角,所以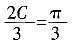 ,所以
,所以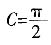 ,因此
,因此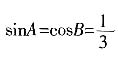 。
。
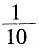 和p。
和p。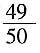 ,求p的值;
,求p的值;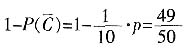
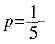
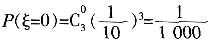
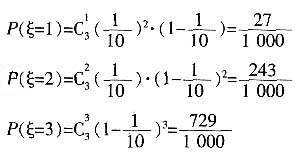

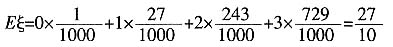
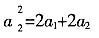 ②
②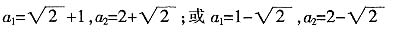
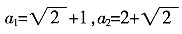 ;或
;或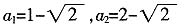
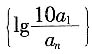 的前n项和为Tn,当n为何值时,Tn最大?并求出Tn的最大值。
的前n项和为Tn,当n为何值时,Tn最大?并求出Tn的最大值。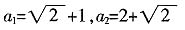
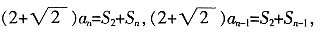
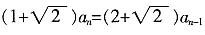 ,即
,即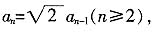
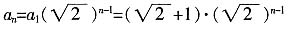
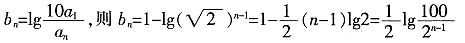
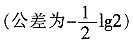 ,从而
,从而