银符考试题库B12
现在是:
试卷总分:100.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
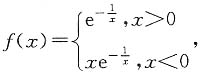 则
则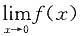 不存在的原因是______.
不存在的原因是______.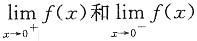 都存在但不相等
都存在但不相等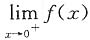 不存在
不存在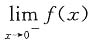 不存在
不存在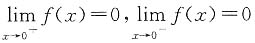 ,但f(x)在x=0处无意义,所以极限不存在,因此答案为B.
,但f(x)在x=0处无意义,所以极限不存在,因此答案为B.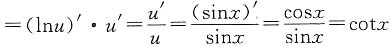 .
. =______.
=______.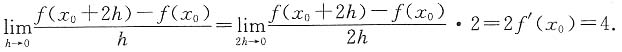
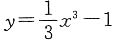 ,其过点(1,-1)的切线方程为______.
,其过点(1,-1)的切线方程为______.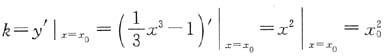 .(x0,y0)与(1,-1)均是切线上的点,故
.(x0,y0)与(1,-1)均是切线上的点,故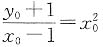 ,又因为(x0,y0)是曲线上的点,则
,又因为(x0,y0)是曲线上的点,则 -1,将其代入前式求得,x0=0或
-1,将其代入前式求得,x0=0或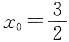 ,经检验,x0=0不合题意,舍去,故
,经检验,x0=0不合题意,舍去,故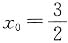 ,所以切线方程为
,所以切线方程为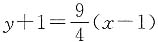 ,整理得9x-4y-13=0.
,整理得9x-4y-13=0.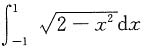 =______.
=______.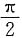
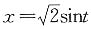 ,当x=-1时,
,当x=-1时,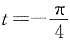 ,当x=1时,
,当x=1时, ,即原式
,即原式
 =______.
=______.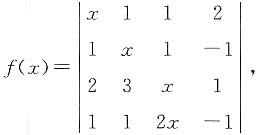 则x3的系数为______.
则x3的系数为______.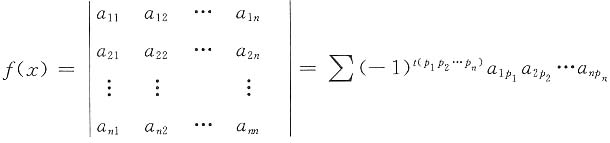 可知,含有x3的项只有两项,分别是(-1)τ(1234)a11a22a33a44=x·x·x·1=x3,(-1)τ(1243)a11a22a34a43=(-1)·x·x·1·2x=-2x3,故x3的系数为1-2=-1.
可知,含有x3的项只有两项,分别是(-1)τ(1234)a11a22a33a44=x·x·x·1=x3,(-1)τ(1243)a11a22a34a43=(-1)·x·x·1·2x=-2x3,故x3的系数为1-2=-1. 则R(A)=______.
则R(A)=______.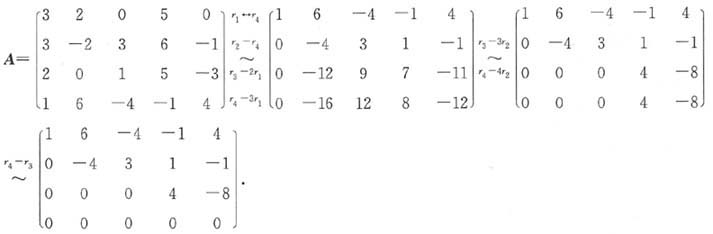
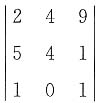
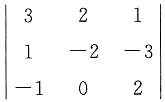 =______.
=______.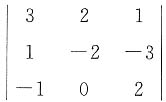 =3×(-2)×2+1×0×1+2×(-3)×(-1)-(-1)×(-2)×1-1×2×2-3×0×(-3)=-12.
=3×(-2)×2+1×0×1+2×(-3)×(-1)-(-1)×(-2)×1-1×2×2-3×0×(-3)=-12.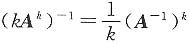 ,故C项错误;D项,(A*)*=|A|n-2A,故D项错误.所以本题选B.
,故C项错误;D项,(A*)*=|A|n-2A,故D项错误.所以本题选B. 则AT的秩是______.
则AT的秩是______.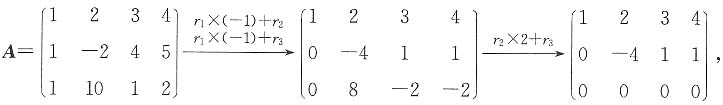 故r(A)=2,所以r(AT)=r(A)=2.
故r(A)=2,所以r(AT)=r(A)=2.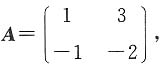 则f(A)=______.
则f(A)=______.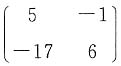
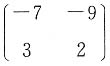
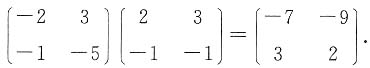
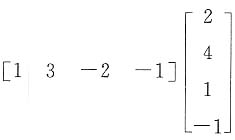 =______.
=______.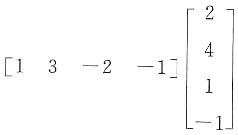 =1×2+3×4+(-2)×1+(-1)×(-1)=13.
=1×2+3×4+(-2)×1+(-1)×(-1)=13.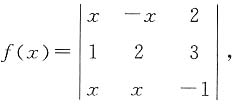 下列说法正确的是______.
下列说法正确的是______. 的二次函数
的二次函数 =-2x+2x-3x2-4x-x-3x2=-6x2-5x,令f(x)=0,得x1=0,
=-2x+2x-3x2-4x-x-3x2=-6x2-5x,令f(x)=0,得x1=0,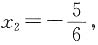 所以f(x)有两个零点,且f(x)的对称轴为
所以f(x)有两个零点,且f(x)的对称轴为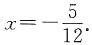 故本题选D.
故本题选D.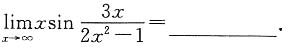
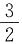
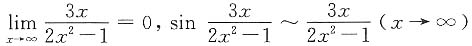 ,故有
,故有

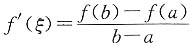 ,可得
,可得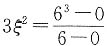 ,解得
,解得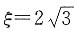 .
.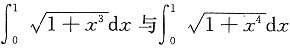 ,较小的是______.
,较小的是______.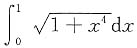
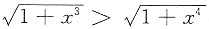 ,因此
,因此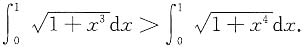
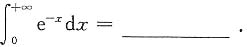
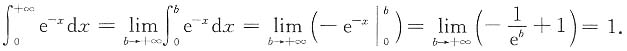
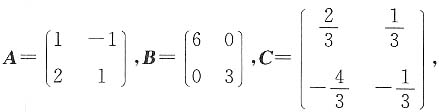 则AB9C=______.
则AB9C=______.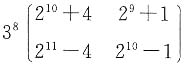
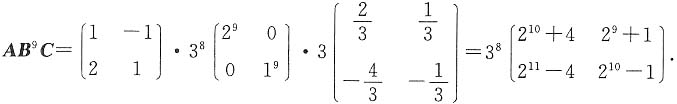
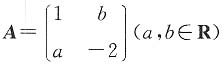 的一个特征值为3,其对应的特征向量
的一个特征值为3,其对应的特征向量 则A=______.
则A=______.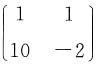
 解得
解得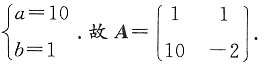
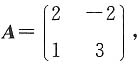 则它的特征值λ=______.
则它的特征值λ=______.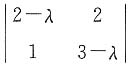 =(2-λ)(3-λ)-2=(1-λ)(4-λ),则λ1=1,λ2=4.故A的特征值为1或4.
=(2-λ)(3-λ)-2=(1-λ)(4-λ),则λ1=1,λ2=4.故A的特征值为1或4.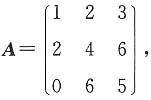 则其秩r(A)=______.
则其秩r(A)=______.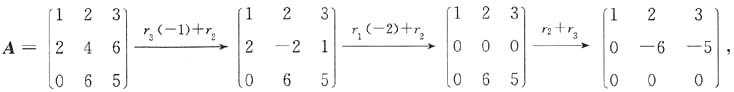 则其秩r(A)=2.
则其秩r(A)=2.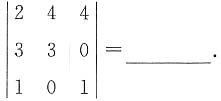
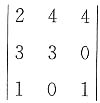 =2×3×1+3×0×4+1×4×0-4×3×1-4×3×1-2×0×0=-18.
=2×3×1+3×0×4+1×4×0-4×3×1-4×3×1-2×0×0=-18.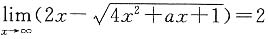 ,求a的值.
,求a的值.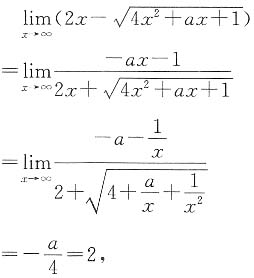
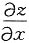 ;
;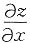 =2xex+y+x2ex+y=(x2+2x)ex+y;
=2xex+y+x2ex+y=(x2+2x)ex+y;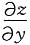 ;
;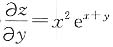 ;
;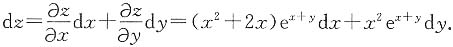
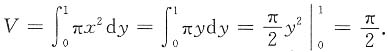
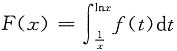 ,f(x)连续,求证
,f(x)连续,求证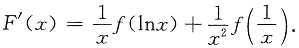

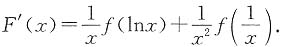
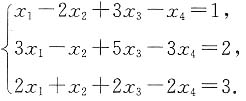
 增广矩阵
增广矩阵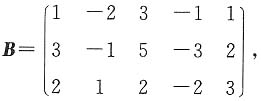
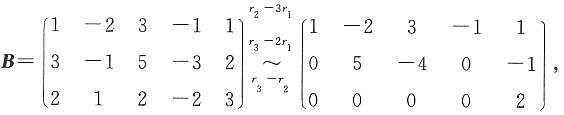
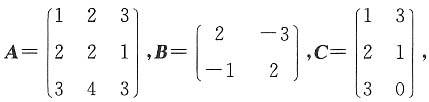 求矩阵X,使其满足AXB=C.
求矩阵X,使其满足AXB=C.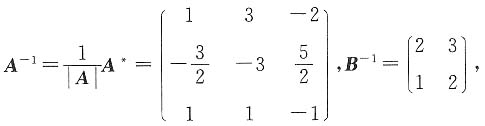
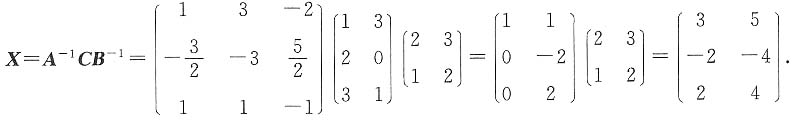
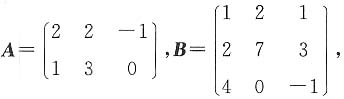 求(AB)T.
求(AB)T.