四、计算题(二)1. 已知f(x)的原函数之一为sin 3x,求∫f'(x)dx.
由sin 3x是f(x)的原函数之一,得(sin 3x)'=f(x),所以f(x)=3cos 3x.
∫f'(x)dx=f(x)+C=3cos 3x+C.
[解析] 熟练掌握原函数与积分学之间的关系,并能活用.
2. 计算
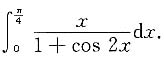
[解析] 三角函数的积分计算要掌握其基本计算公式,切不可盲目计算.
3.
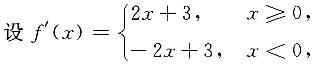
且f(2)=15,求f(x).

由f(x)为原函数,故必连续,即f(0
+)=f(0)=C
1=f(0
-)=C
2.
由f(2)=2
2+3×2+C
1=15,得C
1=5,
故
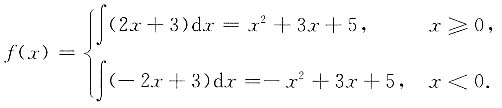
[解析] 由原函数来判断函数的连续性是此题的重点.
4. 设f(x)在(-∞,+∞)上连续,且是周期为T的函数,证明:
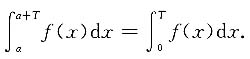
[解析] 连续周期函数在一个长度为一个周期的区间上积分是定值.
五、综合题1. 求由椭圆
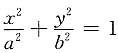
绕x轴旋转一周而成的旋转体(称旋转椭球体)的体积.
旋转椭球体可看做是由上半个椭圆
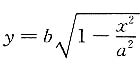
及x轴围成的图形绕x轴旋转而成的旋转体.如下图所示.
取x为积分变量,积分区间为[-a,a],于是,旋转椭球体的体积
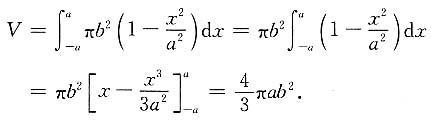
[解析] 利用积分求平面图形的面积或体积是积分学在实际生活中的广泛应用.旋转体的体积公式是需要牢记的.
2. 实验得出,在给定时刻t,镭的衰变速率(质量减少的即时速度)与镭的现存量M=M(t)成正比.又当t=0时,M=M
0,求镭的存量与时间t的函数关系.
依题意,有
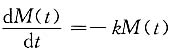
,k>0,并满足初始条件
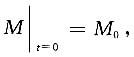
该方程是可分离变量的,分离变量后得
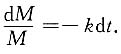
两边积分,得ln M=-kt+ln C,即M=Ce
-kt.
将初始条件M|
t=0=M
0代入上式,得C=M
0,故镭的衰变规律可表示为
M=M
0e
-kt.
[解析] 分离变量方程的初值问题.
3. 求微分方程(y
2-6x)y'+2y=0满足初始条件y|
x=2=1的特解.
这个方程不是未知函数y与y'的线性方程,但是可以将它变形为
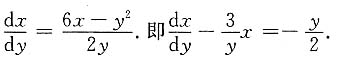
若将x视为y的函数,则对于x(y)及其导数
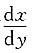
而言,上述方程是一个线性方程,由通解公式得
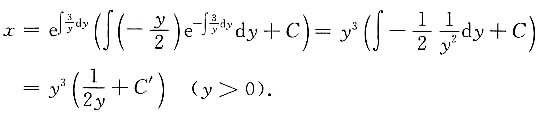
将当x=2时,y=1代入,得
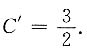
因此,所求特解为
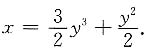
[解析] 熟练掌握线性方程的通解公式,并能活用.
4. 求解微分方程
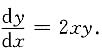
原微分方程可以分离变量,分离变量后得
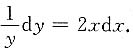
两边积分
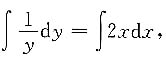
解得ln |y|=x
2+C
1,
即|y|=e
x2+C1=e
C1·e
x2,
整理得y=±e
C1·e
x2,
因为±e
C1仍是任意常数,把它记为C,便得原方程的通解为y=Ce
x2.
[解析] 可分离变量的微分方程的通用解题方法是对方程两边进行积分.
5. 估计定积分
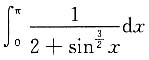
的值.
因为当x∈[0,π]时,0≤sin x≤1,所以
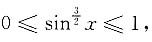
由此有
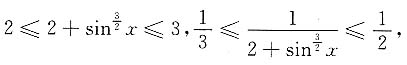
于是由估值定理有
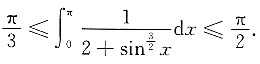
[解析] 熟练应用估值定理.
6. 比较定积分
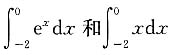
的大小.
令f(x)=e
x-x,x∈[-2,0].
因为:f'(x)=e
x-1<0,x∈(-2,0),所以f(x)在[-2,0]单调递减,
故在[-2,0]上,f(x)≥f(0)=1>0,即f(x)>0.
由性质4,有
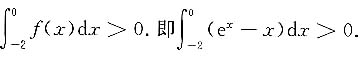
故
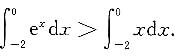
[解析] 判断函数的单调性是此题的基础.
7.

设
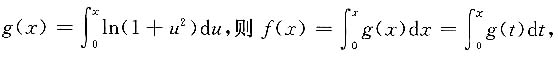
所以
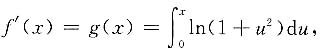
f"(x)=g'(x)=ln(1+x
2).
[解析] 熟练掌握积分与微分的关系和计算方法.
8. 利用定积分求极限:
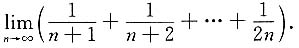
把此极限式化为某个积分和的极限式,并转化为计算定积分.为此作如下变形:
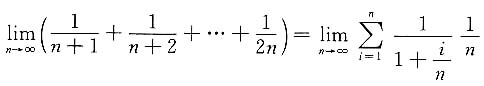
不难看出,其中的和式是函数
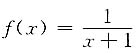
在区间[0,1]上的一个积分和(这里所取的是等分分割,
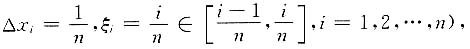
所以
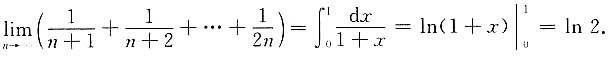
[解析] 这类问题的解题思想是要把所求的极限转化为某个函数f(x)在某区间[a,b]上的积分和的极限,然后利用牛顿-莱布尼茨公式计算
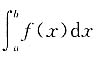
的值.