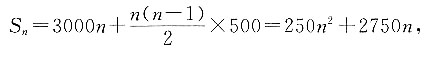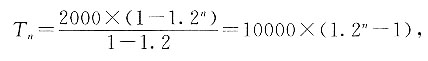一、单项选择题1. 数列
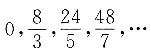
的一个通项公式为______.
A.
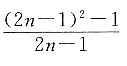
B.
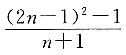
C.
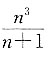
D.
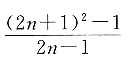
A B C D
A
[解析] 观察从第二项起数列中数字的分母可发现,他们分别是3、5、7…,即全部都是奇数,满足2n-1.分析分子与分母的关系可发现8=3
2-1,24=5
2-1,48-7
2-1,即分子与n的关系可表述为(2n-1)
2-1,故此数列的一个通项公式为
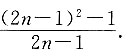
本题也可直接将n=1,2,3,4代入选项,很容易得出只有A项公式前四项与题干所给数字相同.故本题选A.
2. 已知等差数列{a
n},若满足a
1+a
2+…+a
25=380,a
26+a
27+…+a
50=1130,则a
1=______.
A B C D
C
[解析] 已知此数列为等差数列,则a
26-a
1=(a
1+25d)-a
1=25d,同理可知a
27-a
2=(a
1+26d)-(a
1+d)=25d,依此规律将题中两式相减,可得25×25d=1130-380=750,解得d=1.2.
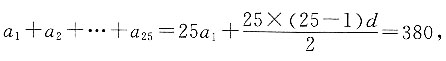
解得a
1=0.8.
3. 已知数列{a
n}是等差数列,且满足a
1+a
2+a
3=6,a
4+a
5+a
6=33,则S
10=______.
A B C D
B
[解析] 数列{a
n}是等差数列,则a
1+a
2+a
3=3a
2=6,a
2=2.a
4+a
5+a
6=3a
5=33,a
5=11.根据等差数列的性质可知,a
5-a
2=3d=11-2,则d=3,因此a
1=a
2-d=-1,所以
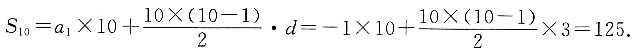
4. 已知数列{a
n}是各项均为正数的等比数列,且a
3·a
8=4,则log
2a
1+log
2a
2+…+log
2a
10=______.
A B C D
D
[解析] 因为数列{a
n}为各项均为正数的等比数列,所以
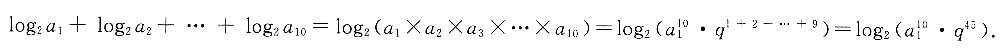
因为a
3·a
8=4,即
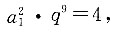
所以
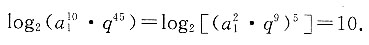
6. 若{a
n}为公差不为零的等差数列,且满足
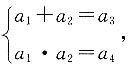
则a
5=______.
A B C D
C
[解析] 因为{a
n}为等差数列,则设a
n=a
1+(n-1)d,题中方程组即为
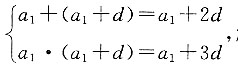
解得
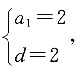
即{a
n}为首项和公差均为2的等差数列,a
5=a
1+4d=10.
7. 下列四个数字中,有三个可与
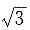
组成一个等比数列,则不属于这个等比数列的一项是______.
A.
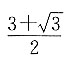
B.
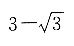
C.
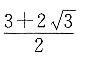
D.
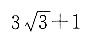
A B C D
D
[解析] 已知等比数列中的一项是

,则根据公比不变可检验数字是否属于此等比数列.
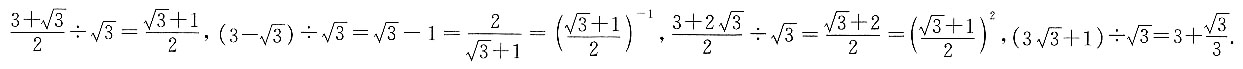
计算可知,A、B、C项与
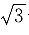
的商均为
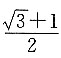
的倍数,即公比为
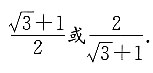
这个争此数列的项为
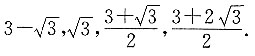
因此D项不属于这个数列.
8. 已知等比数列{a
n}的公比为
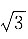
,则
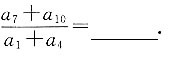
A.
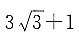
B.3
C.9
D.27
A B C D
D
[解析] 根据等比数列性质可知,
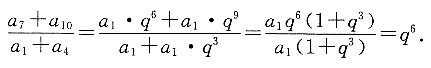
已知公比为
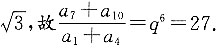
9. 方程x
2-20x+16=0有两个不相等的实数根,若这两根是等差数列中的两项,则其等差中项是______,若这两根是等比数列中的两项,则其等比中项是______.
A B C D
D
[解析] 已知方程为x
2-20x+16=0,则x
1+x
2=20,x
1x
2=16.若x
1、x
2为等差数列中的两项,则其等差中项为
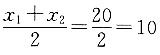
;若x
1、x
2为等比数列中的两项,则其等比中项为
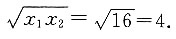
10. 已知方程(x
2-2x+m)(x
2+2x+n)=0的四个不相等的实数根可组成一个等差数列,且数列第三项为
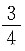
,则这个等差数列的第四项的值是______.
A.
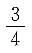
B.
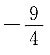
C.
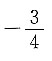
D.
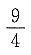
A B C D
D
[解析] 方程有四个不相等的实数根,设为x
1、x
2,x
3、x
4,则
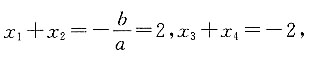
因此这四个数的和为0.设第一项为
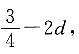
第二项为
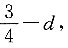
第四项为
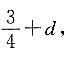
则
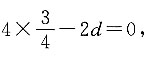
解得
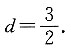
则第四项为
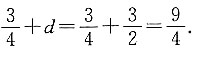
11. 设S
n是等差数列{a
n}的前n项和,已知a
3=16.5,a
8=54,则S
8=______.
A B C D
A
[解析] 因为数列{a
n}为等差数列,所以a
8-a
3=5d=54-16.5,所以d=7.5.a
3=a
1+2d=16.5,所以
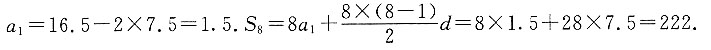
12. 若数列{a
n}是等比数列,则公比q>1是a
3>a
2>a
1的______.
- A.充分条件
- B.充要条件
- C.必要条件
- D.既不充分也不必要条件
A B C D
D
[解析] a
n=a
1·q
n-1,要使a
3>a
2>a
1成立,需要使a
1·q
2>a
1·q>a
1,是否成立同时取决于a
1和q的值.若一个数列q=2,a
1=-1,则a
3<a
2<a
1.若一个数列中a
3>a
2>a
1,当a
1=-1,
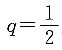
是成立的.所以公比q>1是a
3>a
2>a
1的既不充分也不必要条件.
13. 若数列{a
n}的各项满足a
n+1=2a
n-n+1,则下列说法中正确的是______.
- A.数列{an}为等差数列
- B.数列{an-n}为等差数列
- C.数列{an+n}为等比数列
- D.数列{an-n}为等比数列
A B C D
D
[解析] 已知a
n+1=2an-n+1,则可将等式转换为a
n+1=2a
n-2n+n+,a
n+1-n-1=2(a
n-n),

即数列{a
n-n}为等比数列,公比为2.
二、填空题1. 数列{b
n}的前n项和公式为S
n=n
2-2n,则此数列的通项公式b
n=______.
2n-3
[解析] 当n=1时,S1=b1=1-2=-1;当n≥2时,bn=Sn-Sn-1=n2-2n-(n-1)2+2(n-1)=2n-3.将n=1代入通项公式得b1=2-3=-1,符合通项公式,所以bn=2n-3.
2. 已知数列{a
n}的通项公式a
n=2n+ln(n+1),数列{b
n}的通项公式b
n=a
n+1-a
n,则数列{b
n}的前n项和S
n=______.
[解析]
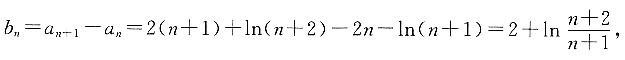
则前n项和
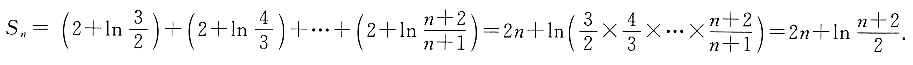
3. 设数列{a
n}的前n项和公式为
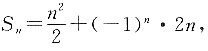
则a
8=______.
37.5
[解析] 根据数列的性质可知,
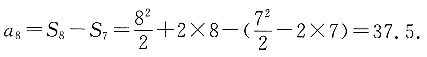
4. 设数列{b
n}的通项公式b
n=An
2+B,且满足
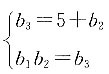
,则代数式A+B=______.
2或-4
[解析] 已知b
n=An
2+B,则b
1=A+B,b
2=4A+B,b
3=9A+B,将各项的值代入
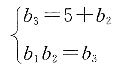
中,可得
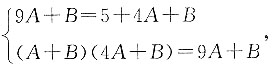
解得A=1,B=1或-5.所以A+B=2或A+B=-4.
5. 在
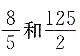
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积是______.
1000
[解析] 设插入的三个数分别为a、b、c,则根据等比数列的性质可知
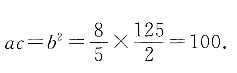
若公比为负数,则a、c为负,b为正;若公比为正数,则a、b、c均为正,所以b=10,故abc=100×10=1000.
6. 已知数列a,5,b既是等差数列又是等比数列,则其公差是______,其公比是______.
0 1
[解析] 因为数列a,5,b既是等差数列又是等比数列,则满足
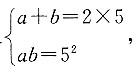
解得a=b=5,数列的公差d=5-5=0,公式
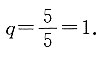
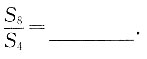
7. 已知数列{a
n}为公比大于1的等比数列,且满足9a
3-a
5=0,则
82
[解析] 已知数列{a
n}为等比数列,则9a
3-a
5=9×a
1q
2-a
1q
4=0,因为数列{a
n}公比大于1,所以

8. 设S
n是等比数列{a
n}的前n项和,且满足6S
7=a
8+6,6S
6=a
7+6,则此数列的公比为______.
7
[解析] 根据数列的性质可知,a
7=S
7-S
6,则6(S
7-S
6)=(a
8+6)-(a
7+6),6a
7=a
8-a
7,即
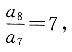
所以此数列的公比为7.
9. 设数列{a
n}为等比数列,若a
1999和a
2000分别为方程4x
2-8x+3=0的两根,则a
2001+a
2002=______.
[解析] 解方程4x
2-8x+3=0可得
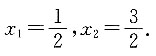
若
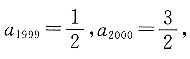
则

,即
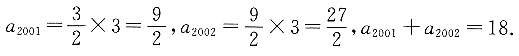
若
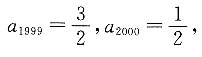
则
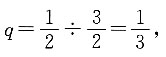
即
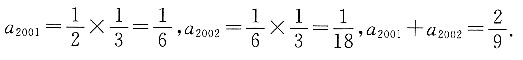
10. 已知数列1,2,2,3,3,3,4,4,4,4,…,则数字12第一次出现是在第______项.
67
[解析] 根据题意可知,数字1第一次出现是在第1项;数字2第一次出现是在第2项;数字3第一次出现是在第4项,数字4第一次出现是在第7项.用n来表示数字,用a
n来表示数字第一次出现时的项数.依据题中规律可得到:a
n-a
n-1=n-1,a
n-1-a
n-2=n-2,…,a
2-a
1=1.各项左右相加,可得
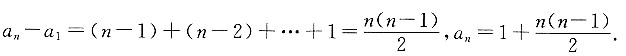
当n=12时,a
12=67.
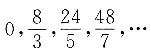 的一个通项公式为______.
的一个通项公式为______.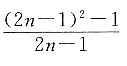
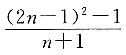
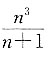
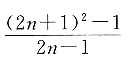
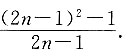 本题也可直接将n=1,2,3,4代入选项,很容易得出只有A项公式前四项与题干所给数字相同.故本题选A.
本题也可直接将n=1,2,3,4代入选项,很容易得出只有A项公式前四项与题干所给数字相同.故本题选A.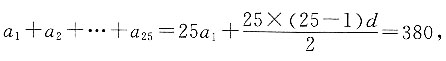 解得a1=0.8.
解得a1=0.8.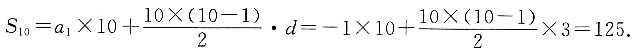
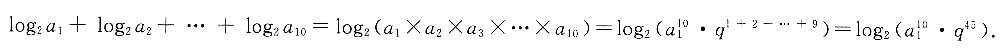 因为a3·a8=4,即
因为a3·a8=4,即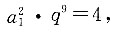 所以
所以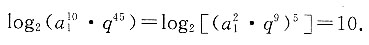
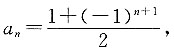 也可以是
也可以是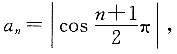 故B项错误;数列具有有序性,如数列1,2,3与数列3,2,1不是同一数列,故C项错误;有的数列的项与项数之间不存在对应的通项公式,如数列1,3,8,3,2,5无通项公式,D项错误.
故B项错误;数列具有有序性,如数列1,2,3与数列3,2,1不是同一数列,故C项错误;有的数列的项与项数之间不存在对应的通项公式,如数列1,3,8,3,2,5无通项公式,D项错误.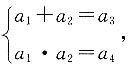 则a5=______.
则a5=______.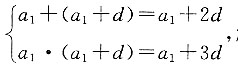 解得
解得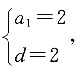 即{an}为首项和公差均为2的等差数列,a5=a1+4d=10.
即{an}为首项和公差均为2的等差数列,a5=a1+4d=10.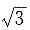 组成一个等比数列,则不属于这个等比数列的一项是______.
组成一个等比数列,则不属于这个等比数列的一项是______.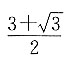
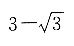
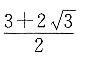
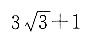
 ,则根据公比不变可检验数字是否属于此等比数列.
,则根据公比不变可检验数字是否属于此等比数列.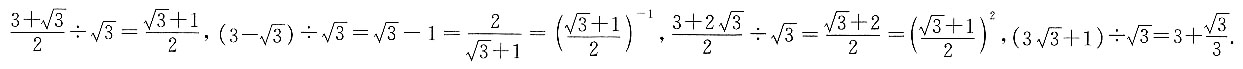 计算可知,A、B、C项与
计算可知,A、B、C项与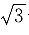 的商均为
的商均为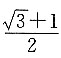 的倍数,即公比为
的倍数,即公比为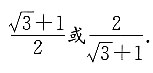 这个争此数列的项为
这个争此数列的项为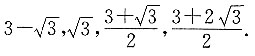 因此D项不属于这个数列.
因此D项不属于这个数列.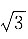 ,则
,则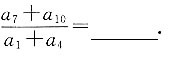
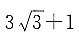
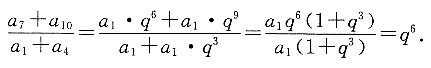
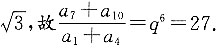
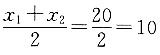 ;若x1、x2为等比数列中的两项,则其等比中项为
;若x1、x2为等比数列中的两项,则其等比中项为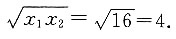
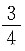 ,则这个等差数列的第四项的值是______.
,则这个等差数列的第四项的值是______.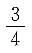
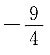
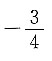
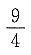
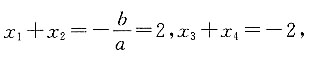 因此这四个数的和为0.设第一项为
因此这四个数的和为0.设第一项为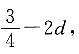 第二项为
第二项为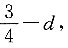 第四项为
第四项为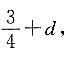 则
则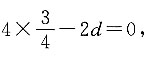 解得
解得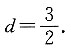 则第四项为
则第四项为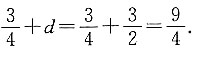
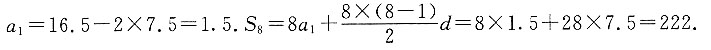
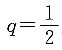 是成立的.所以公比q>1是a3>a2>a1的既不充分也不必要条件.
是成立的.所以公比q>1是a3>a2>a1的既不充分也不必要条件. 即数列{an-n}为等比数列,公比为2.
即数列{an-n}为等比数列,公比为2.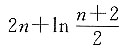
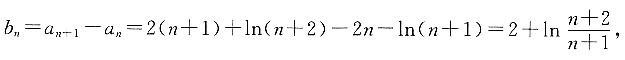 则前n项和
则前n项和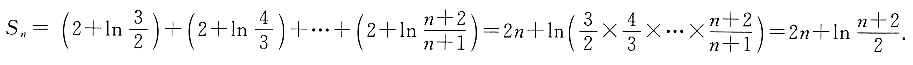
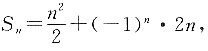 则a8=______.
则a8=______.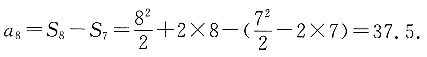
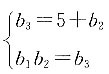 ,则代数式A+B=______.
,则代数式A+B=______.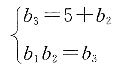 中,可得
中,可得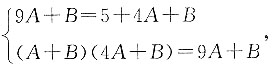 解得A=1,B=1或-5.所以A+B=2或A+B=-4.
解得A=1,B=1或-5.所以A+B=2或A+B=-4.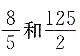 之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积是______.
之间插入三个数,使这五个数成等比数列,则插入的三个数的乘积是______.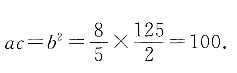 若公比为负数,则a、c为负,b为正;若公比为正数,则a、b、c均为正,所以b=10,故abc=100×10=1000.
若公比为负数,则a、c为负,b为正;若公比为正数,则a、b、c均为正,所以b=10,故abc=100×10=1000.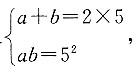 解得a=b=5,数列的公差d=5-5=0,公式
解得a=b=5,数列的公差d=5-5=0,公式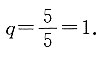


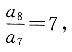 所以此数列的公比为7.
所以此数列的公比为7.
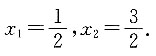 若
若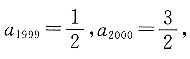 则
则 ,即
,即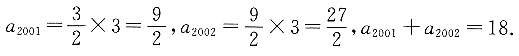 若
若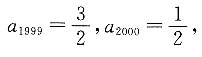 则
则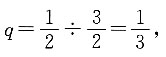 即
即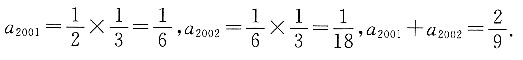
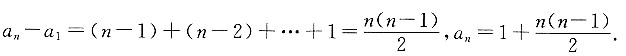 当n=12时,a12=67.
当n=12时,a12=67.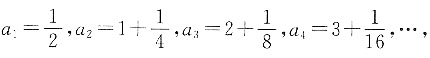 则依此规律求:
则依此规律求: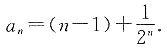
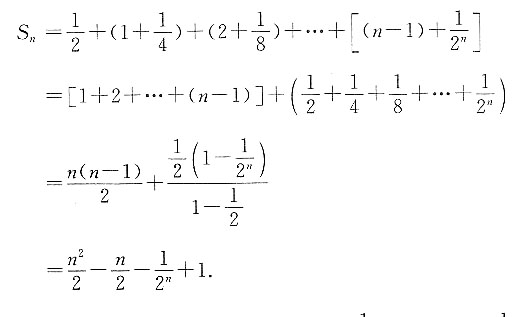
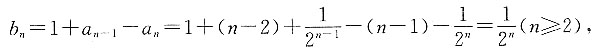
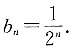
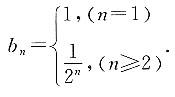
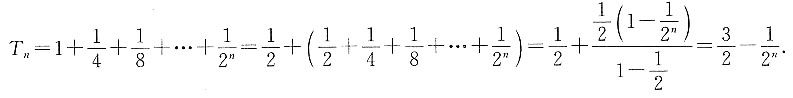
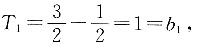 即n=1也符合此求和公式,
即n=1也符合此求和公式,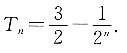
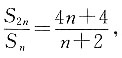 求:
求: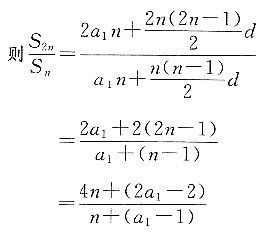
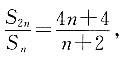
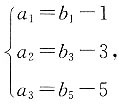 求等差数列{bn}的公差d.
求等差数列{bn}的公差d.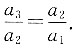
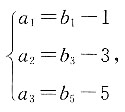
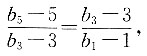
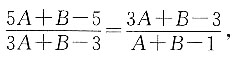
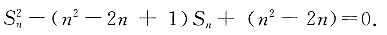
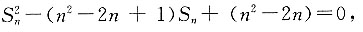
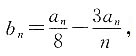 则{bn}中任意一项均大于-4.
则{bn}中任意一项均大于-4.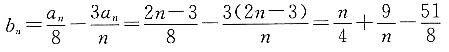

 则求:
则求: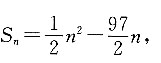
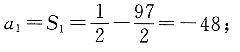
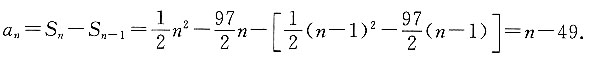

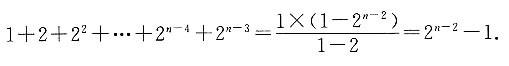

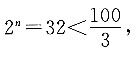
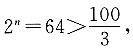 故可知,数列{bn}中小于100的项有5个.
故可知,数列{bn}中小于100的项有5个.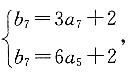
 则求数列{an}的通项公式.
则求数列{an}的通项公式.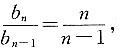 且点(an,bn)在直线y=3x+2上,即bn=3an+2,则
且点(an,bn)在直线y=3x+2上,即bn=3an+2,则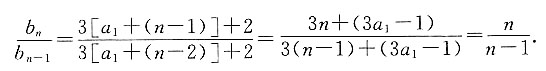
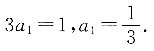
 为首项,1为公差的等差数列,
为首项,1为公差的等差数列,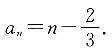
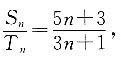 求
求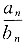 的最大值.
的最大值.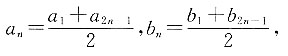
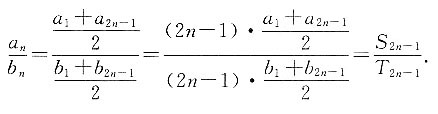
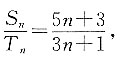
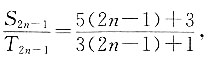
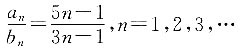
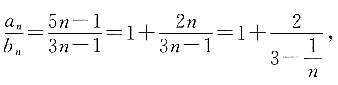 则
则 值随n值增大而减小,
值随n值增大而减小,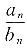 有最大值,最大值为2.
有最大值,最大值为2.