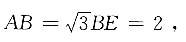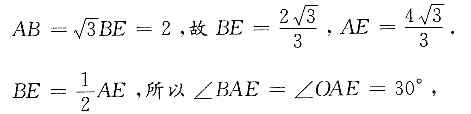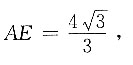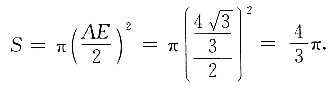一、单项选择题1. 已知空间内两直线
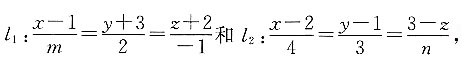
若l
1//l
2,则______.
A.
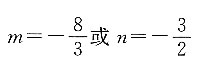
B.
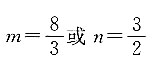
C.
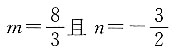
D.
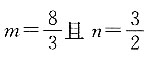
A B C D
D
[解析] 由题意知直线l
1,l
2的方向向量分别为s
1=(m,2,-1),s
2=(4,3,-n),因为l
1//l
2,所以
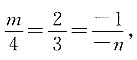
解得
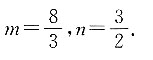
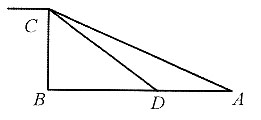
11. 如图所示,一小船在离岸边12米处由岸上拉索拉靠岸.已知岸高5米,当拉索向前进了5米时,小船向前行驶了______米.
A.
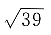
B.7
C.
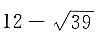
D.5
A B C D
C
[解析] 设小船在A地时,距离岸边B为12米,岸高BC=5米,所以拉索
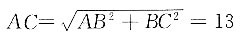
米;当拉索向前进了5米时,小船行驶到D地,此时CD=13-5=8米,所以
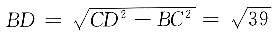
米,则小船前进了
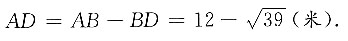
16. 如图所示,
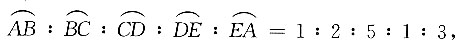
下列说法正确的是______.
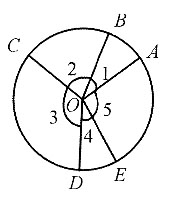
①∠1+∠2=∠5;
②∠3=45°,∠5=75°;
③2∠4=∠2;
④∠5=∠2+∠3.
A B C D
B
[解析] 依题意可知∠1:∠2:∠3:∠4:∠5=1:2:5:1:3,所以
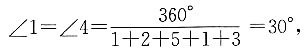
∠2=2∠1=60°,∠3=5∠1=150°,∠5=3∠1=90°.因此①③正确,②④错误,故本题选B.
18. 已知⊙O
1和⊙O
2外切于点M,其面积之比为9:25.延长⊙O
1的弦AM交⊙O
2于B,已知O
1不在弦MA上,则______.
- A.5MA=3MB
- B.25MA=9MB
- C.3MA=5MB
- D.9MA=25MB
A B C D
A
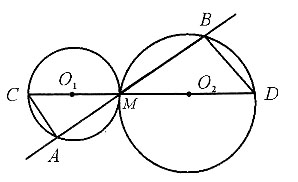
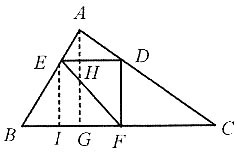
[解析] 如图,连接O
1O
2,并将其延长,分别交⊙O
1和⊙O
2于C和D,易知MC和MD分别是⊙O
1和⊙O
2的直径.连接AC、BD,易证Rt△AMC∽Rt△BMD,所以
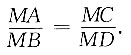
又因为S
⊙O1:S
⊙O2=9:25,故r
1:r
2=3:5,即
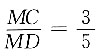
,所以
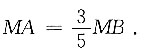
二、填空题1. 已知数列{a
n}为a
1=1且公差不为0的等差数列,向量p=(a
1,a
2,a
3),q=(a
2,a
6,a
10).若p//q,则a
n的通项公式是______.
an=3n-2
[解析] 根据题意可设数列{a
n}的通项公式为a
n=1+(n-1)d.因为p//q,所以
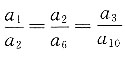
,即
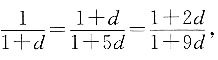
解得d=3或0(舍去).因此a
n=3n-2.
2. 已知

则a与b的夹角为______.
[解析] |a-b|
2=(a-b)
2=a
2-2a·b+b
2=1-2a·b+4=3,所以a·b=1,故
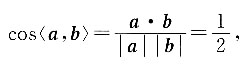
所以a与b的夹角为
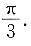
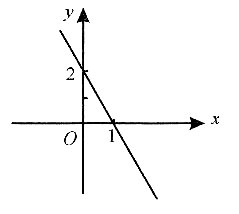
3. 已知向量a=(3,4,5),则与a平行的单位向量n=______.
[解析]
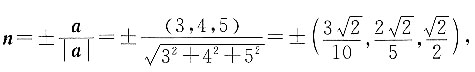
所以与向量a平行的单位向量为
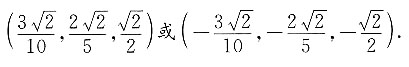
4. 已知空间中三个向量a=(2,1,-1),b=(-1,3,2),c=(2,-2,1),则(a×b)·c=______.
23
[解析] (a×b)·c=(1×2-(-1)×3,(-1)×(-1)-2×2,2×3-1×(-1))·(2,-2,1)=(5,-3,7)·(2,-2,1)=23.
5. 若向量m,n的夹角为60°,
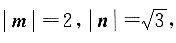
则(m+2n)(m-n)=______.
[解析]
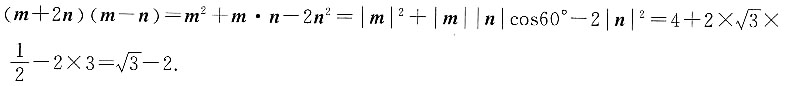
6. 已知空间两直线
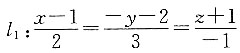
和

则直线l
1,l
2的夹角的余弦值是______.
[解析] 依题意可知直线l
1,l
2的方向向量分别是
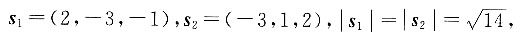
所以直线l
1,l
2的夹角的余弦值
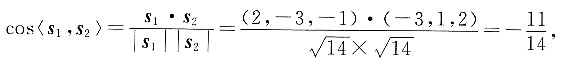
又因为两直线的夹角范围为

所以直线l
1与l
2夹角的余弦值为
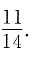
7. 已知a⊥b,|a|=2,|b|=4,则|a+b|______|a-b|.(填“>”“<”或“=”)
=
[解析] 依题意知a·b=0,所以
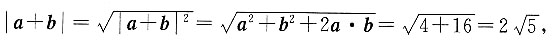
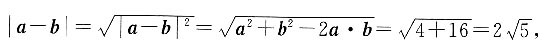
所以|a+b|=|a-b|.
8. 已知向量a=2i+3j-k,b=-i+2j-2k,c=2ma-3nb,若c⊥x轴,则m=______.(用n表示)
[解析] 依题意有c=2m(2i+3j-k)-3n(-i+2j-2k)=(4m+3n)i+(6m-6n)j-(2m-6n)k,取x轴单位方向向量e=(1,0,0),因为c⊥x轴,所以c⊥e,即c·e=(4m+3n,6m-6n,-2m+6n)·(1,0,0)=4m+3n=0,所以
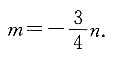
9. 平行四边形、菱形、正方形、长方形均为对称图形,其分别有______条、______条、______条、______条对称轴.
0 2 4 2
[解析] 平行四边形是中心对称图形,没有对称轴;菱形、正方形、长方形既是中心对称图形又是轴对称图形,其中菱形的两条对角线是其对称轴,长方形的长和宽对折的两条折痕即为其对称轴,正方形的两条对角线和对边对折的两条折痕共四条对称轴.
10. 四边形ABCD是如图所示扇形中的矩形,当矩形面积最大时,阴影部分的面积为______.
[解析] 连接DB,设∠BDC=θ,则DB=r,BC=rsinθ,DC=rcosθ,S
矩形=DC·BC=r
2·sinθcosθ=
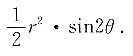
因为
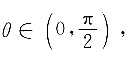
则2θ∈(0,π),当
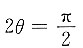
时,sin2θ=1,取最大值.此时
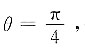
矩形为正方形.此时
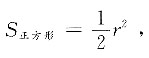
所以
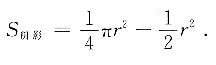
11. 已知⊙O,⊙P的半径分别为6和8,两圆心距离为d.当两圆相交时,d的取值范围是______;当两圆相切时,d的取值是______;当两圆相离时,d的取值范围是______.
2<d<14;2或14;0<d<2或d>14
[解析] 当d=6+8=14时,两圆外切,当d=8-6=2时,两圆内切;当2<d<14时,两圆相交;相离有两种情况—内含与外离,当0<d<2时,两圆内含,当d>14时,两圆外离.
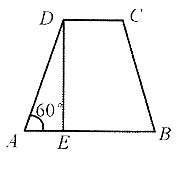
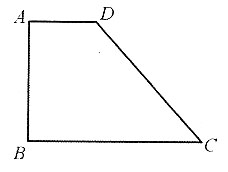
12. 已知等腰梯形ABCD,其下底AB=6,AD=DC,∠A=60°,则该梯形的面积为______.
[解析] 如图,作DE⊥AB于点E,由题意知AE=AD·cos60°,DE=AD·sin60°,AD=DC,所以AB=2AE+DC=2ADcos60°+DC=2DC=6,故
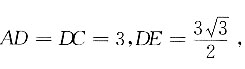
所以
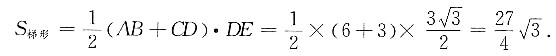
13. AB、AC是⊙O的两条相互垂直的弦,D、E分别是它们的中点,且OD=OE,则AB______AC.(填“<”“>”或“=”)
=
[解析] 如图所示,B、C连线过圆心O,因为D、E分别是AB、AC的中点,且AB⊥AC,所以OD⊥AB,OE⊥AC.又因为OD=OE,所以四边形ODAE是正方形,故有AC=2AE=2AD=AB.
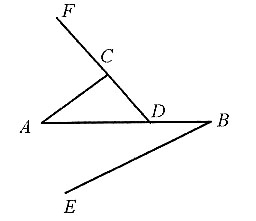
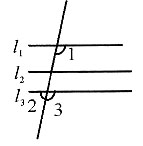
14. 如图所示,已知AC//BE,∠B=27°,∠ACF=87°,则∠ADC=______.
60°
[解析] 因为AC//BE,所以∠A=∠B=27°.由三角形的一个外角等于和它不相邻的两内角之和可知,∠ACF=∠A+∠ADC=87°,所以∠ADC=87°-27°=60°.
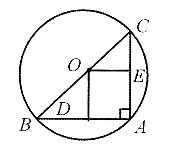
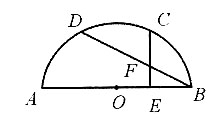
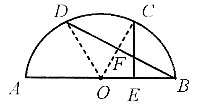
15. 如图所示,C、D是半圆上两个点,
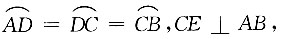
垂足为E,与BD交于F,已知
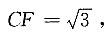
则⊙O的直径为______.
6
[解析] 如图所示,连接OC、OD,设⊙O的半径为r,因为
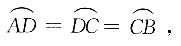
所以∠COB=∠DOA=60°,∠ABD=30°,因为CE⊥AB,OB=OC=r,所以
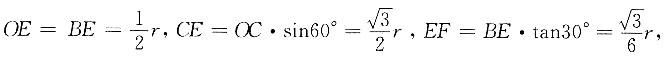
所以
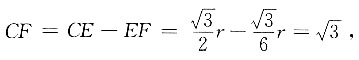
故r=3,直径d=2r=6.
三、解答题已知空间向量a=(3,0,-4),b=(2,-3,1),求:1. a·b,a×b;
a·b=(3,0,-4)·(2,-3,1)=3×2+0×(-3)+(-4)×1=2;
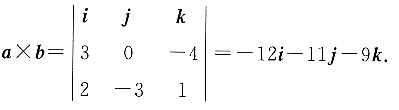
2. (2a)·(-b),(-a)×(2b);
(2a)·(-b)=-2(a·b)=-2×2=-4;
(a)×(2b)=-2(a×b)=-2(-12i-11j-9k)=24i+22j+18k.
3. 向量a,b所成角的正弦值.
因为
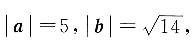
所以
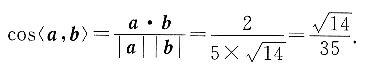
a与b的夹角在[0,π]的范围内,
所以0≤sin〈a,b〉≤1.
所以
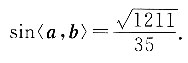
4. 过点M(-2,3,1)且与A,B,C三点所在平面平行的平面β;
设A,B,C三点所在的平面α的法向量为n=(x',y',z').
依题意知
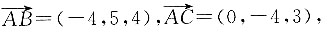
所以
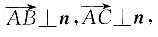
即

令z=4,代入上述方程组,解得
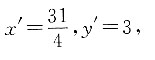
所以平面α的一个法向量为
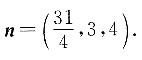
因为α//β,
所以n也是平面β的法向量,即β⊥n,
又因为平面β过点(-2,3,1),
所以平面β的方程为
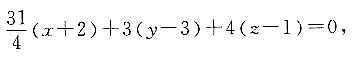
整理可得平面β的方程为31x+12y+16z+10=0.
5. 向量
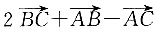
的模;
6. 点A到BC的距离.(结果用根号表示即可)
依题意可设
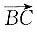
为其所在直线l的方向向量,且直线过C(-1,-3,1),
所以l的直线方程为:
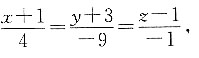
所以A到BC的距离

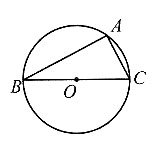
7. 直径所对应的圆周角是直角;
如图所示,BC为⊙O的直径,A为圆上不同于B、C的一点.
如图可知,
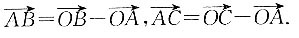
因为
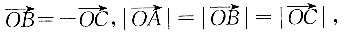
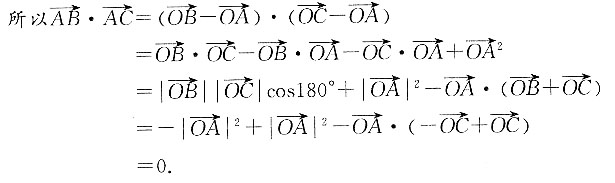
所以

即∠BAC=90°.
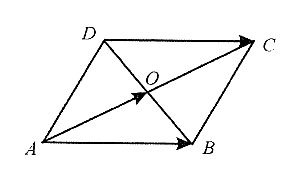
8. 平面上对角线互相平分的四边形是平行四边形.
如图所示,ABCD为四边形,O分别为AC、BD的中点.
由图可知,
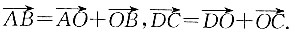
因为对角线相互平分,
所以
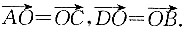
所以
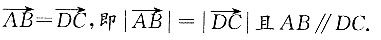
所以该四边形是平行四边形.
9. 证明:(a-b)⊥c;
因为a、b、c为单位向量,
所以|a|=|b|=|c|=1.
设a与b之间的夹角为θ,
由题干得a+b=-c,即(a+b)
2=c
2.
化简为|a|
2+2|a||b|cosθ+|b|
2=|c|
2.
代入得
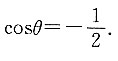
因为θ∈[0,π],所以
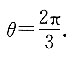
同理可求得a与c、b与c的夹角均为
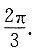
所以(a-b)·c=a·c-b·c
=1×1×cos120°-1×1×cos120°
=0.
即(a-b)⊥c.
10. 若|a-b+kc|>2(k∈R),求k的取值范围.
因为|a-b+kc|>2,
所以|a-b+kc|
2>4,即a
2+b
2+k
2c
2-2a·b+2ka·c-2kb·c>4,
因为
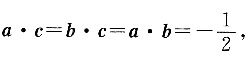
所以
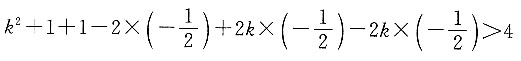
即k
2-1>0,解得k<-1或k>1.
故k的取值范围是(-∞,-1)∪(1,+∞).
11. 证明:AC=DB;
如图所示,
因为梯形是等腰梯形,
所以∠DCB=∠ABC,AB=DC,
所以△DCB≌△ABC,
因此AC=DB.
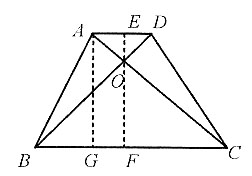
12. 若AD=2,AB=5,BC=8,求△OBC的面积.
作AG⊥BC交BC于G,过O作EF⊥BC分别交AD、BC于E、F.
因为梯形ABCD为等腰梯形,
所以
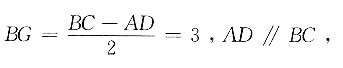
所以
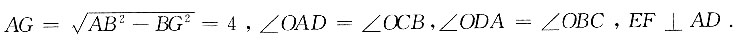
∠AOD与∠COB是对顶角,所以∠AOD=∠COB,
所以△AOD∽△COB.
因为OE、OF分别是△AOD和△COB的高,
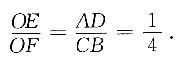
又因为AG=OE+OF=4,
所以
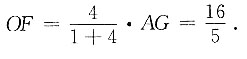
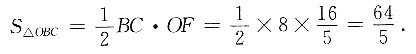
13. 小明晚上下班回家,在其正前方不远处有一6米高的路灯,此时小明身后影子长2.4米;当小明继续向前走2.45米时,小明身后的影子缩短了1.05米.问:小明身高多少?
依题意作图,
其中,AD=2.4,AB=2.45,BE=AD-1.05=1.35,CO=6.
由图可知△CDO∽△FDA,△CEO∽△GEB,
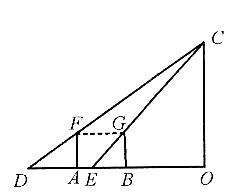
因为
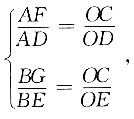
又因为AF=BG,即

解得AF=1.8,BO=3.15.
所以小明身高1.8米.
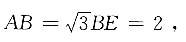

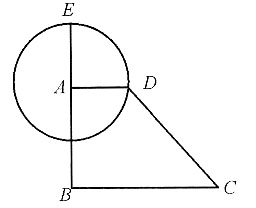
14. 证明:点O是AC的中点;
证明:因为△AOE是△ABE折叠后的图形,所以△AOE≌△ABE.
因为∠B为直角,所以∠AOE也为直角,因此∠AOE=∠COE=90°.
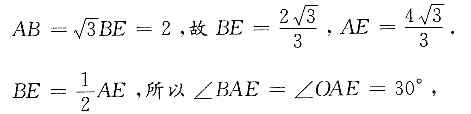
∠OCE=90°-60°=30°=∠OAE,所以△OCE≌△OAE,则AO=CO,
所以O是AC的中点.
15. 求四边形ABEO外接圆的面积.
因为∠AOE=∠ABE=90°,
根据直径对应的圆周角为直角可知,AE即为四边形ABEO外接圆的直径.
因为
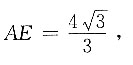
所以外接圆的面积
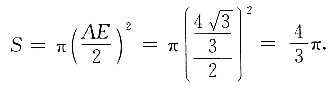
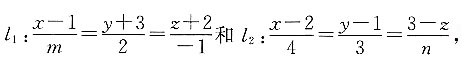 若l1//l2,则______.
若l1//l2,则______.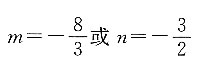
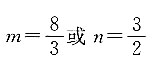
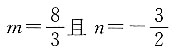
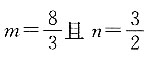
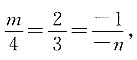 解得
解得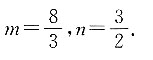
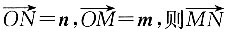 =______.
=______.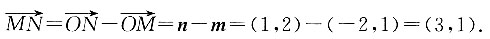

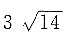
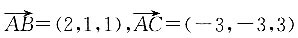 ,所以
,所以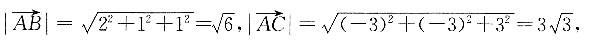
 又因为∠BAC是平行四边形的内角,所以
又因为∠BAC是平行四边形的内角,所以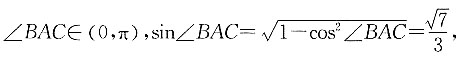
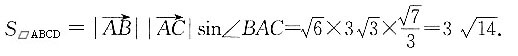
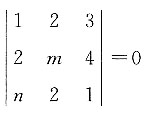 ,所以m+8n-3mn=0.
,所以m+8n-3mn=0.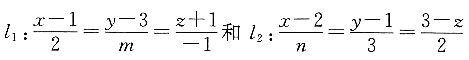 ,则“l1⊥l2”是“m=-n=-2”的______.
,则“l1⊥l2”是“m=-n=-2”的______.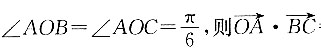 =______.
=______.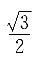

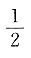
 因为
因为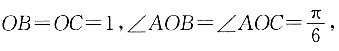 所以
所以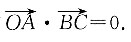

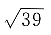
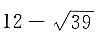
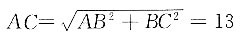 米;当拉索向前进了5米时,小船行驶到D地,此时CD=13-5=8米,所以
米;当拉索向前进了5米时,小船行驶到D地,此时CD=13-5=8米,所以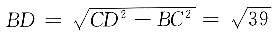 米,则小船前进了
米,则小船前进了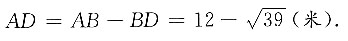

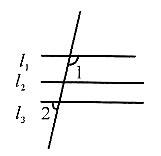
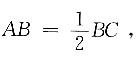 分别以AD和CD为底作平行四边形的高h1、h2,则______
分别以AD和CD为底作平行四边形的高h1、h2,则______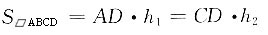 ,因为
,因为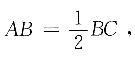 所以
所以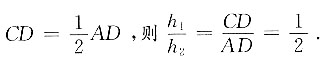
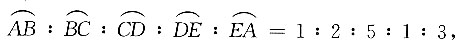 下列说法正确的是______.
下列说法正确的是______.
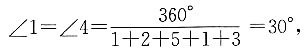 ∠2=2∠1=60°,∠3=5∠1=150°,∠5=3∠1=90°.因此①③正确,②④错误,故本题选B.
∠2=2∠1=60°,∠3=5∠1=150°,∠5=3∠1=90°.因此①③正确,②④错误,故本题选B.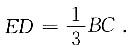 过E作EI⊥BC交BC于I,过A作AG⊥BC交BC于G,交DE于H,易知AH⊥ED,△AEH∽△EBI,因为BE=2EA,所以EI=2AH,又因为
过E作EI⊥BC交BC于I,过A作AG⊥BC交BC于G,交DE于H,易知AH⊥ED,△AEH∽△EBI,因为BE=2EA,所以EI=2AH,又因为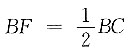 .即
.即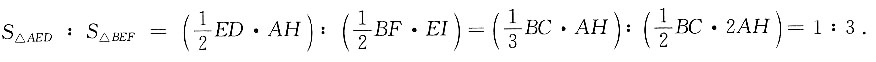
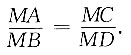 又因为S⊙O1:S⊙O2=9:25,故r1:r2=3:5,即
又因为S⊙O1:S⊙O2=9:25,故r1:r2=3:5,即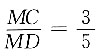 ,所以
,所以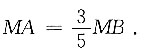

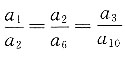 ,即
,即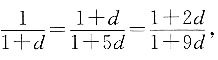 解得d=3或0(舍去).因此an=3n-2.
解得d=3或0(舍去).因此an=3n-2. 则a与b的夹角为______.
则a与b的夹角为______.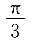
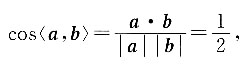 所以a与b的夹角为
所以a与b的夹角为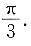
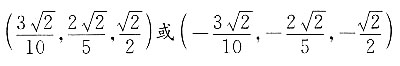
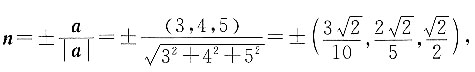 所以与向量a平行的单位向量为
所以与向量a平行的单位向量为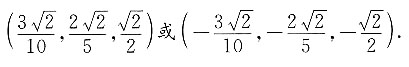
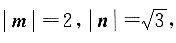 则(m+2n)(m-n)=______.
则(m+2n)(m-n)=______.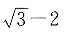
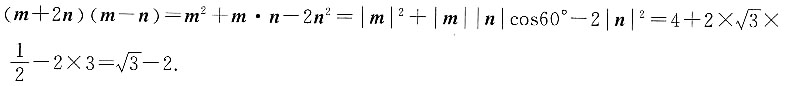
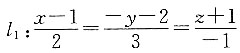 和
和 则直线l1,l2的夹角的余弦值是______.
则直线l1,l2的夹角的余弦值是______.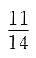
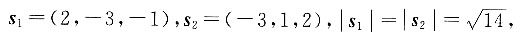 所以直线l1,l2的夹角的余弦值
所以直线l1,l2的夹角的余弦值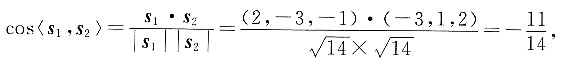 又因为两直线的夹角范围为
又因为两直线的夹角范围为 所以直线l1与l2夹角的余弦值为
所以直线l1与l2夹角的余弦值为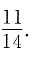
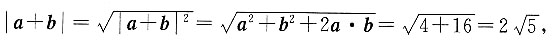
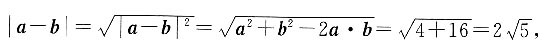 所以|a+b|=|a-b|.
所以|a+b|=|a-b|.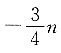
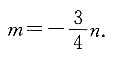
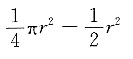
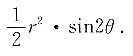 因为
因为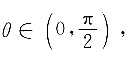 则2θ∈(0,π),当
则2θ∈(0,π),当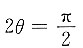 时,sin2θ=1,取最大值.此时
时,sin2θ=1,取最大值.此时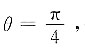 矩形为正方形.此时
矩形为正方形.此时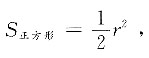 所以
所以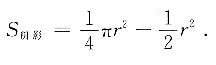
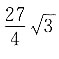
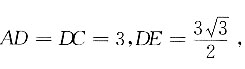 所以
所以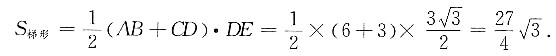



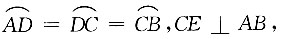 垂足为E,与BD交于F,已知
垂足为E,与BD交于F,已知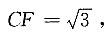 则⊙O的直径为______.
则⊙O的直径为______.
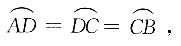 所以∠COB=∠DOA=60°,∠ABD=30°,因为CE⊥AB,OB=OC=r,所以
所以∠COB=∠DOA=60°,∠ABD=30°,因为CE⊥AB,OB=OC=r,所以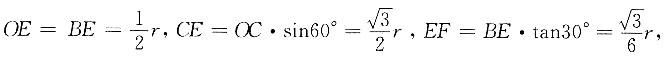 所以
所以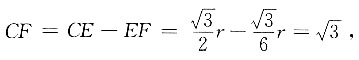 故r=3,直径d=2r=6.
故r=3,直径d=2r=6.
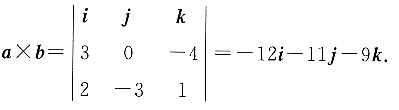
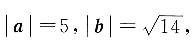
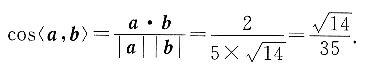
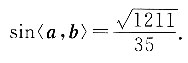
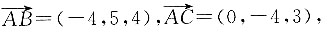
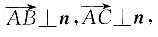

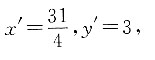
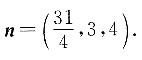
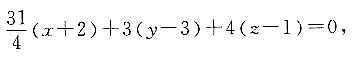
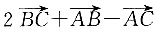 的模;
的模;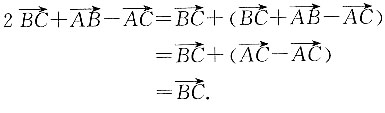
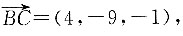
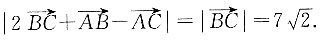
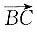 为其所在直线l的方向向量,且直线过C(-1,-3,1),
为其所在直线l的方向向量,且直线过C(-1,-3,1),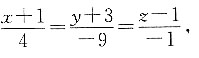

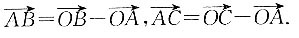
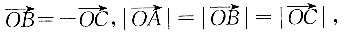
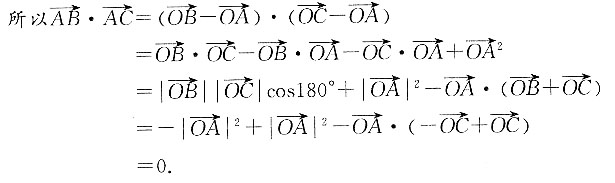
 即∠BAC=90°.
即∠BAC=90°.
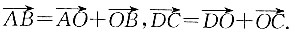
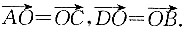
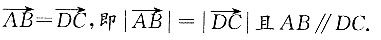

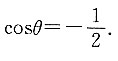
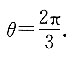
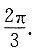
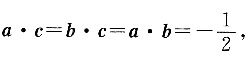
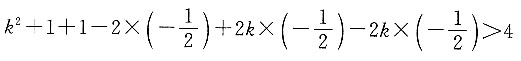

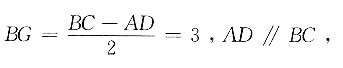
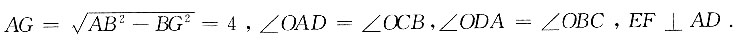
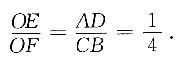
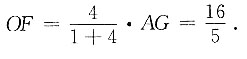
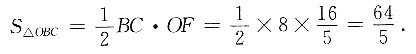

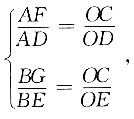 又因为AF=BG,即
又因为AF=BG,即