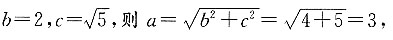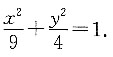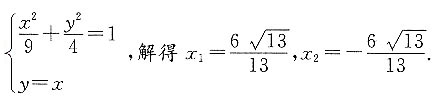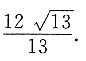一、单项选择题2. 同底的三棱锥和三棱柱的体积比为2:1,则它们的高之比为______.
A B C D
C
[解析]
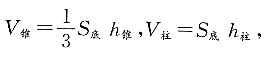
已知V
锥:V
柱=2:1,S
底相等,因此h
锥:h
柱=b:1.
3. 如图所示,一只蚂蚁在底面半径为1cm,高为
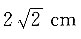
的圆锥侧面运动,自A点出发运动一圈后又回到A点的最短距离为______.

A.2π
B.2
C.
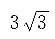
D.3
A B C D
C
[解析] 沿PA将圆锥展开,如图所示,A点到A'点的最短距离为AA'.半径为1cm,高为
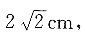
则母线长为3cm,
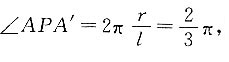
所以
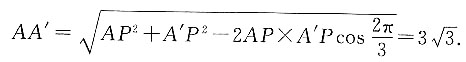
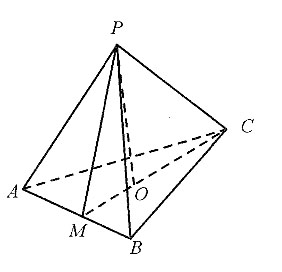
6. P—ABC为正三棱锥,其高是底面边长的
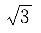
倍,则底面面积与△PMC面积的比值为______.
A.
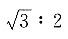
B.
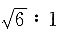
C.1:3
D.
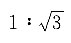
A B C D
D
[解析] 设底面边长为a,M为AB中点,根据正三角形性质可知,
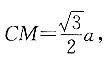
因为高OP是底面边长的
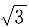
倍,即
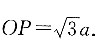
所以
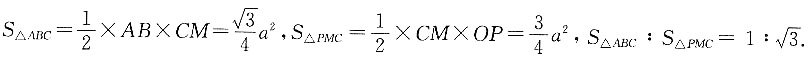
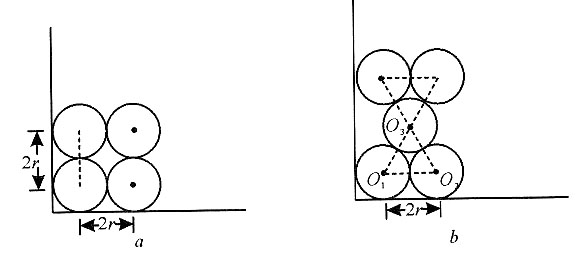
7. 一个带盖的长方体容器,底面是边长为10cm的正方形,高为11cm,最多可放入______个半径为1cm的圆球.(要求盖子正好盖住容器,厚度忽略不计)
A B C D
D
[解析] 根据题意要尽可能多地往容器中放球,有两种摆放方式,一种如图a所示,一层可以放
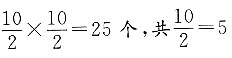
层,恰好能盖住盖子,这时可放入125个;一种如图b所示,第一层有25个,第二层有(5-1)×(5-1)=16个,第三层有25个,第四层有16个……以此类推,O
1O
2O
3为边长为2cm的等边三角形,高为
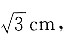
两层球时的高度为
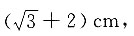
三层时高度为
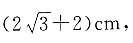
四层时高度为
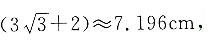
五层时高度为
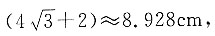
六层时高度为
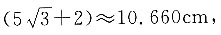
七层时高度为
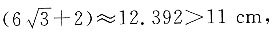
所以只放能六层,此时若第六层放25个球,总高度为

故这时可放入25+16+25+16+25+25=132个.所以第二种情况放入的球多,最多能放入132个.
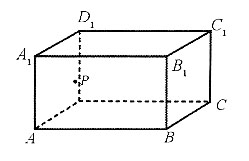
8. 在长方体ABCD—A
1B
1C
1D
1内,点P是面ABB
1A
1上的动点,且点P到直线BC的距离等于点P到直线AA
1的距离.已知AA
1=BC=2,AB=3,则P点在面ABB
1A
1上的轨迹为______.
A.
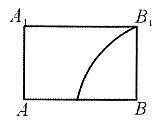
B.
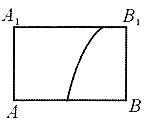
C.
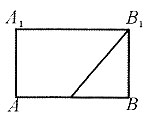
D.

A B C D
B
[解析] 在长方体ABCD—A
1B
1C
1D
1中,因为BC⊥面ABB
1A
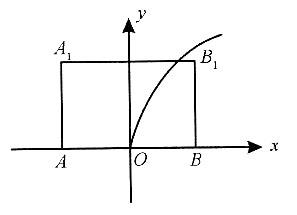
1,所以点P到BC的距离即为点P到点B的距离,动点到定点与定直线的距离相等,符合抛物线的性质,以AB的中点为原点,AB为x轴,如图所示,
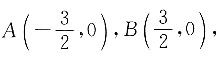
P点的轨迹在y
2=6x(y≥0)上,当y=2时,
所以轨迹应为B项.
9. 如图所示的四面体A—BCD,AD⊥面BCD,BD⊥CD,BD=1,CD=2,AD=2,则该四面体的内切球的半径为______.
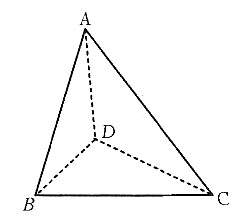
A.
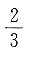
B.
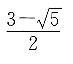
C.
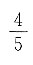
D.
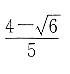
A B C D
D
[解析] 四面体内切球半径r即内切球的圆心O到面的距离,利用体积法得V
A—BCD=V
O—ABC+V
O—ACD+V
O—ABD+V
O—BCD,根据已知得
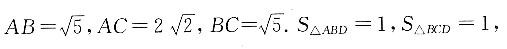
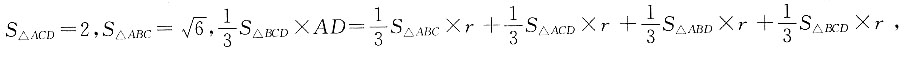
故
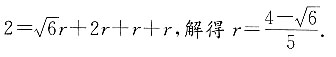
10. 在三棱柱ABC—A
1B
1C
1中,D、E、F分别是A
1C
1、BB
1、CC
1的中点,则与面ABB
1A
1平行且在面DEF内的直线有______.
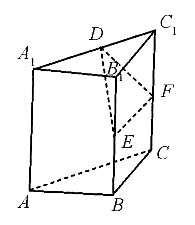
A B C D
D
[解析] 作距面ABB
1A
1距离为d的平行面α,因为面ABB
1A
1与面DEF相交,所以α与面DEF相交,交线为l,又因为α∥面ABB
1A
1,
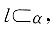
所以l∥面ABB
1A
1且
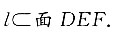
α有无数种可能,所以在面DEF中,有无数条直线与l平行,所以答案选D.
11. 若直线l
1:(a-1)y+(a+1)x=3与直线l
2:3ay=ax+1互相垂直,则a的值为______.
A B C D
C
[解析] 由题,直线l
1与直线l
2互相垂直,因此a≠-1,直线l
1的斜率为
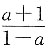
,直线l
2的斜率为
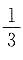
,因为两条直线相互垂直时,斜率的乘积为-1,所以
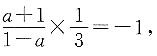
解得a=2.
12. 下列命题中,正确的一项是______.
A.已知点A(x
1,y
1),点B(x
2,y
2),则过这两点的直线的斜率

B.已知直线方程为y-y
1=k(x-x
1),则此直线斜率为k,且过点(-x
1,-y
1)
C.已知直线方程为
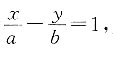
则直线与x轴、y轴的截距分别为a、b
D.与直线Ax+By+C=0平行的直线可表示为Ax+By+C
1=0
A B C D
D
[解析] 选项A中,若x
1=x
2,则直线的斜率不存在,因此不能用
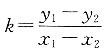
表示斜率;选项B中,直线经过的点应为(x
1,y
1),因为k值不确定,所以(-x
1,-y
1)不一定在直线上;选项C中,直线方程可化为
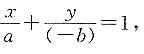
与x轴、y轴的截距分别为a、-b;选项D表述正确.
13. 过点A(1,-2)和B(3,0)且圆心在直线
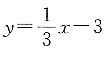
上的圆的方程是______.
- A.(x-3)2+y2=8
- B.(x-3)2+(y+2)2=4
- C.(x-3)2+(y+2)2=8
- D.(x-3)2+(y-2)2=4
A B C D
B
[解析] 设这个圆的圆心坐标为(a,b),则点A、B到圆心的距离相等,且圆心在直线
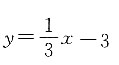
上,故有
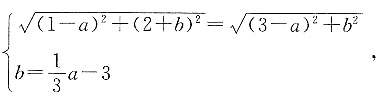
化简得
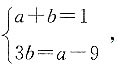
解得
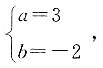
则圆心坐标为(3,-2),半径
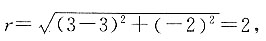
圆的方程为(x-3)
2+(y+2)
2=4,故应选择B.
14. 若方程
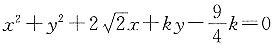
表示的方程是圆,则k的取值范围为______.
- A.k>-1或k<-8
- B.k>-1
- C.-8<k<-1
- D.k<-8
A B C D
A
[解析] 圆的一般方程为x
2+y
2+Dx+Ey+F=0,需满足条件D
2+E
2-4F>0,结合题干方程即为

化简为k
2+9k+8>0,解得k>-1或k<-8.
16. 已知椭圆的方程为3x
2+k
2y
2=15k
2,且其焦点在y轴上,那么k的取值范围是______.
A.
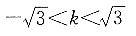
B.-1<k<1
C.
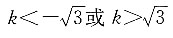
D.
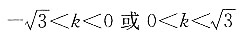
A B C D
D
[解析] 由题,椭圆方程可化简为
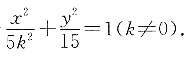
因为焦点在y轴上,所以5k
2<15,解得
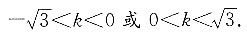
17. 若双曲线
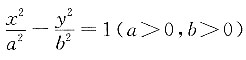
的渐近线与抛物线
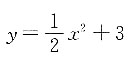
相切,则双曲线的离心率为______.
A.
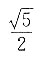
B.
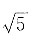
C.
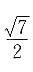
D.
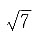
A B C D
D
[解析] 双曲线
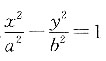
的渐近线方程为
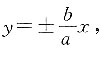
因为渐近线方程和抛物线方程都关于y轴对称,则选择其中一条进行讨论.联立方程
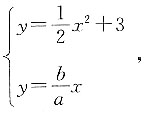
则可得
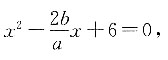
因为抛物线与双曲线的渐近线相切,则此方程只有一个解,即
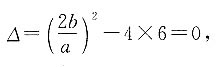
解得
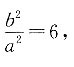
所以c
2=a
2+b
2=7a
2,故离心率
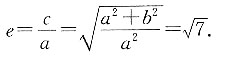
18. 设椭圆的两个焦点分别为F
1、F
2,若椭圆上有一点P,△F
1PF
2为等边三角形,则椭圆的离心率为______.
A.
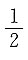
B.
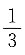
C.1
D.
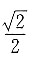
A B C D
A
[解析] 已知△F
1PF
2为等边三角形,则PF
1=PF
2,故点P在线段F
1F
2的垂直平分线上,即点P为椭圆短轴的端点,故
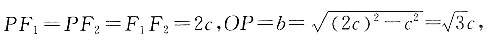
椭圆的离心率
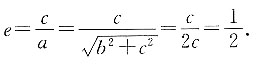
19. 已知二元一次方程3x
2-7x+2=0的两根分别为椭圆和双曲线的离心率e
1、e
2,则3(e
2-e
1)=______.
A.
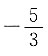
B.5
C.7
D.
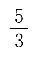
A B C D
B
[解析] 求解3x
2-7x+2=0的两根为
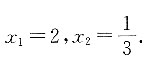
因为椭圆的离心率0<e
1<1,双曲线的离心率e
2>1,故
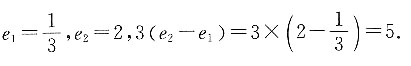
20. 在空间直角坐标系内有三点A、B、C,其中C为AB连线上的一点,O为原点,已知A点坐标为(x
1,y
1,z
1),B点坐标为(x
2,y
2,z
2),若
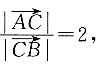
则C点坐标为______.
A.
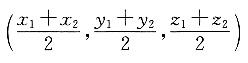
B.
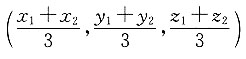
C.
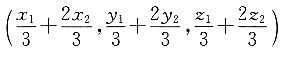
D.
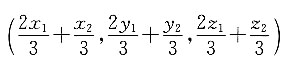
A B C D
C
[解析] 根据空间向量的定比分点公式,有
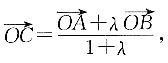
已知λ=2,A(x
1,y
1,z
1),B(x
2,y
2,z
2),则
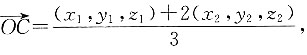
化简可得,C点坐标为
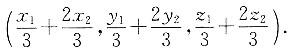
二、填空题1. 下列观点正确的是______.
①若直线a平行于平面α,则直线a平行于平面α内的所有直线;
②a是平面α外的一条直线,若a平行于平面α内的直线b,则a∥α;
③若a∥α,b∥α,则a//b;
④若平面α内有两条直线分别平行于平面β,则α∥β;
⑤直线a、b分别垂直于平面α,则a∥b.
②⑤
[解析] 直线a与平面α平行,α内存在无数的直线与a平行,但不是全部,①错;平行于同一平面的两条直线位置关系有三种情况——平行、异面、相交,③错;如果平面α内的两条直线a、b相互平行且平行于平面β,则α、β有可能相交,④错.
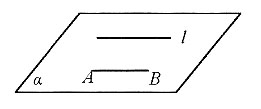
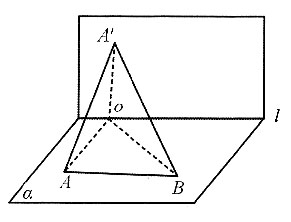
2. 如图所示,A、B两点在面α上,且AB∥l,已知A点到l的距离为2,AB=2.现以l为轴,将A点旋转120°后得到A'点,则A'B=______.
4
[解析] 根据要求作图,过A点作AO⊥l,连接A'O、BO、A'B,∠AOA'=120°,A'O=AO=2,A'O⊥l,所以l⊥面AOA'.又因为AB∥l,所以AB⊥面AOA',所以AB上AA'.AA'
2=OA
2+OA'
2-2×OA×OA'cos120°=12,
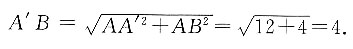
3. 分别以Rt△ABC的两条直角边为轴,旋转360°后,得到两种圆锥,体积比为4:1,则它们的侧面积比为______.
4:1
[解析] 设Rt△ABC的两直角边长分别为a、b,根据题意旋转后得到的圆锥体积分别为
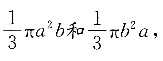
两圆锥体母线长均为
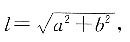
因为

则a:b=4:1.两圆锥的侧面积S
侧1=πal,S
侧2=πbl.所以侧面积的比为a:b=4:1.
4. 某正八棱柱的三视图如图所示,则它的体积为______.
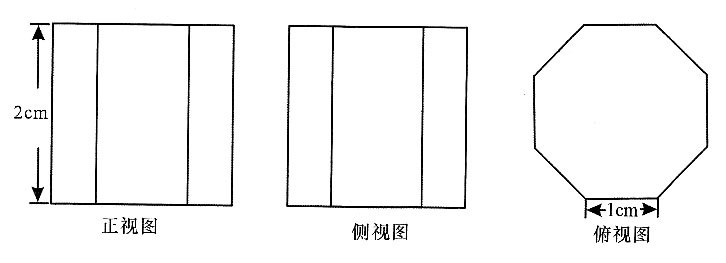
[解析] 该正八棱柱可以看成长方体切去四个直三棱柱.根据题意可知,底边正八边形的边长为1cm,正八棱柱的高为2cm,则可求得底面正方形的边长为
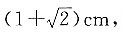
体积为
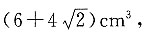
一个直三棱柱的体积为
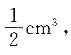
则正八棱柱的体积为
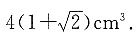
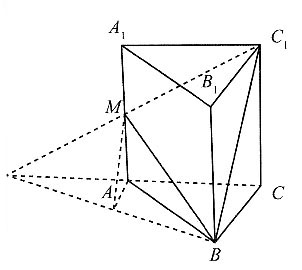
5. 如图所示的直三棱柱,AB⊥BC,MA=MA
1=AB=BC=1,则面MBC
1与底面ABC的夹角的正切值为______.
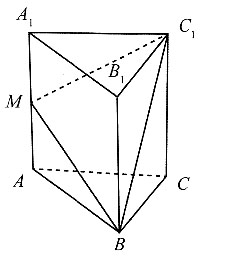
[解析] 延长C
1M与CA,交于N点,连接BN,则BN即为面MBC
1与底面ABC的的交线.过A点作AD⊥DN,连接MD.因为三棱柱为直三棱柱,所以MA⊥面ABC,又
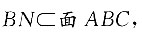
所以MA⊥BN,又MA∩AD=A,所以BN⊥面MDA,即BN⊥MD,所以∠MDA即面ABC与面MBC
1的二面角,根据余弦定理求得.
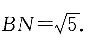
因为
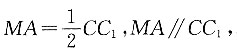
所以
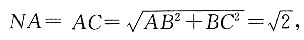
因为AB=BC=1,BC⊥AB,所以
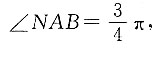
在
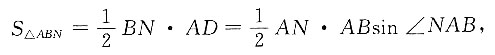
即
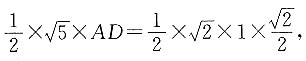
求得
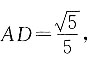
以两平面夹角的正切值
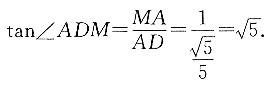
6. 已知平面直角坐标系中有点A(2,1),过A点且与两坐标轴都相切的圆的方程为______.
(x-1)2+(y-1)2=1或(x-5)2+(x-5)2=25
[解析] 已知圆经过点A(2,1),且与两坐标轴相切,则可知此圆一定在第一象限,圆心到两坐标轴的距离均为其半径长.设其半径为r,则圆的方程为(x-r)2+(y-r)2=r2.将点A的坐标代入,可得(2-r)2+(1-r)2=r2,化简可得r2-6r+5=0,解得r=1或5.故圆的方程为(x-1)2+(y-1)2=1或(x-5)2+(x-5)2=25.
7. 半径分别为5、2的两个圆外切,则外公切线的长度是______.
[解析] 已知半径分别为r
1、r
2的两圆,其外公切线的长度的平方等于圆心距的平方与半径差的平方之差.题干中两圆外切,则圆心距为两圆半径之和,所以外公切线的长度为
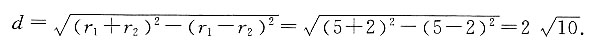
8. 已知直线l
1上有点A(2,1)和点B(4,n),直线l
2的方程为y=4x+3,若直线l
1和直线l
2垂直,则n=______.
[解析] 两直线垂直,则它们的斜率之积为-1,已知直线l
2的斜率为4,直线l
1过A、B两点,故
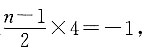
解得
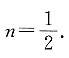
9. 已知椭圆的中心在原点上,焦点在x轴上,且已知长轴长为
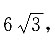
离心率为
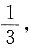
则这个椭圆的方程为______.
[解析] 已知椭圆焦点在x轴上,设椭圆方程为
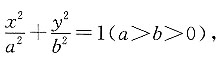
已知
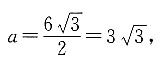
a
2=27,
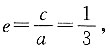
故
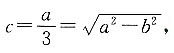
解得
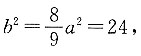
故椭圆的方程是
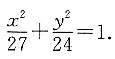
10. 已知过两直线l
1:2x-3y+3=0和
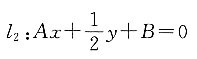
交点的直线系方程为:4x-2y+1=0,则A+B=______.
0
[解析] 依据题意可知,过两直线的交点的直线系方程为:(A
1x+B
1y+C
1)+λ(A
2x+B
2y+C
2)=0,整理得(A
1+λA
2)x+(B
1+λB
2)y+(C
1+λC
2)=0.因为
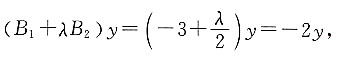
所以
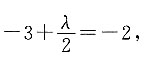
解得λ=2,所以2+2A=4,解得A=1,3+2B=1,解得B=-1,所以A+B=0.
三、解答题1. 已知四棱锥P—ABCD底面为梯形,PD⊥底面ABCD,CD//AB,AD⊥AB,AB=2PD=2CD=AD=2.求二面角P—BC—D的正切值.
延长BC,过D作DE垂直于BC并交于E点,∠PED即为所求二面角.
取AB中点F,连接CF.
因为AF//CD且AF=CD=1,所以AD//CF且AD=CF=2.
又因为AD⊥AB,所以CF⊥AB,由此求得
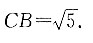
在△DEC和△CFB中,
因为∠DEC=∠CFB=90°,∠DCE+∠CDE=∠DCE+∠BCF=90°
所以∠CDE=∠BCF,
所以△DEC∽△CFB.

即二面角P—BC—D的正切值为
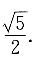
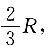 高为R的空心无盖圆柱形容器上.(容器的厚度忽略不计).
高为R的空心无盖圆柱形容器上.(容器的厚度忽略不计).
求:2. 球的顶端到容器底面的距离L;
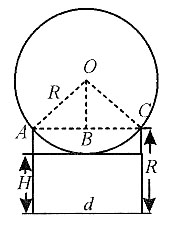
如图所示,沿圆柱的轴作切面,
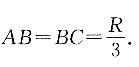
则在Rt△OBA中,
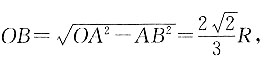
所以球的顶端到容器底面的距离
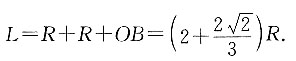
3. 向容器内注水,当水面刚好与球面相切时,水的体积.
由图可知,水面与球面相切时的高度为H,则
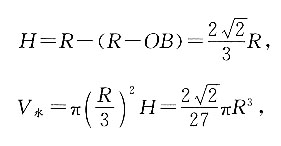
因此水面刚好与球面相切时,水的体积为
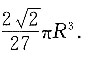
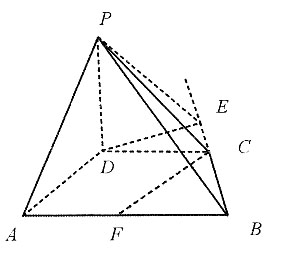
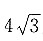 的等边三角形,E为PC中点,F在PB上,G在PD上,且
的等边三角形,E为PC中点,F在PB上,G在PD上,且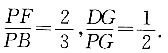
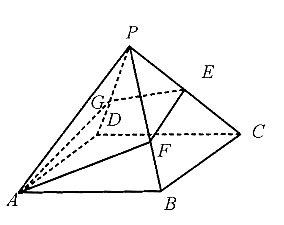
4. 证明:点A、E、F、G在同一平面;
连接AC、BD、AE、FG,AC∩BD=0,
以O为原点,AC为x轴,BD为y轴,OP为z轴,建立空间直角坐标系,
设AE∩OP=M,FG∩OP=N.
在正四棱锥P—ABCD中,
因为侧面是面积为
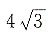
的等边三角形,设边长为a,
即
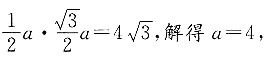
所以

则各点的坐标为:
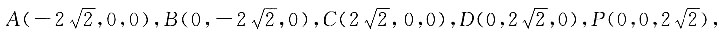
又因为,
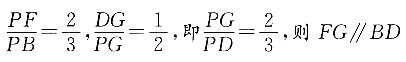
所以

因为
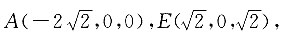
所以M的坐标为
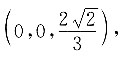
即点M和点N重合,所以AE与GF交于一点.
又因为经过两条相交直线有且只有一个平面,
所以AE与GF在平面AFEG内,即点A、E、F、G在同一平面.
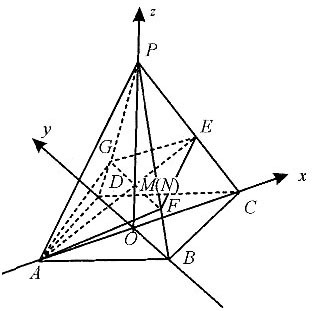
5. 求平面AFEG与底面夹角的余弦值.
AE∩GF=M,平面AFEG与底面的交线为l,
因为

所以FG//l//BD.
在正四棱锥P—ABCD中,
因为
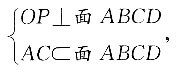
所以OP⊥AC,
又因为
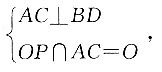
所以BD⊥面PAC,推出BD⊥AE,
则AE⊥l,AC⊥l,AE∩AC=A,
因此∠EAC即为所求二面角,
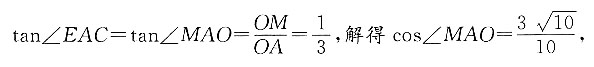
即平面AFEG与底面夹角的余弦值为
 沿对角线BD将梯形ABCD折叠成如图(b)所示的四面体.当△ABD的面积是△CBD在底面投影面积的2倍时,
沿对角线BD将梯形ABCD折叠成如图(b)所示的四面体.当△ABD的面积是△CBD在底面投影面积的2倍时,
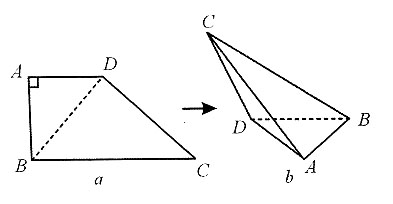
求:6. 二面角A—BD—C的余弦值;
如图所示,C点在底面的投影为O,E、F为AB、AD的中点,过O作OM⊥BD,连接CM,则∠CMO即为所求二面角,
△OBD即是△CBD在底面的投影,△ABD与△CBD同底.
因为S
△ABD=2S
△OBD,
所以O在EF的延长线上,则
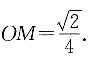
又因为
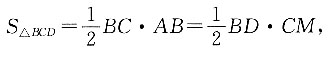
所以
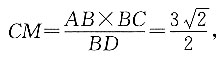
所以
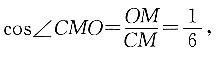
即二面角A—BD—C的余弦值为

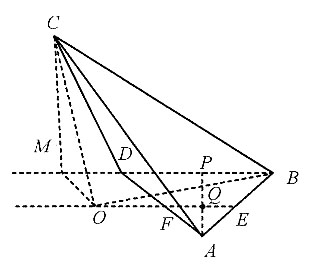
7. AC的长度.
因为OC⊥底面ABC,△COA为直角三角形,
根据(1)可知

过A作AP⊥BD交EF于Q,
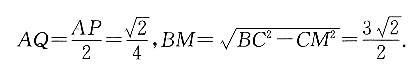
又因为
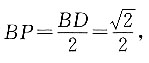
所以
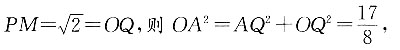
则
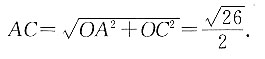
8. 判断表面积相同的正方体和长方体的体积大小关系,并证明.
当正方体和长方体的表面积相同时,正方体的体积大于长方体的体积.
设长方体的三边分别为a、b、c,正方体的边长为l,
因为表面积相同,所以2ab+2ac+2bc=6l
2,即ab+ac+bc=3l
2.
根据均值定理可知
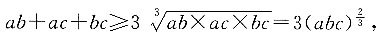
当且仅当a=b=c时取等号,
即
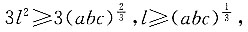
又因为V
正=l
3,V
长=abc,所以l
3≥abc,即V
正≥V
长,
当且仅当a=b=c时取等号,此时长方体即为正方体,所以不能取等号.
所以当正方体和长方体的表面积相同时,正方体的体积大于长方体的体积.
9. 已知⊙C与直线y-2x-2=0和直线y-2x+4=0都相切,且圆心在直线
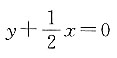
上,则求⊙C的方程.
由图⊙C与两直线均相切,且从方程式可知,这两条直线平行.又因为直线y-2x-2=0与直线
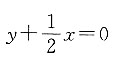
的斜率的乘积为-1,故这两条直线垂直,即圆心所在直线与圆的两条切线均垂直,由此可知,两切线所截得的部分即为圆的直径,图象如下:
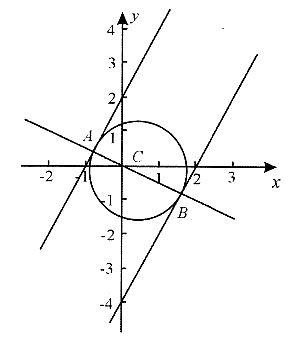
故AB为圆的直径,联立方程
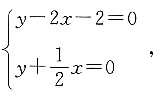
解得点A的坐标为
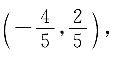
同理,联立
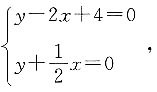
解得点B的坐标为
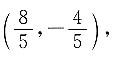
点C为A、B的中点,则其坐标为
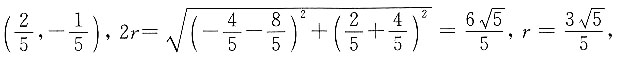
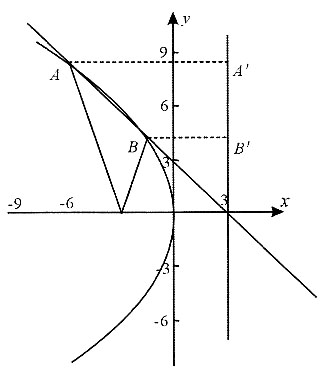
故⊙C的方程为
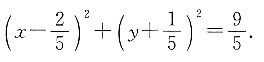
10. 已知直线y=k(x-3)(k<0)与抛物线y
2=-12x相交于A、B两点,F为抛物线的焦点,若|FA|=2|FB|,求直线的方程.
由题意k<0可知直线与抛物线的交点在第二象限.
因为抛物线的方程为y
2=-12x,
则焦点为(-3,0),准线方程为x=3.
如图所示,设B点横坐标为m(m<0),A点横坐标为n(n<0),则B点纵坐标为k(m-3).抛物线上一点到焦点的距离等于这点到准线的距离,且|FA|=2|FB|,
则有3-n=2(3-m),即n=2m-3,所以A点横坐标为2m-3,纵坐标为2k(m-3),故有

解得
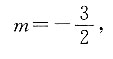
将m的值代入方程组中,
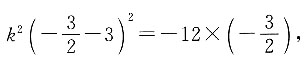
解得
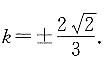
已知k<0,所以
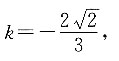
所以直线的方程为
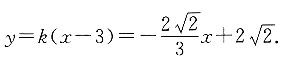
11. 求过点A(2,2,-3)且通过直线
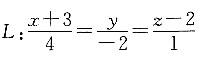
的平面方程.
因为直线的方程为

则直线的方向向量为s=(4,-2,1),直线必定经过点,B(-3,0,2),则
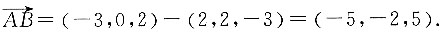
在直线上选择一点C(1,-2,3),则
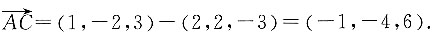
设平面的一个法向量为n
0=(m,n,p),则
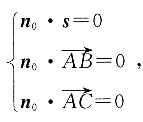
将坐标代入可得:
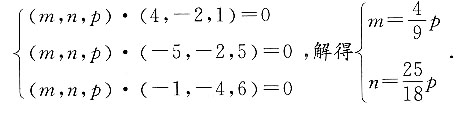
令p=18,则平面的一个法向量为(8,25,18),由此可得,平面的点法式方程为
8(x-2)+25(y-2)+18(z+3)=0,即为8x+25y+18z-18=0.
12. 已知x、y满足约束条件
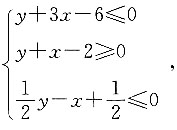
若z=y-x,求z的最大值.
标记三条直线分别为
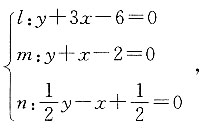
根据所给的不等式组可画出图形(如图),则阴影部分为符合条件的x、y的取值范围.

已知z=y-x,可化为y=x+z,z为直线y=x+z在y轴的截距.直线y=x+z斜率为正,则使z最大的点在阴影部分的最高点,即为直线l和直线n的交点q.联立直线l和直线n的方程可得:
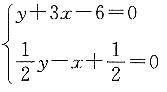
,解得

,此时
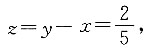
即z的最大值为
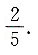
13. 在平面直角坐标系中,一椭圆以原点为中心,且短轴长为4,右焦点坐标为

若有一经过原点的直线,与x轴正方向的夹角为45°,这条直线与椭圆交于两点,求两点到y轴的距离之和.
已知椭圆
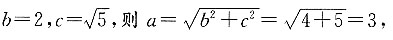
所以椭圆的方程为
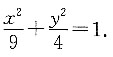
因为直线与x轴正方向的夹角为45°,
所以直线斜率k=tan45°=1,
又因为直线经过原点,故直线方程为:y=x.
由题意可知,联立方程:
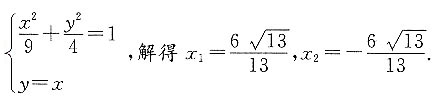
所以这两点到y轴的距离之和为
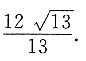
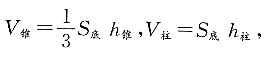 已知V锥:V柱=2:1,S底相等,因此h锥:h柱=b:1.
已知V锥:V柱=2:1,S底相等,因此h锥:h柱=b:1.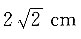 的圆锥侧面运动,自A点出发运动一圈后又回到A点的最短距离为______.
的圆锥侧面运动,自A点出发运动一圈后又回到A点的最短距离为______.
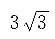
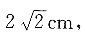 则母线长为3cm,
则母线长为3cm,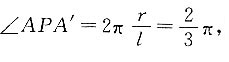 所以
所以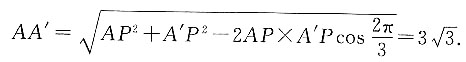

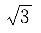 倍,则底面面积与△PMC面积的比值为______.
倍,则底面面积与△PMC面积的比值为______.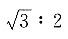
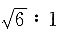
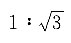
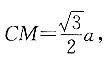 因为高OP是底面边长的
因为高OP是底面边长的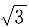 倍,即
倍,即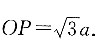 所以
所以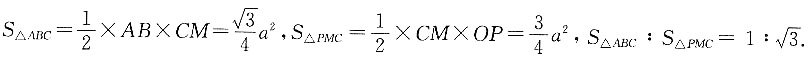

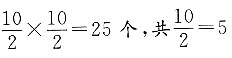 层,恰好能盖住盖子,这时可放入125个;一种如图b所示,第一层有25个,第二层有(5-1)×(5-1)=16个,第三层有25个,第四层有16个……以此类推,O1O2O3为边长为2cm的等边三角形,高为
层,恰好能盖住盖子,这时可放入125个;一种如图b所示,第一层有25个,第二层有(5-1)×(5-1)=16个,第三层有25个,第四层有16个……以此类推,O1O2O3为边长为2cm的等边三角形,高为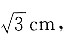 两层球时的高度为
两层球时的高度为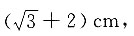 三层时高度为
三层时高度为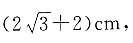 四层时高度为
四层时高度为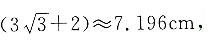 五层时高度为
五层时高度为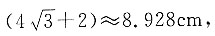 六层时高度为
六层时高度为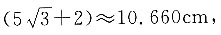 七层时高度为
七层时高度为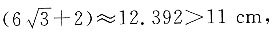 所以只放能六层,此时若第六层放25个球,总高度为
所以只放能六层,此时若第六层放25个球,总高度为 故这时可放入25+16+25+16+25+25=132个.所以第二种情况放入的球多,最多能放入132个.
故这时可放入25+16+25+16+25+25=132个.所以第二种情况放入的球多,最多能放入132个.





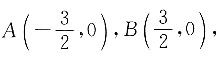 P点的轨迹在y2=6x(y≥0)上,当y=2时,
P点的轨迹在y2=6x(y≥0)上,当y=2时,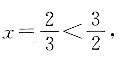 所以轨迹应为B项.
所以轨迹应为B项.

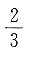
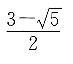
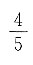
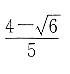
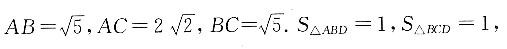
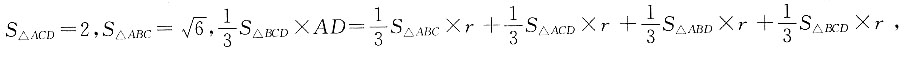 故
故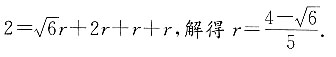

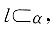 所以l∥面ABB1A1且
所以l∥面ABB1A1且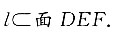 α有无数种可能,所以在面DEF中,有无数条直线与l平行,所以答案选D.
α有无数种可能,所以在面DEF中,有无数条直线与l平行,所以答案选D.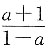 ,直线l2的斜率为
,直线l2的斜率为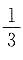 ,因为两条直线相互垂直时,斜率的乘积为-1,所以
,因为两条直线相互垂直时,斜率的乘积为-1,所以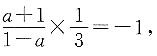 解得a=2.
解得a=2.
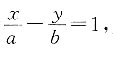 则直线与x轴、y轴的截距分别为a、b
则直线与x轴、y轴的截距分别为a、b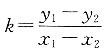 表示斜率;选项B中,直线经过的点应为(x1,y1),因为k值不确定,所以(-x1,-y1)不一定在直线上;选项C中,直线方程可化为
表示斜率;选项B中,直线经过的点应为(x1,y1),因为k值不确定,所以(-x1,-y1)不一定在直线上;选项C中,直线方程可化为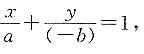 与x轴、y轴的截距分别为a、-b;选项D表述正确.
与x轴、y轴的截距分别为a、-b;选项D表述正确.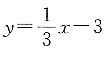 上的圆的方程是______.
上的圆的方程是______.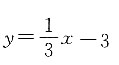 上,故有
上,故有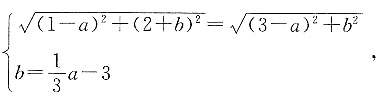 化简得
化简得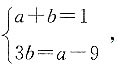 解得
解得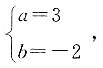 则圆心坐标为(3,-2),半径
则圆心坐标为(3,-2),半径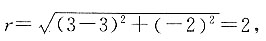 圆的方程为(x-3)2+(y+2)2=4,故应选择B.
圆的方程为(x-3)2+(y+2)2=4,故应选择B.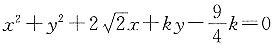 表示的方程是圆,则k的取值范围为______.
表示的方程是圆,则k的取值范围为______. 化简为k2+9k+8>0,解得k>-1或k<-8.
化简为k2+9k+8>0,解得k>-1或k<-8.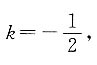 设未知直线方程为:
设未知直线方程为: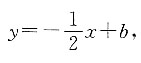 代入点(2,3),解得b=4,化简得直线方程为x+2y-8=0.
代入点(2,3),解得b=4,化简得直线方程为x+2y-8=0.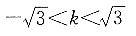
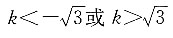
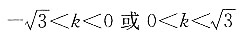
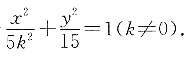 因为焦点在y轴上,所以5k2<15,解得
因为焦点在y轴上,所以5k2<15,解得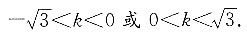
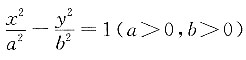 的渐近线与抛物线
的渐近线与抛物线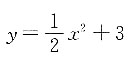 相切,则双曲线的离心率为______.
相切,则双曲线的离心率为______.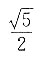
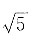
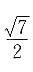
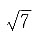
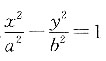 的渐近线方程为
的渐近线方程为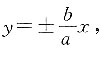 因为渐近线方程和抛物线方程都关于y轴对称,则选择其中一条进行讨论.联立方程
因为渐近线方程和抛物线方程都关于y轴对称,则选择其中一条进行讨论.联立方程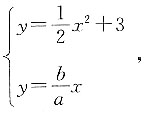 则可得
则可得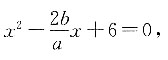 因为抛物线与双曲线的渐近线相切,则此方程只有一个解,即
因为抛物线与双曲线的渐近线相切,则此方程只有一个解,即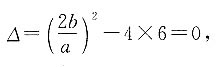 解得
解得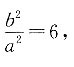 所以c2=a2+b2=7a2,故离心率
所以c2=a2+b2=7a2,故离心率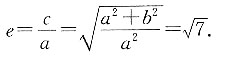
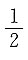
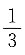
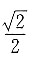
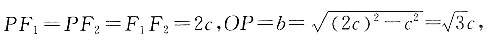 椭圆的离心率
椭圆的离心率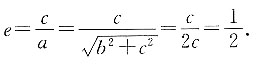
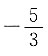
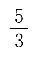
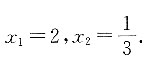 因为椭圆的离心率0<e1<1,双曲线的离心率e2>1,故
因为椭圆的离心率0<e1<1,双曲线的离心率e2>1,故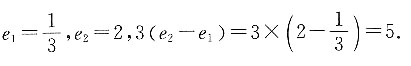
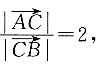 则C点坐标为______.
则C点坐标为______.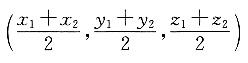
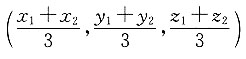
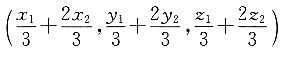
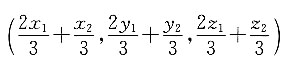
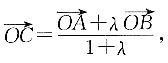 已知λ=2,A(x1,y1,z1),B(x2,y2,z2),则
已知λ=2,A(x1,y1,z1),B(x2,y2,z2),则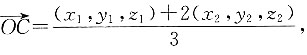 化简可得,C点坐标为
化简可得,C点坐标为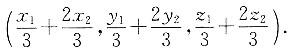

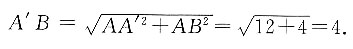

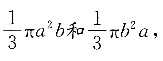 两圆锥体母线长均为
两圆锥体母线长均为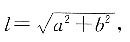 因为
因为 则a:b=4:1.两圆锥的侧面积S侧1=πal,S侧2=πbl.所以侧面积的比为a:b=4:1.
则a:b=4:1.两圆锥的侧面积S侧1=πal,S侧2=πbl.所以侧面积的比为a:b=4:1.
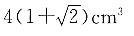
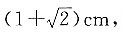 体积为
体积为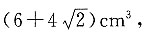 一个直三棱柱的体积为
一个直三棱柱的体积为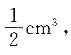 则正八棱柱的体积为
则正八棱柱的体积为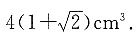

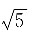
 所以MA⊥BN,又MA∩AD=A,所以BN⊥面MDA,即BN⊥MD,所以∠MDA即面ABC与面MBC1的二面角,根据余弦定理求得.
所以MA⊥BN,又MA∩AD=A,所以BN⊥面MDA,即BN⊥MD,所以∠MDA即面ABC与面MBC1的二面角,根据余弦定理求得.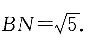 因为
因为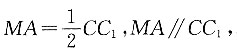 所以
所以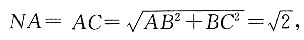 因为AB=BC=1,BC⊥AB,所以
因为AB=BC=1,BC⊥AB,所以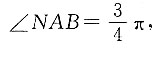 在
在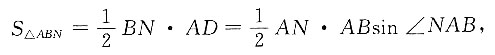 即
即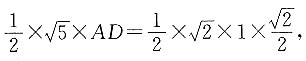 求得
求得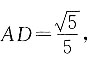 以两平面夹角的正切值
以两平面夹角的正切值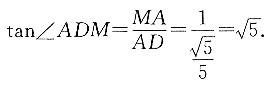

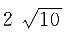
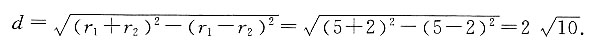
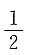
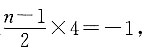 解得
解得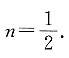
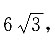 离心率为
离心率为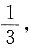 则这个椭圆的方程为______.
则这个椭圆的方程为______.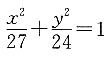
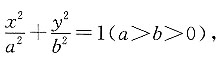 已知
已知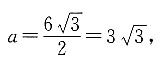 a2=27,
a2=27,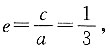 故
故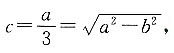 解得
解得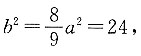 故椭圆的方程是
故椭圆的方程是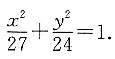
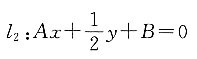 交点的直线系方程为:4x-2y+1=0,则A+B=______.
交点的直线系方程为:4x-2y+1=0,则A+B=______.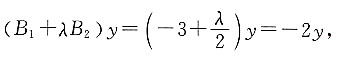 所以
所以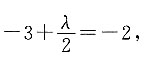 解得λ=2,所以2+2A=4,解得A=1,3+2B=1,解得B=-1,所以A+B=0.
解得λ=2,所以2+2A=4,解得A=1,3+2B=1,解得B=-1,所以A+B=0.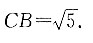

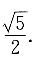

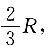 高为R的空心无盖圆柱形容器上.(容器的厚度忽略不计).
高为R的空心无盖圆柱形容器上.(容器的厚度忽略不计).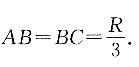
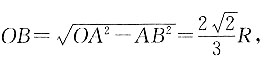
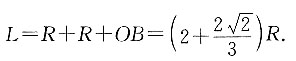

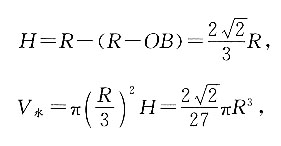
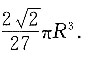
 的等边三角形,E为PC中点,F在PB上,G在PD上,且
的等边三角形,E为PC中点,F在PB上,G在PD上,且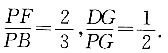

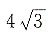 的等边三角形,设边长为a,
的等边三角形,设边长为a,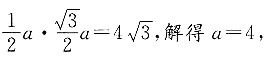

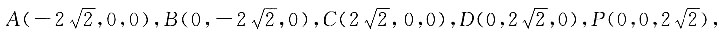
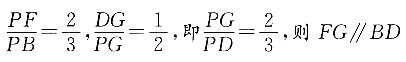

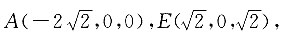
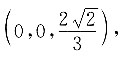


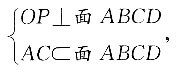
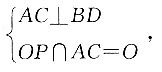
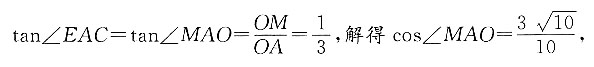
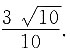
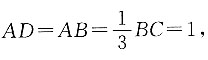 沿对角线BD将梯形ABCD折叠成如图(b)所示的四面体.当△ABD的面积是△CBD在底面投影面积的2倍时,
沿对角线BD将梯形ABCD折叠成如图(b)所示的四面体.当△ABD的面积是△CBD在底面投影面积的2倍时,
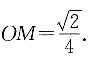
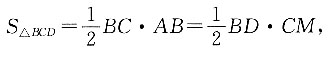
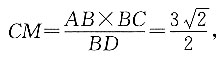
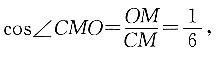 即二面角A—BD—C的余弦值为
即二面角A—BD—C的余弦值为

 过A作AP⊥BD交EF于Q,
过A作AP⊥BD交EF于Q,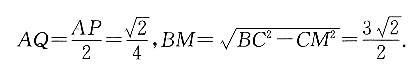
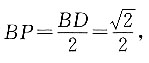
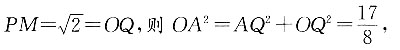
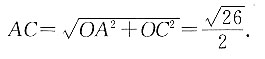
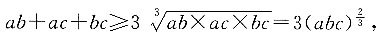 当且仅当a=b=c时取等号,
当且仅当a=b=c时取等号,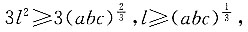
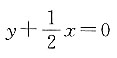 上,则求⊙C的方程.
上,则求⊙C的方程.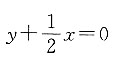 的斜率的乘积为-1,故这两条直线垂直,即圆心所在直线与圆的两条切线均垂直,由此可知,两切线所截得的部分即为圆的直径,图象如下:
的斜率的乘积为-1,故这两条直线垂直,即圆心所在直线与圆的两条切线均垂直,由此可知,两切线所截得的部分即为圆的直径,图象如下:
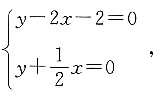 解得点A的坐标为
解得点A的坐标为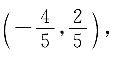 同理,联立
同理,联立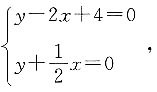 解得点B的坐标为
解得点B的坐标为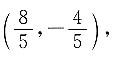 点C为A、B的中点,则其坐标为
点C为A、B的中点,则其坐标为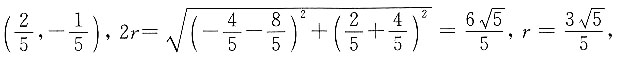 故⊙C的方程为
故⊙C的方程为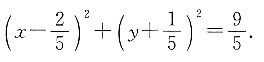
 解得
解得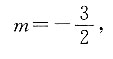
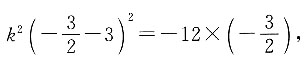
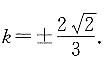
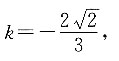
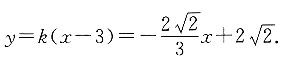

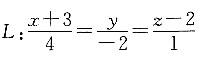 的平面方程.
的平面方程. 则直线的方向向量为s=(4,-2,1),直线必定经过点,B(-3,0,2),则
则直线的方向向量为s=(4,-2,1),直线必定经过点,B(-3,0,2),则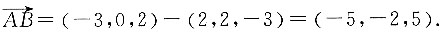 在直线上选择一点C(1,-2,3),则
在直线上选择一点C(1,-2,3),则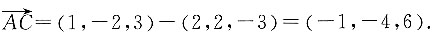
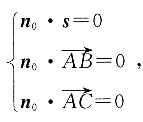 将坐标代入可得:
将坐标代入可得: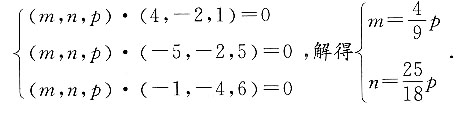
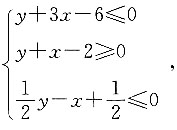 若z=y-x,求z的最大值.
若z=y-x,求z的最大值.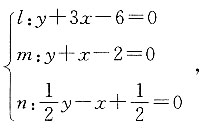 根据所给的不等式组可画出图形(如图),则阴影部分为符合条件的x、y的取值范围.
根据所给的不等式组可画出图形(如图),则阴影部分为符合条件的x、y的取值范围.
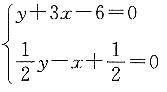 ,解得
,解得 ,此时
,此时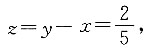 即z的最大值为
即z的最大值为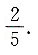
 若有一经过原点的直线,与x轴正方向的夹角为45°,这条直线与椭圆交于两点,求两点到y轴的距离之和.
若有一经过原点的直线,与x轴正方向的夹角为45°,这条直线与椭圆交于两点,求两点到y轴的距离之和.