银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
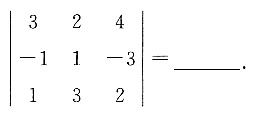
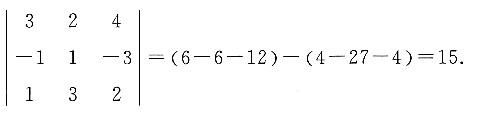
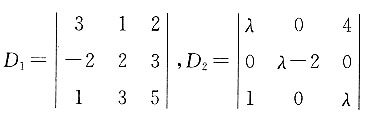，若D1=D2，则λ的值为______．
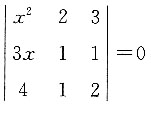，则x等于______．
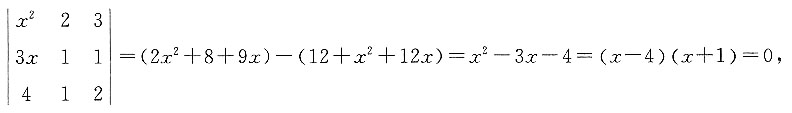所以x=4或x=-1．
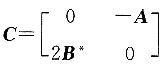，则|C|=______．
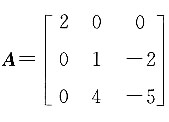合同的矩阵是______．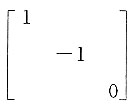
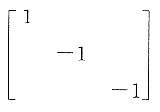
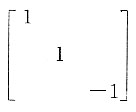
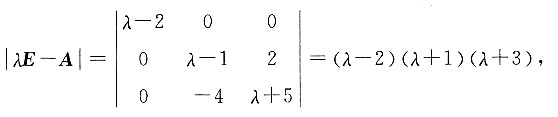所以矩阵A的特征值为-1，-3，2．即二次型的正惯性指数p=1，负惯性指数q=2．所以与矩阵A合同的矩阵中有一个正数，两个负数．
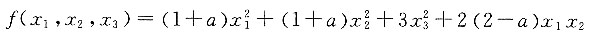的秩为2，则a的值为______．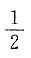
．二次型的秩为2，即矩阵的秩为2，所以
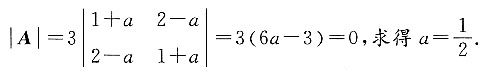
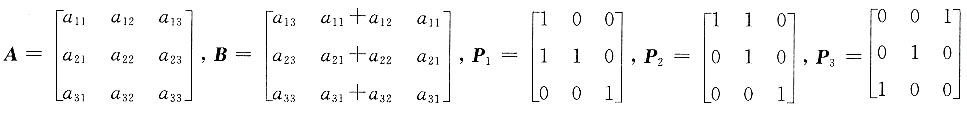，则B=______．
表示将矩阵A的第1列加至第2列，即
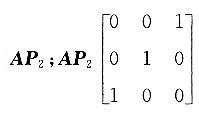表示将矩阵AP2中1，3两列互换，即AP2P3．故本题选B．
=______．
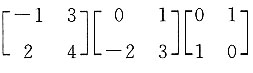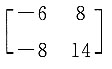
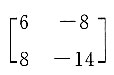
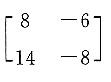
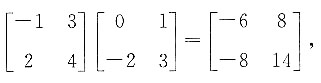
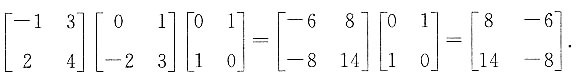
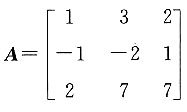，其伴随矩阵的秩为______．
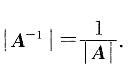因此
，如果秩r(A)=2，则α为______．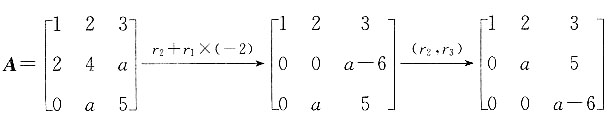
，因为秩r(A)=2，即
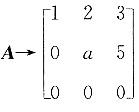，则a-6=0，求得a=6．
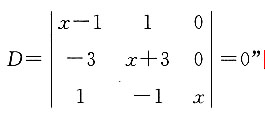的______．
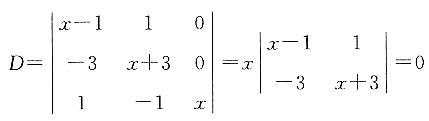，所以x=0(二重根)，x=-2．当x=0时，D=0；当D=0时，x可以为0或-2．所以x=0是行列式D=0的充分不必要条件．
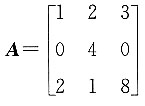，则|4A-1|=______．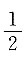
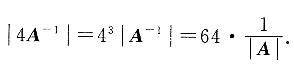又因为|A|=8，所以|4A-1|=8．
=______．
=______．
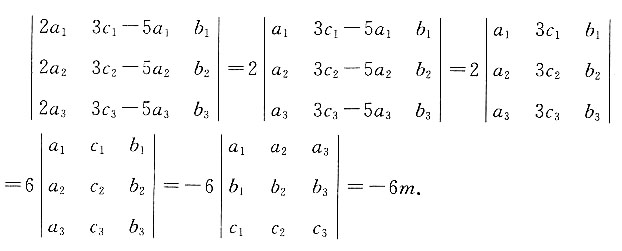
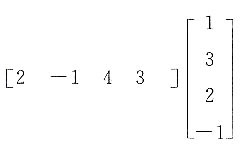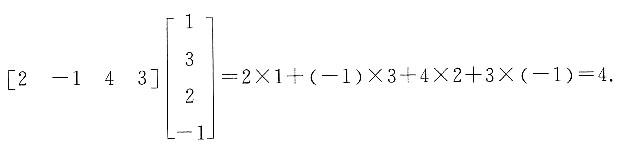
中，x3的系数是______．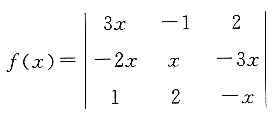
中只有3x·x·(-x)中x的指数为3，所以x3的系数为-3．
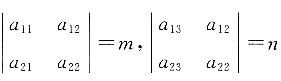，则行列式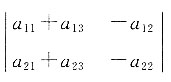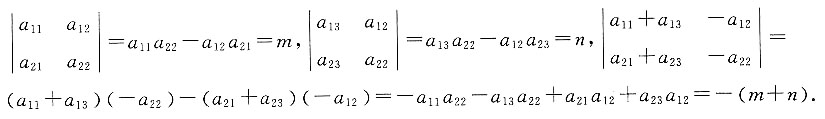
=______．
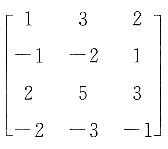的秩为______．
，所以矩阵的秩为3．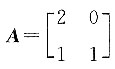
，则下列矩阵中与A可交换的矩阵B为______．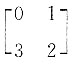
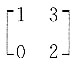
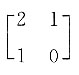
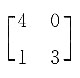
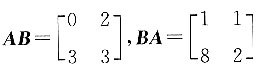，AB≠BA．将B项中的矩阵代入，
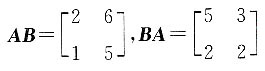，AB≠BA．将C项中的矩阵代入，
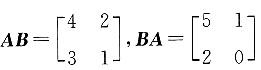，AB≠BA．将D项中的矩阵代入，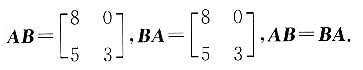
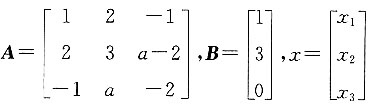．若线性方程组Ax=B无解，则a=______．
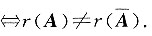对增广矩阵作初等行变换，有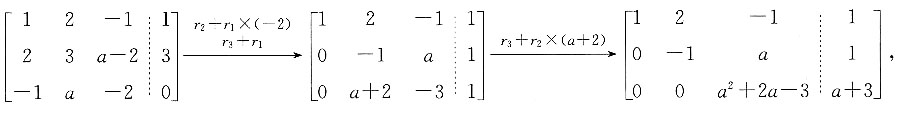
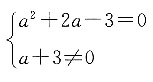，所以a=1．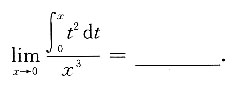
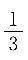
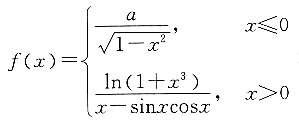在x=0处连续，则常数a=______．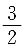
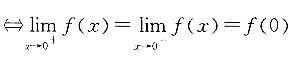．由于
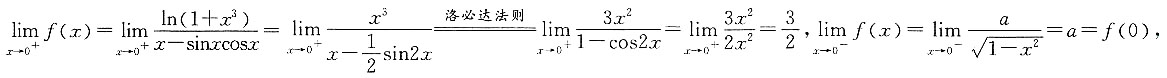因此当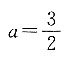
时，f(x)在x=0处连续．
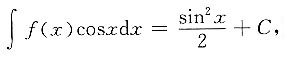又因为F(x)是f(x)的原函数，且满足F(0)=0，则F(x)=______．
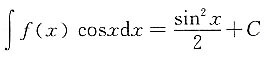两边求导得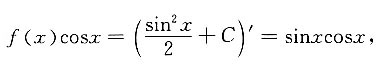
则f(x)=sinx，又因为F(0)=0，则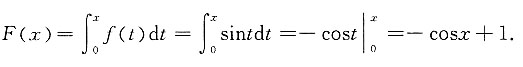
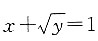与x轴、y轴围成的区域，则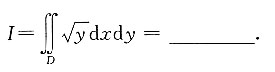
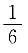
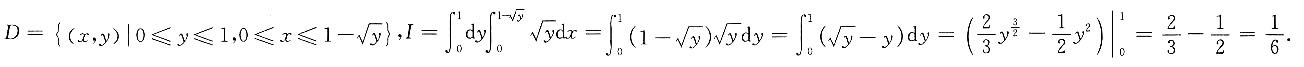
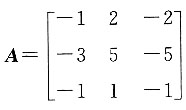若|λE-A|=0，则λ=______．
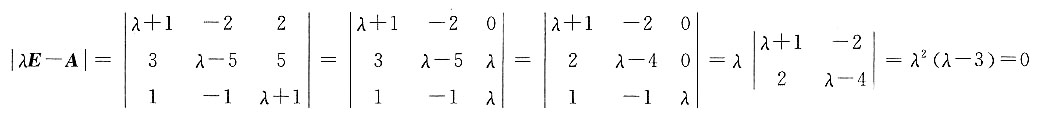，所以λ=0(二重根)或λ=3．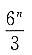
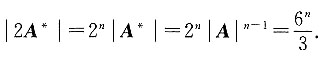
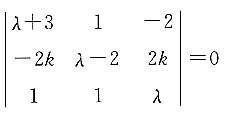，则λ=______．
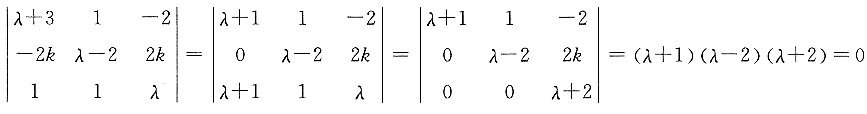，所以λ=-1或λ=±2．
，则|A|=______．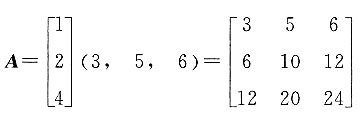
，由A中各行元素成比例可知|A|=0．
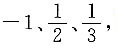进而E-6A-1的特征值为7、-2、-1，所以|E-6A-1|=7×(-2)×(-1)=14．
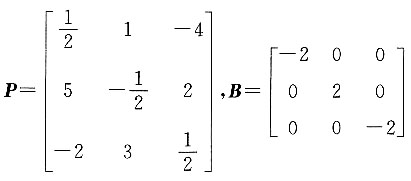，则A2012=______．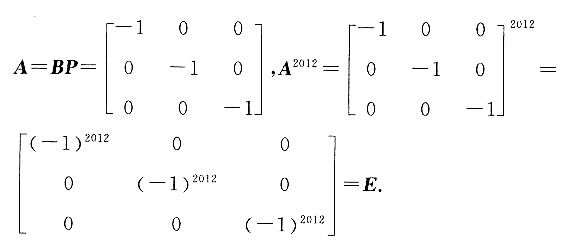
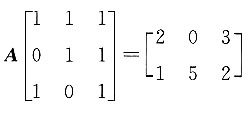，则矩阵A=______．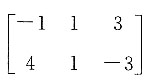
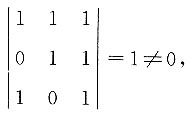则矩阵可逆，
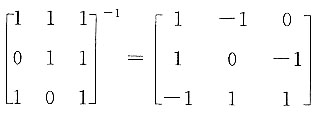．所以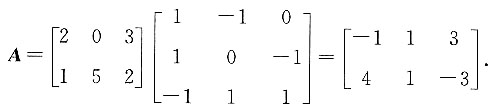
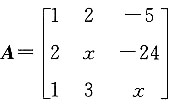不可逆，则x=______．
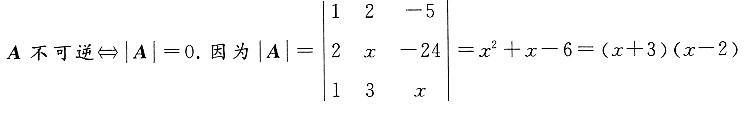，x=-3或x=2．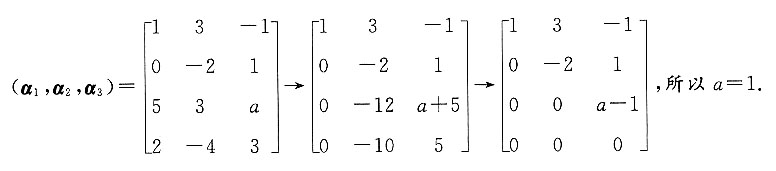
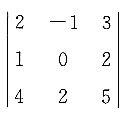的值为______．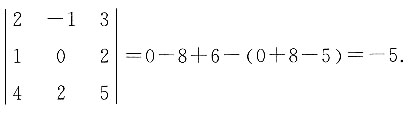
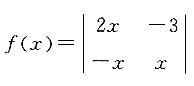非零的零点是______．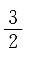
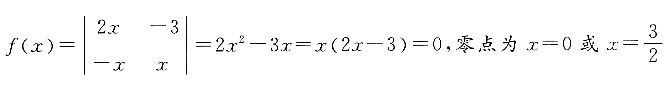，故其非零的零点为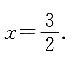
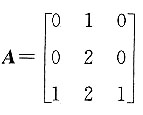，则2A1000-A1001=______．
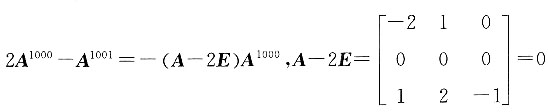，所以(A-2E)A1000=0，即2A1000-A1001=0．
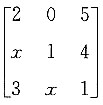的代数余子式A12=-9，则代数余子式A13=______．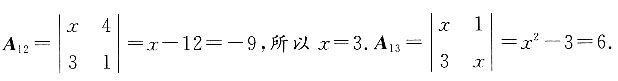
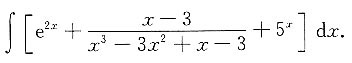
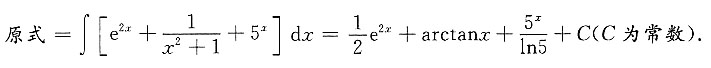
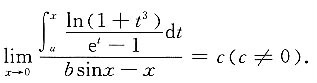
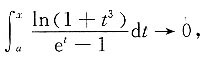故必有a=0，而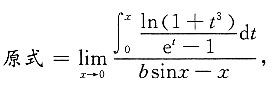
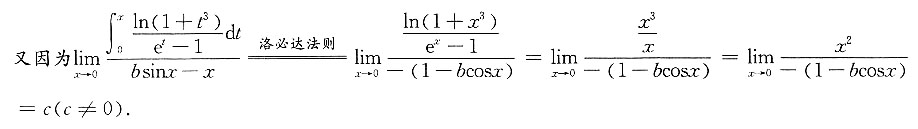
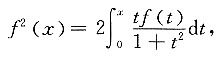求f(x)．
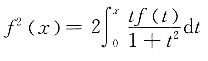两边求导可得，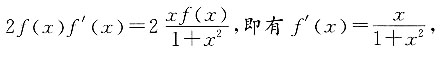
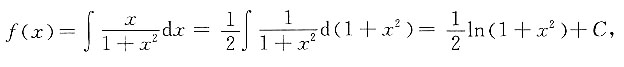
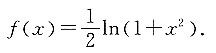
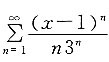的收敛半径和收敛域．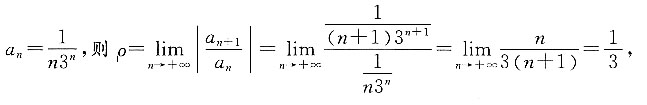
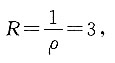
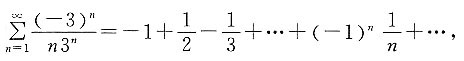
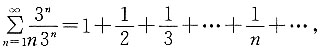此级数发散，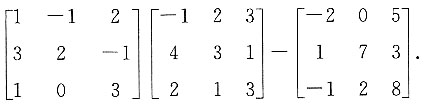
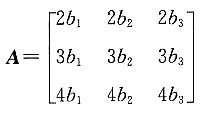，若A2=lA，则求l．
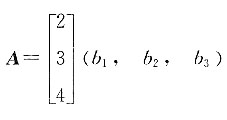，则由矩阵的乘法结合律可知：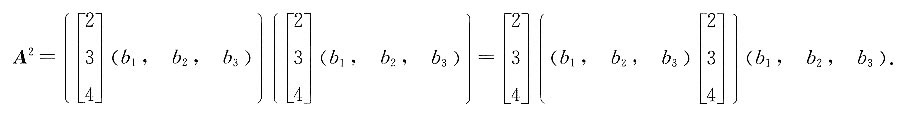
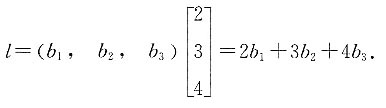
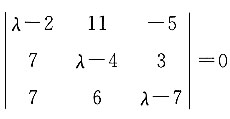，求λ的值．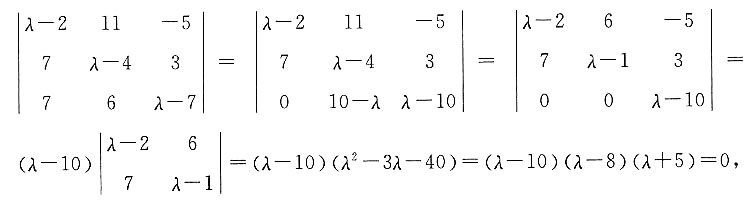
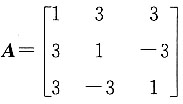的逆矩阵．
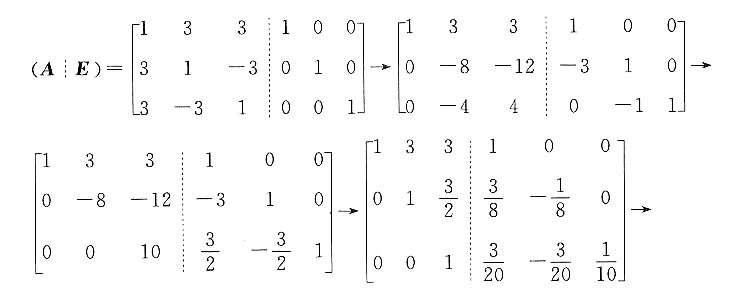
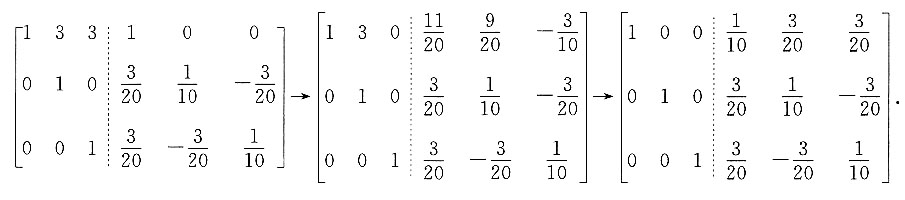
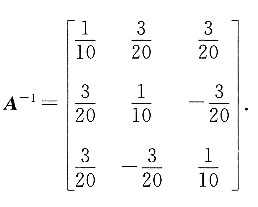
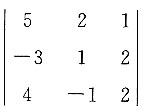的值．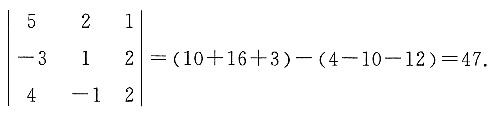
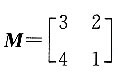的特征值及对应的特征向量．
深色：已答题 浅色：未答题