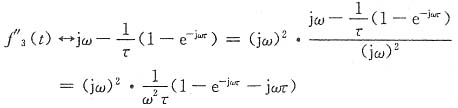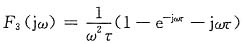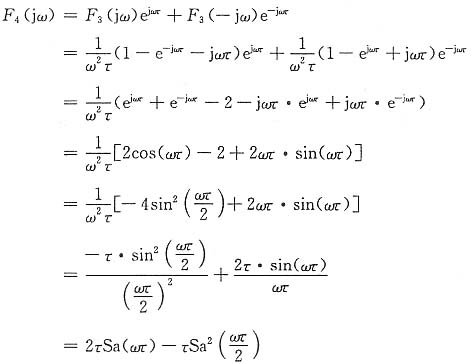计算题已知在时间区间(0,2π)上的方波信号为
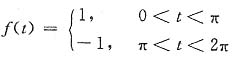
1. 如用在同一时间区间上的正弦信号来近似表示此方波信号,要求方均误差最小,写出此正弦信号的表达式;
解 设此正弦信号的表达式为csint,则在区间(0,2π)上,此正弦信号与f(t)的方均误差为
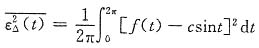
要使此方均误差最小,令
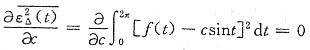
亦即
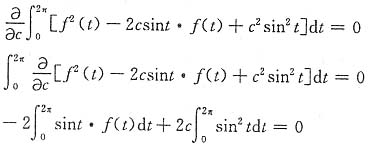
因
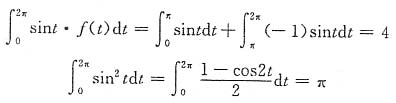
故有-8+2πc=0
从而得
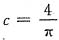
,即此正弦信号为
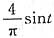
。
2. 证明此信号与同一时间区间上的余弦信号cos(nt)(n为整数)正交。
解 因
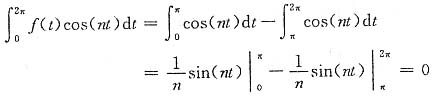
说明此方波信号与余弦信号cos(nt)(n为整数)在(0,2π)上正交。
3. 已知f
1(t)=cost+sint,f
2(t)=cost。求f
1(t)在f
2(t)上的分量系数c
12及此二信号间的相关系数ρ
12。
解 f
1(t)在f
2(t)上的分量系数
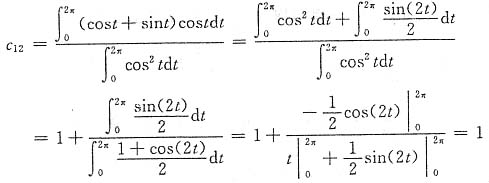
注意:若要求f
2(t)在f
1(t)上的分量系数,不妨用c
21表示,则
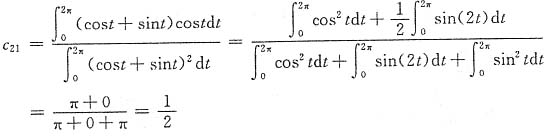
此二信号间的相关系数
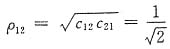
或由式
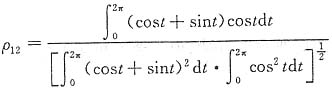
亦可计算求得
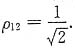
4. 证明两相互正交的信号f
1(t)与f
2(t)同时作用于单位电阻上产生的功率,等于每一信号单独作用时产生的功率之和。以f
1(t)与f
2(t)分别为下列两组函数来验证此结论。
(1)f
1(t)=cos(ωt),f
2(t)=sin(ωt)
(2)f
1(t)=cos(ωt),f
2(t)=sin(ωt+30°)
解 先简要证明结论“两相互正交的信号f
1(t)与f
2(t)同时作用于单位电阻上产生的功率等于每一信号单独作用时产生的功率之和”。假设f
1(t)与f
2(t)的周期为T,则f
1(t)与f
2(t)同时作用于单位电阻上产生的功率为
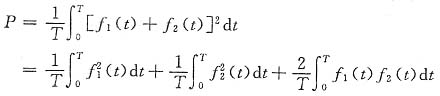
因为f
1(t)与f
2(t)正交,则
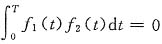
,于是
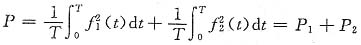
下面来验证:
(1)f
1(t)与f
2(t)的周期均为
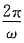
,且二者相互正交。
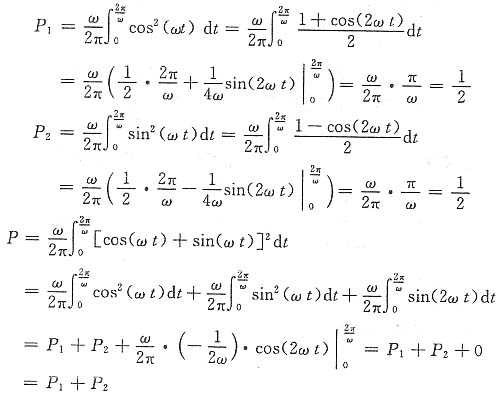
由此验证了以上结论。
(2)f
1(t)与f
2(t)的周期亦均为
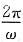
,但二者不相互正交。
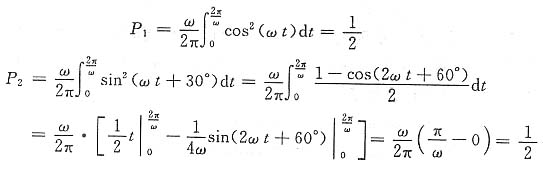
而
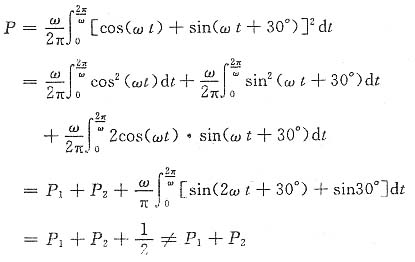
由此说明不相互正交的两信号单独作用时产生的功率之和不等于同时作用时产生的功率。
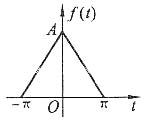
5. 将下图所示的三角形信号在时间区间(-π,π)上展开为有限项的三角傅里叶级数,使其与实际信号间的方均误差小于原信号f(t)总能量的1%。写出此有限项三角傅里叶级数的表达式。
解 题图所示三角形信号的数学表达式为
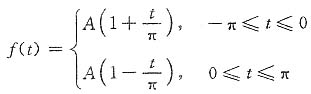
由f(t)在(-π,π)上的偶对称特性知其傅里叶系数b
n=0。又展开的时间区间为(-π,π),故T=2π,从而Ω=1。下面求系数a
0和a
n。

于是在(-π,π)上,
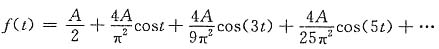
另一方面,信号的总能量
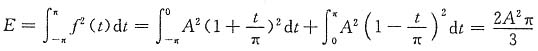
若取f(t)傅里叶级数中第一项来近似f(t),则方均误差为

而
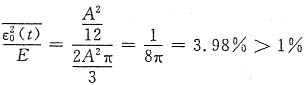
,不满足要求。
再考虑取f(t)傅里叶级数中前两项来近似f(t),则方均误差为
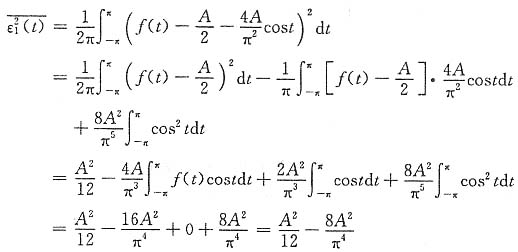
由于
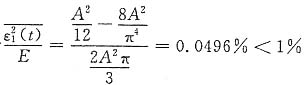
,满足要求,所以此有限项三角傅里
叶级数的表达式为
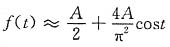
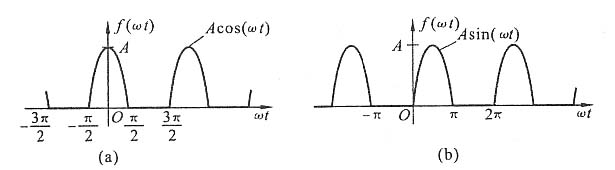
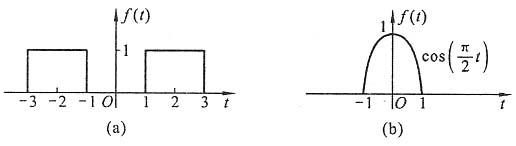
6. 求图(a)所示的周期性半波整流余弦脉冲信号及图(b)所示的周期性半波整流正弦脉冲信号的傅里叶级数展开式。绘出频谱图并作比较,说明其差别所在。
解 (a)由图(a)所示波形可得一周期内信号的表达式(由于T=2π,所以Ω=1):
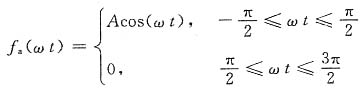
由图知函数为偶函数,故b
n=0,只需计算a
0和a
n。由题意,取ωt为变量。
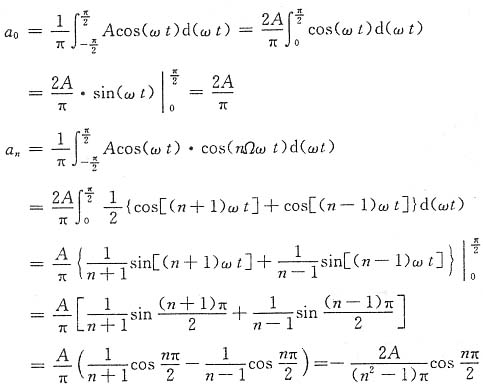
当n=1时,利用洛必达法则有
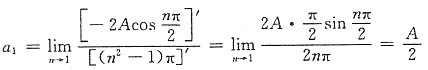
所以
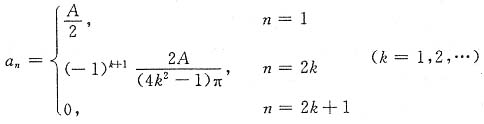
故

(b)由图(b)所示波形可知,f
b(ωt)与f
a(ωt)相比,相位滞后
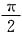
,因此
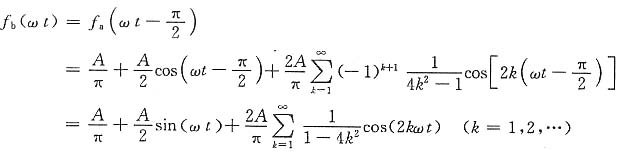
f
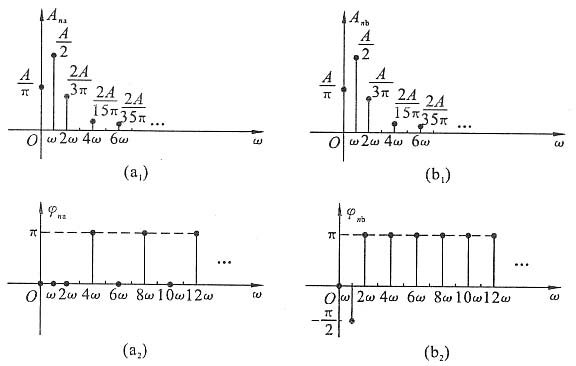
a(ωt)与f
b(ωt)的幅度频谱图分别如图(a
1)、(b
1)所示,相位频谱图分别如图(a
2)、(b
2)所示。
对比二者的频谱图可发现,f
a(ωt)与f
b(ωt)的幅度频谱相同,但相位频谱不同。由此也说明了,如果信号的波形不变,仅仅沿坐标轴产生时移,则其傅里叶展开式中,各次谐波的幅度不受影响,仅仅引起各次谐波的相移。
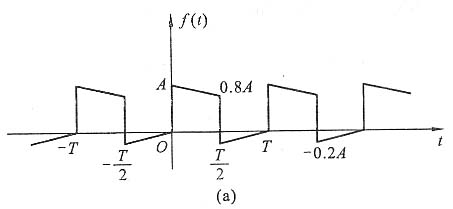
7. 利用周期性矩形脉冲与周期性三角形脉冲的傅里叶级数展开式,见教材中式(3-30)及式(3-38),求图(a)波形所示信号的傅里叶级数。
解 图(a)波形所示信号可以分解为f
1(t)与f
2(t)两个信号之差(见图(b)、(c)),即
f(t)=f
1(t)-f
2(t)
式中
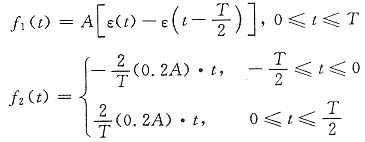
对于f
1(t),其傅里叶系数
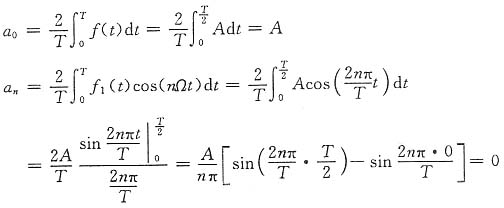
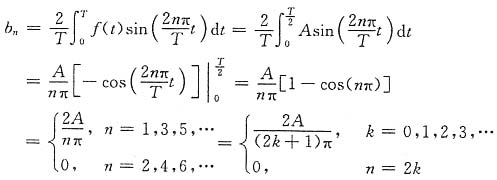
所以
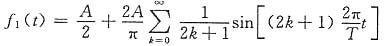
对于f
2(t),其为偶函数,故傅里叶系数b
n=0。
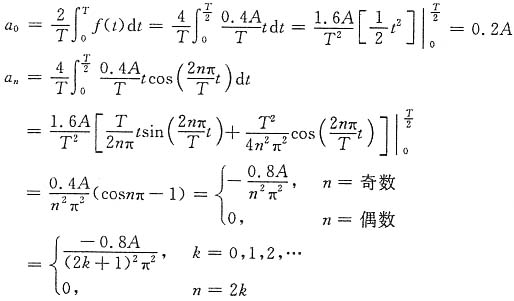
所以
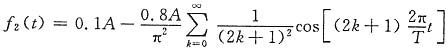
于是
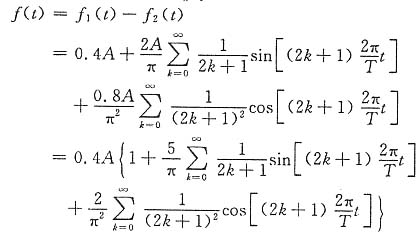
8. 试判断在
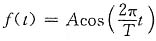
时间区间
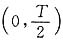
上展开的傅里叶级数是仅有余弦项,还是仅有正弦项,还是二者都有。如展开时间区间改为
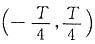
,则又如何。
解
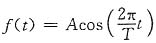
的波形如图(a)所示。
在图中,取时间区间
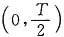
上波形进行周期延拓,得图(b)。由图(b)易知,f(t)在时间区间

上展开成一奇函数,所以f(t)在
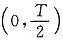
上展开的傅里叶级数仅有正弦项。
在图(a)中,取时间区间
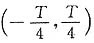
上波形进行周期延拓,得图(c)。由图(c)易知,f(t)在时间区间

上展开的傅里叶级数含有直流分量和余弦项,不含有正弦项。
9. 已知周期信号f(t)前四分之一周期的波形如图(a)所示,按下列条件绘出整个周期内的信号波形。
(1)f(t)是t的偶函数,其傅里叶级数只有偶次谐波;
(2)f(t)是t的偶函数,其傅里叶级数只有奇次谐波;
(3)f(t)是t的偶函数,其傅里叶级数同时有奇次谐坡与偶次谐波;
(4)f(t)是t的奇函数,其傅里叶级数只有偶次谐波;
(5)f(t)是t的奇函数,其傅里叶级数只有奇次谐波;
(6)f(t)是t的奇函数,其傅里叶级数同时有奇次谐波与偶次谐波。
解 若f(t)只含偶次谐波,说明f(t)是偶谐函数;若f(t)只含奇次谐波,说明f(t)是奇谐函数;若f(t)既含奇次谐波,又含偶次谐波,则f(t)既非奇谐函数,又非偶谐函数。绘图时,可先根据f(t)的奇、偶对称特性,绘出
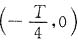
区间内的波形,再据奇谐或偶谐特性绘出另半个周期内的波形。
(1)信号波形如图(b)所示。
(2)信号波形如图(c)所示。
(3)信号波形如图(d)所示。
(4)信号波形如图(e)所示。
(5)信号波形如图(f)所示。
(6)信号波形如图(g)所示。
注意:题(3)、(6)的信号波形不仅仅只有图示一种。
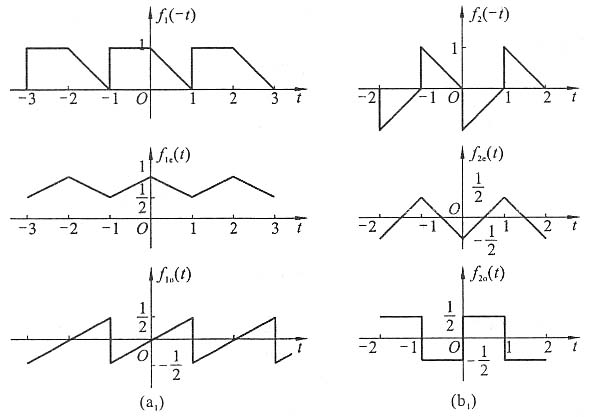
10. 试绘出图(a)、(b)所示波形信号的奇分量及偶分量的波形。
解 信号的偶分量
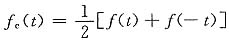
信号的奇分量
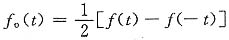
故绘偶、奇分量的波形,需先画出f(-t)的波形,再相加、减。波形如图(a
1)、(b
1)所示。
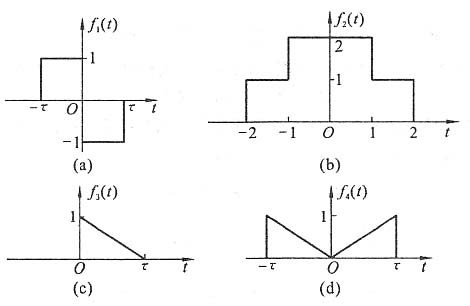
11. 利用信号的奇偶性,判断图所示各信号的傅里叶级数所包含的分量。
解 f1(t)为偶函数,且平均值为零,所以其傅里叶级数只包含余弦分量,无正弦分量和直流分量。
f2(t)为奇函数,所以其傅里叶级数只包含正弦分量,无余弦分量。
f3(t)既为偶函数,又为偶谐函数,且平均值不为零,所以其傅里叶级数含直流分量和偶次余弦分量。
f4(t)为奇谐函数,所以其傅里叶级数只含奇次谐波分量。
12. 已知f
1(t)的频谱函数为F
1(jω),f
2(t)与,f
1(t)波形有如图的关系,试用f
1(t)的频谱函数F
1(jω)来表示f
2(t)的频谱函数F
2(jω)。
解 由图可见,f
2(t)=f
1[-(t-t
0)]=f
1(t
0-t),由于
f
1(-t)
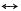
F
1(-jω)
f
1[-(t-t
0)]
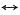
F
1(-jω)e
-jωt0 故F
2(jω)=F
1(-jω)e
-jωt0
13. 利用傅里叶变换的移频特性求图所示信号的频谱函数。
图(a)为矩形包络,可知
f
1(t)=cos(5t)·[ε(t+π)-ε(t-π)]
令G
2π(t)=ε(t+π)-ε(t-π)
则有f
1(t)=
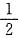
(e
j5t+e
-j5t)·G
2π(t)
由G
2π(t)

2πSa(ωπ)及频移特性
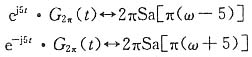
可知
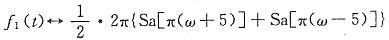
即F
1(jω)=π{Sa[π(ω+5)]+Sa[π(ω-5)]}
(2)图(b)为三角形包络,可知
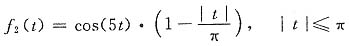
令
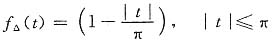
则有
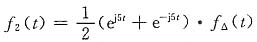
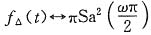
再利用频移特性可知
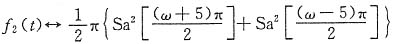
即
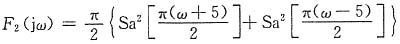
(3)图(c)所示波形为图(a)所示波形右移2π所得,故可利用时移特性有
F
3(jω)=F
1(jω)·e
-j2πω 即F
3(jω)=π{Sa[π(ω+5)]+Sa[π(ω-5)])·e
-j2πω
14. 如时间实函数f(t)的频谱函数F(jω)=R(ω)+jX(ω),试证明f(t)的偶分量的频谱函数为R(ω),奇分量的频谱函数为jX(ω)。
证明 对于实函数f(t)来说,其频谱函数的实部为偶函数,虚部为奇函数,即
R(ω)=R(-ω),X(ω)=-X(-ω)
f(t)的偶分量

其频谱函数
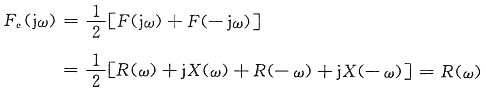
f(t)的奇分量
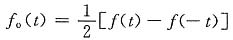
其频谱函数

15.
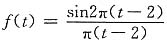
解
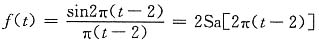
由变换对
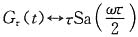
取τ=4π,于是有G
4π(t)
4πSa(2πω)
由对称特性,有4πSa(2πt)
2πG
4π(ω)
即2Sa(2πt)
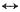
G
4π(ω)
最后利用时移特性,得
f(t)=2Sa[2π(t-2)]

F(jω)=G
4π(ω)e
-j2ω 即F(jω)=[ε(ω+2π)-ε(ω-2π)]e
-j2ω
16.
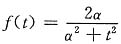
解 由变换对
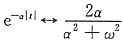
利用对称特性,有
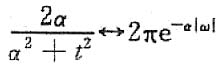
即F(jω)=2πe
-α|ω|
17.
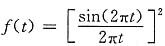
解
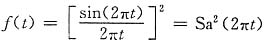
由变换对
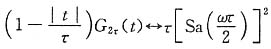
取τ=4π,于是有
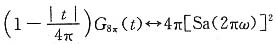
利用对称特性,有
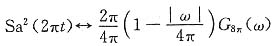
即
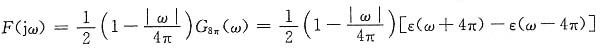
18. 求下列频谱函数对应的时间函数。
(1)F(jω)=δ(ω+ω
c)-δ(ω-ω
c)
(2)
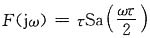
(3)
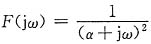
(4)
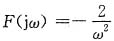
(1)
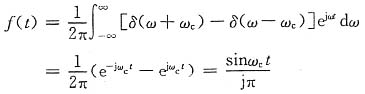
(2)
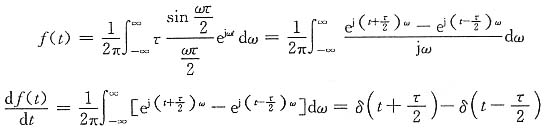
所以
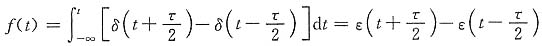
(3)由变换对
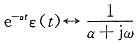
利用频域微分性质,有
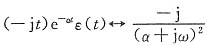
即
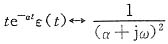
从而f(t)=te
-atε(t)
(4)因为
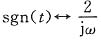
由频域微分特性,有
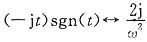
即
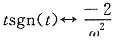
从而f(t)=tsgn(t)
注意:本题的前两个小题((1)、(2))也可利用已知的一些变换对及傅里叶变换的性质。如:
(1)由变换对1
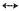
2πδ(ω),再结合频移特性,有
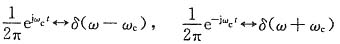
所以所求时间函数
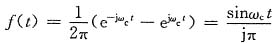
(2)
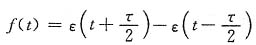
19. 试用下列特性求图所示信号的频谱函数。
(1)用延时特性与线性特性;
(2)用时域微分、积分特性。
解 图(a):
f(t)=G
2(t+2)+G
2(t-2)
(1)因为
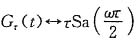
所以G
2(t)
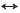
2Sa((ω)
由延时特性,有G
2(t+2)
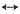
2Sa(ω)e
j2ω,G
2(t-2)
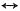
2Sa(ω)e
-j2ω 由线性特性,有
F(jω)=2Sa(ω)e
j2ω+2Sa(ω)e
-j2ω=4Sa(ω)cos(2ω)=
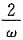
[sin(3ω)-sinω]
(2)f(t)=ε(t+3)-ε(t+1)+ε(t-1)-ε(t-3)
f'(t)=δ(t+3)-δ(t+1)+δ(t-1)-δ(t-3)

e
j3ω-e
jω+e
-jω-e
-j3ω=
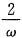
[sin(3ω)-sinω]·jω
由时域微、积分特性,有
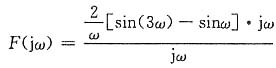
从而
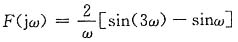
图(b):
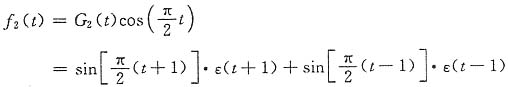
(1)先求
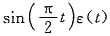
的傅里叶变换,再利用延时及线性特性。
由变换对
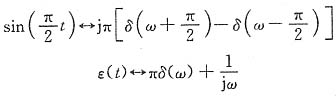
及频域卷积定理,有
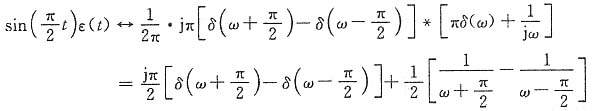
由于
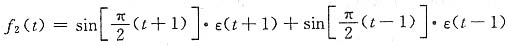
故由时移及线性特性,有
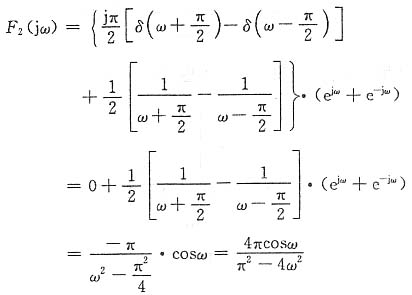
(2)对f(t)求导如下:
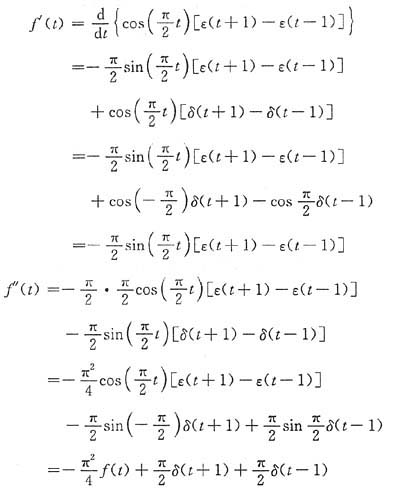
利用傅里叶变换的时域微分特性,对上式两边求FT,得
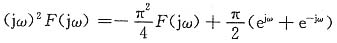
从而有
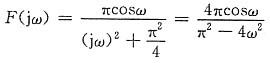
20. 试用时域微分、积分特性求图中波形信号的频谱函数。
解 (a)由图(a)可知
f(t)=t[ε(t)-ε(t-1)]+ε(t-1)
其一阶导数f'(t)=ε(t)-ε(t-1)+t[δ(t)-δ(t-1)]+δ(t-1)
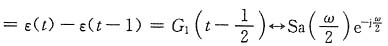
又因为
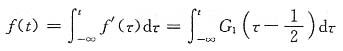
由时域积分特性知
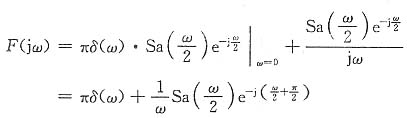
(b)由图(b)可知
f(t)=(t+2)[ε(t+2)-ε(t+1)]+[ε(t+1)-ε(t-1)]+(-t+2)[ε(t-1)-ε(t-2)]=(t+2)ε(t+2)-(t+1)ε(t+1)=(t-1)ε(t-1)+(t-2)ε(t-2)
其一阶导数
f'(t)=ε(t+2)+(t+2)δ(t+2)-ε(t+1)-(t+1)δ(t+1)-ε(t-1)-(t-1)δ(t-1)+ε(t-2)+(t-2)δ(t-2)=ε(t+2)-ε(t+1)-ε(t-1)+ε(t-2)
二阶导数f"(t)=δ(t+2)-δ(t+1)-δ(t-1)+δ(t-2)
且f"(t)
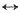
e
j2ω-e
jω-e
-jω+e
-j2ω 则由微积分特性,有
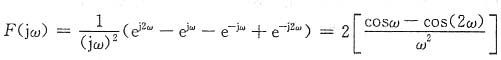
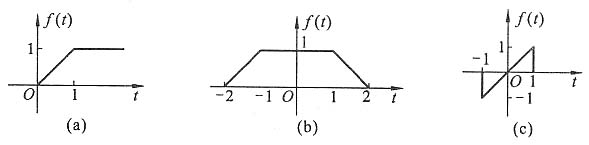
(c)由图(c)可知
f(t)=t[ε(t+1)-ε(t-1)]
其一阶导数f'(t)=ε(t+1)+tδ(t+1)-ε(t-1)-tδ(t-1)=ε(t+1)-δ(t+1)-ε(t-1)-δ(t-1)
二阶导数f"(t)=δ(t+1)-δ(t-1)-δ'(t+1)-δ'(t-1)
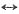
e
jω-e
-jω-jω(e
jω+e
-jω)=j2(sinω-ωcosω)
则由微积分特性,有
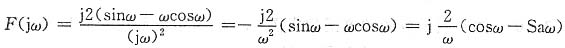
21. 利用频域卷积定理,由cos(ω
ct)的傅里叶变换及ε(t)的傅里叶变换导出cos(ω
ct)ε(t)的傅里叶变换。
解 由变换对
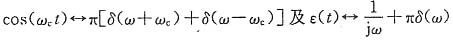
,再利用频域卷积定理,有
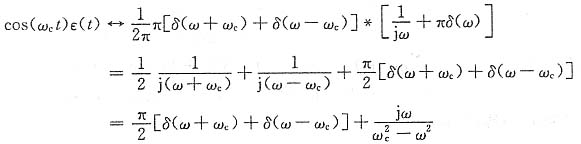
22. 由冲激函数的频谱函数求图所示波形信号的频谱函数。
由图(a)所示波形可写出
f
1(t)=ε(t+τ)-2ε(t)+ε(t-τ)
其一阶导数f'
1(t)=δ(t+τ)-2δ(t)+δ(t-τ)
且
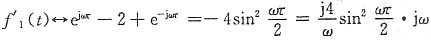
故其频谱函数
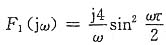
(2)由图(b)所示波形可写出
f
2(t)=ε(t+2)+ε(t+1)-ε(t-1)-ε(t-2)
其一阶导数f'
2(t)=δ(t+2)+δ(t+1)-δ(t-1)-δ(t-2)
且f
2'(t)
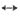
e
j2ω+e
jω-e
-jω-e
-j2ω=2j[sinω+sin(2ω)]
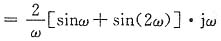
故其频谱函数
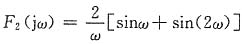
(3)由图(c)所示波形可写出
f
3(t)=-
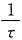
(t-τ)[ε(t)-ε(t-τ)]
其一阶导数
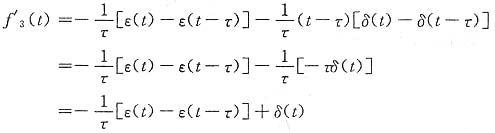
二阶导数f"
3(t)=-
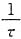
[δ(t)-δ(t-τ)]+δ'(t)
且
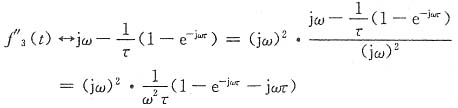
故其频谱函数
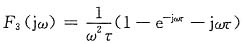
(4)观察f
4(t)的波形(见图(d)),发现其与f
3(t)有如下关系:
f
4(t)=f
3(t+τ)+f
3(-t+τ)
故可直接利用已求出的F
3(jω)及傅里叶变换的时移及反褶特性得
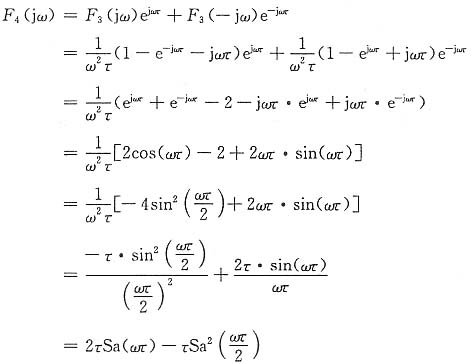
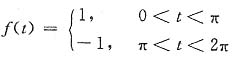
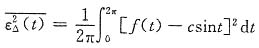
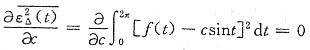
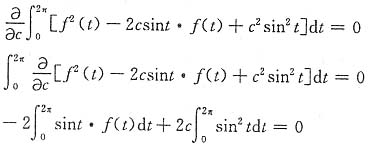
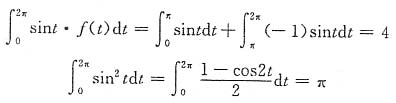
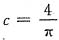 ,即此正弦信号为
,即此正弦信号为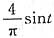 。
。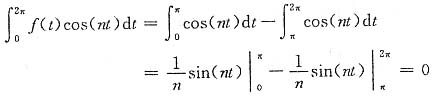
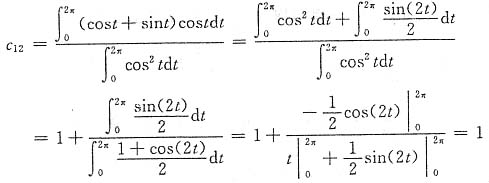
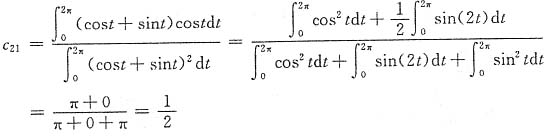
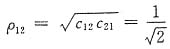
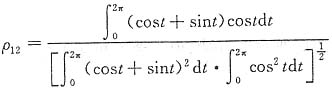 亦可计算求得
亦可计算求得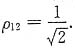
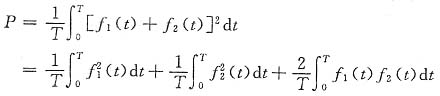
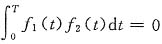 ,于是
,于是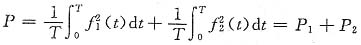
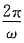 ,且二者相互正交。
,且二者相互正交。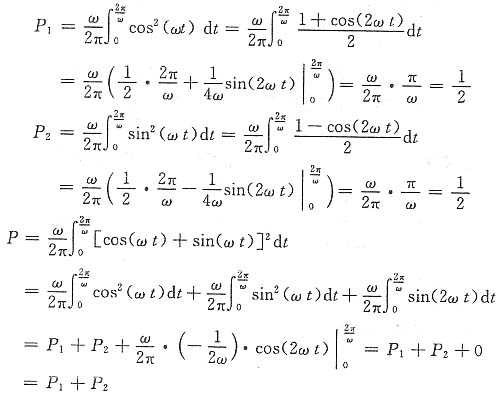
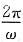 ,但二者不相互正交。
,但二者不相互正交。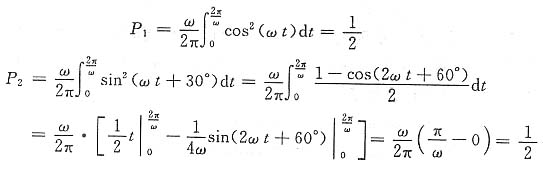
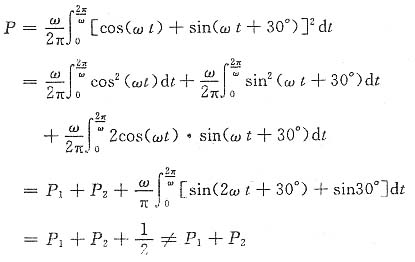
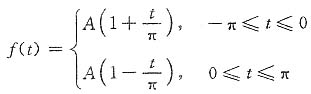

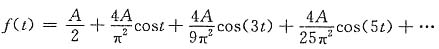 另一方面,信号的总能量
另一方面,信号的总能量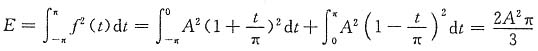

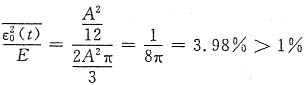 ,不满足要求。
,不满足要求。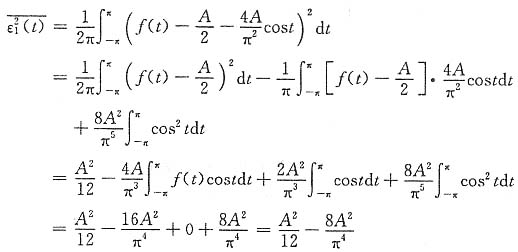
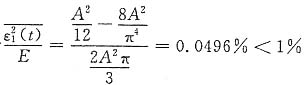 ,满足要求,所以此有限项三角傅里
,满足要求,所以此有限项三角傅里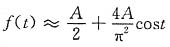
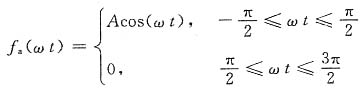
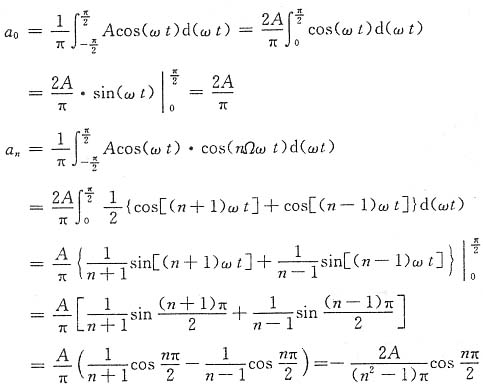
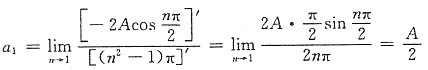
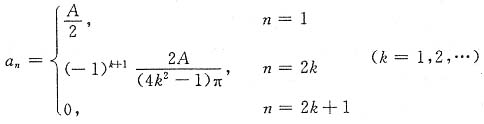

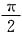 ,因此
,因此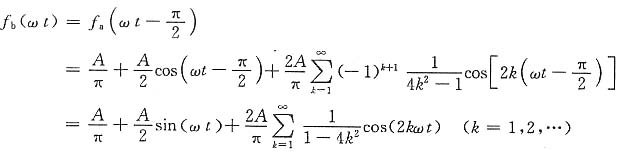

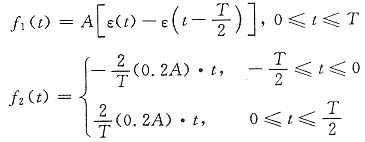
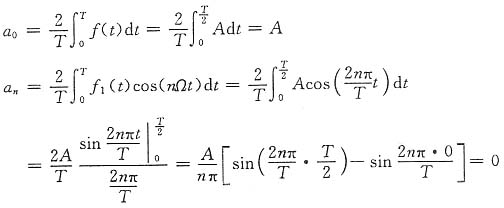
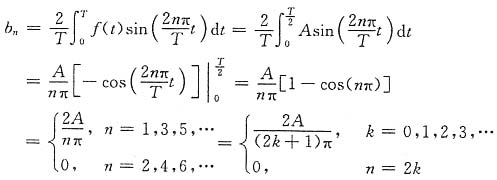
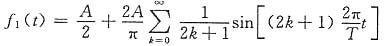
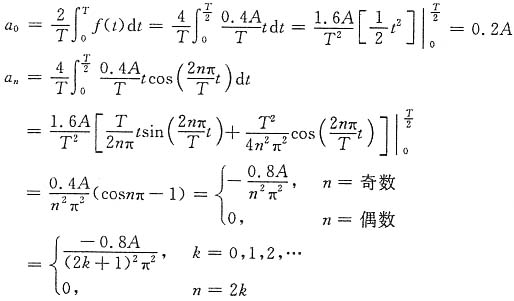
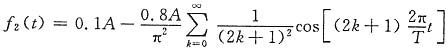
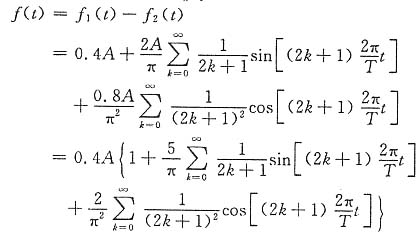
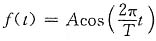 时间区间
时间区间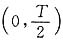 上展开的傅里叶级数是仅有余弦项,还是仅有正弦项,还是二者都有。如展开时间区间改为
上展开的傅里叶级数是仅有余弦项,还是仅有正弦项,还是二者都有。如展开时间区间改为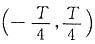 ,则又如何。
,则又如何。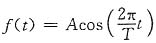 的波形如图(a)所示。
的波形如图(a)所示。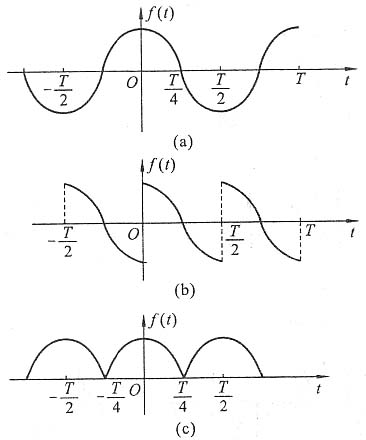
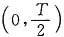 上波形进行周期延拓,得图(b)。由图(b)易知,f(t)在时间区间
上波形进行周期延拓,得图(b)。由图(b)易知,f(t)在时间区间 上展开成一奇函数,所以f(t)在
上展开成一奇函数,所以f(t)在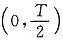 上展开的傅里叶级数仅有正弦项。
上展开的傅里叶级数仅有正弦项。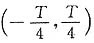 上波形进行周期延拓,得图(c)。由图(c)易知,f(t)在时间区间
上波形进行周期延拓,得图(c)。由图(c)易知,f(t)在时间区间 上展开的傅里叶级数含有直流分量和余弦项,不含有正弦项。
上展开的傅里叶级数含有直流分量和余弦项,不含有正弦项。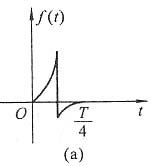
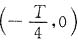 区间内的波形,再据奇谐或偶谐特性绘出另半个周期内的波形。
区间内的波形,再据奇谐或偶谐特性绘出另半个周期内的波形。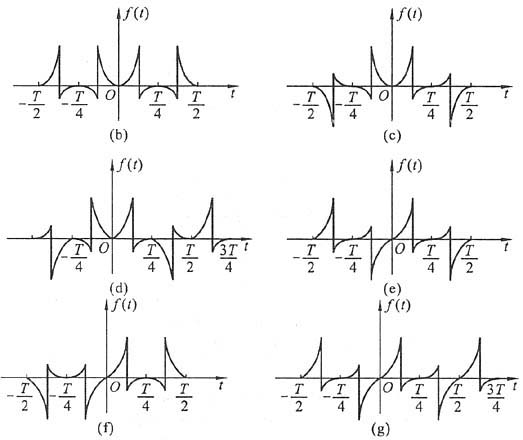
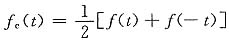
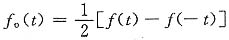

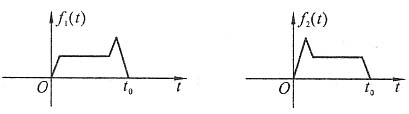
 F1(-jω)
F1(-jω) F1(-jω)e-jωt0
F1(-jω)e-jωt0
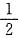 (ej5t+e-j5t)·G2π(t)
(ej5t+e-j5t)·G2π(t) 2πSa(ωπ)及频移特性
2πSa(ωπ)及频移特性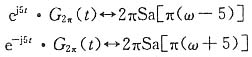
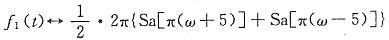
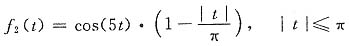
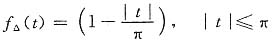
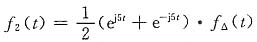
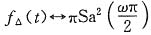
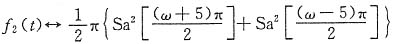
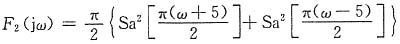

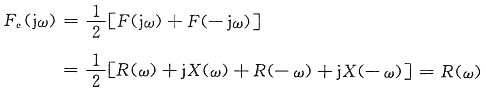
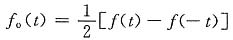

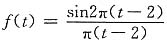
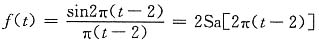
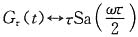
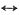 4πSa(2πω)
4πSa(2πω)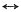 2πG4π(ω)
2πG4π(ω)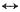 G4π(ω)
G4π(ω) F(jω)=G4π(ω)e-j2ω
F(jω)=G4π(ω)e-j2ω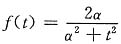
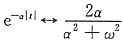
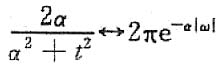
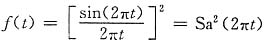
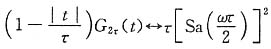
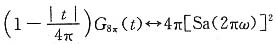
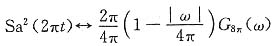
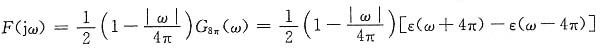
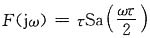
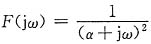
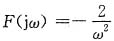
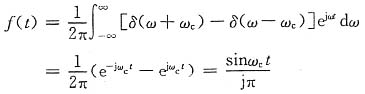
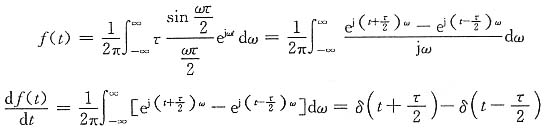
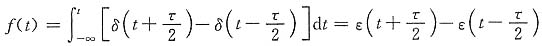
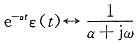
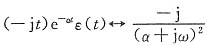
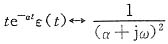
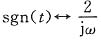
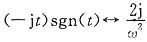
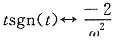
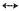 2πδ(ω),再结合频移特性,有
2πδ(ω),再结合频移特性,有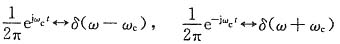
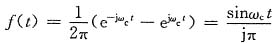
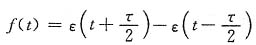
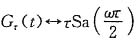
 2Sa((ω)
2Sa((ω)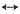 2Sa(ω)ej2ω,G2(t-2)
2Sa(ω)ej2ω,G2(t-2)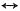 2Sa(ω)e-j2ω
2Sa(ω)e-j2ω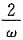 [sin(3ω)-sinω]
[sin(3ω)-sinω] ej3ω-ejω+e-jω-e-j3ω=
ej3ω-ejω+e-jω-e-j3ω=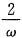 [sin(3ω)-sinω]·jω
[sin(3ω)-sinω]·jω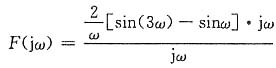
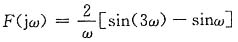
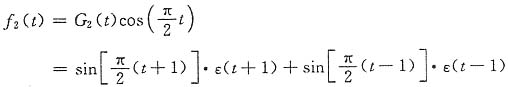
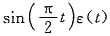 的傅里叶变换,再利用延时及线性特性。
的傅里叶变换,再利用延时及线性特性。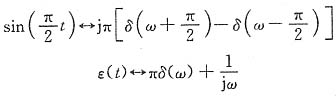
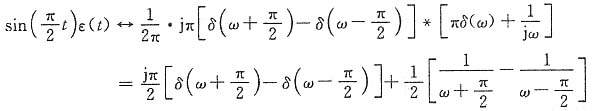
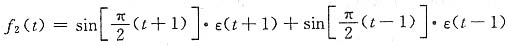

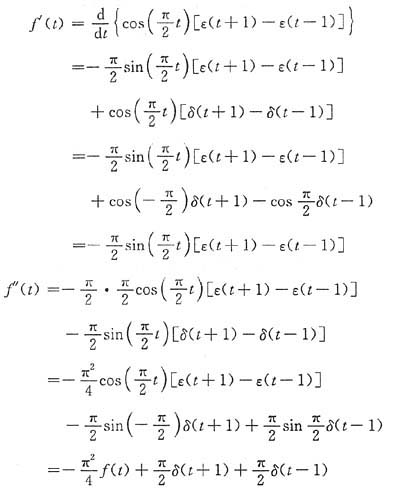
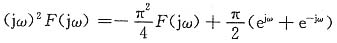
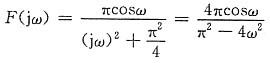
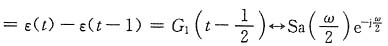
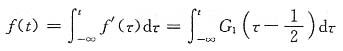
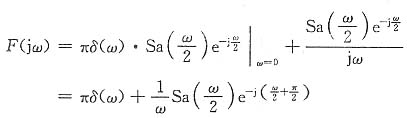
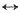 ej2ω-ejω-e-jω+e-j2ω
ej2ω-ejω-e-jω+e-j2ω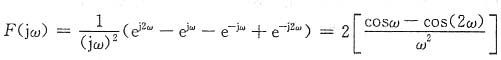
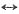 ejω-e-jω-jω(ejω+e-jω)=j2(sinω-ωcosω)
ejω-e-jω-jω(ejω+e-jω)=j2(sinω-ωcosω)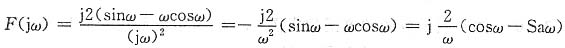
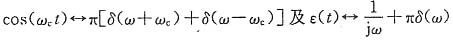 ,再利用频域卷积定理,有
,再利用频域卷积定理,有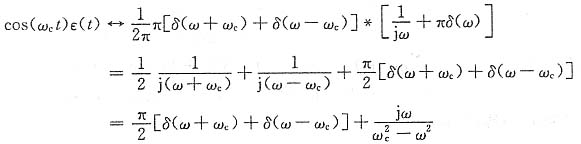
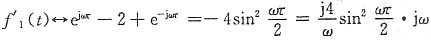
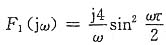
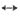 ej2ω+ejω-e-jω-e-j2ω=2j[sinω+sin(2ω)]
ej2ω+ejω-e-jω-e-j2ω=2j[sinω+sin(2ω)]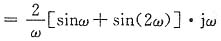
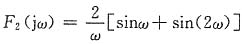
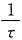 (t-τ)[ε(t)-ε(t-τ)]
(t-τ)[ε(t)-ε(t-τ)]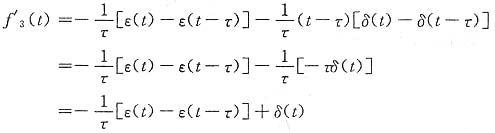
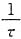 [δ(t)-δ(t-τ)]+δ'(t)
[δ(t)-δ(t-τ)]+δ'(t)