一、单项选择题(在每小题列出的四个备选项中只有一个是最符合题目要求的)
5. 曲线
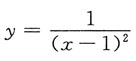
的渐近线的条数为______
A B C D
B
[考点] 曲线的渐近线
[解析] 因为
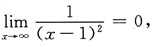
则原曲线有水平渐近线y=0，
因为
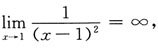
则原曲线有铅直渐近线x=1．
二、填空题1.
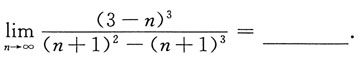
1
[考点] 函数极限的求法
[解析]
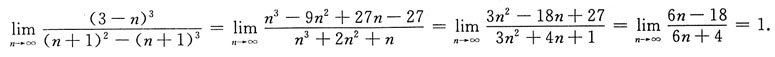
2. 函数
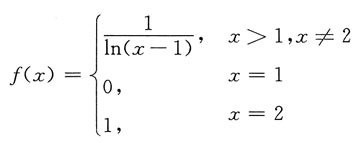
的连续区间为______．
[1，2)∪(2，+∞)
[考点] 分段函数的连续性
[解析] 由题意知：该分段函数在x=1，x=2时有不同的函数值．
因为
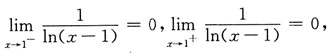
又因x=1时，f(x)=0，故在x=1处连续．
又因当x=2时，
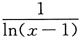
无意义，故连续区间为[1，2)∪(2，+∞)．
3. 设y=xsinx，则y"=______．
2cosx-xsinx
[考点] 二阶导数的求法
[解析] y'=(xsinx)'=sinx+xcosx，y"=(sinx+xcosx)'=2cosx-xsinx．
4. 设
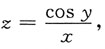
则全微分dz=______．
[考点] 全微分的求法
[解析]
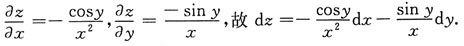
5.
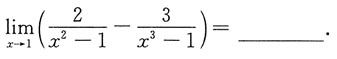
[考点] 极限的求法
[解析]
6. ∫2xe
2xdx=______．
[考点] 不定积分的计算
[解析]
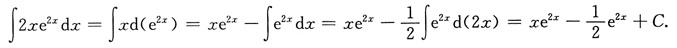
7. 函数f(x)=x-arcsinx的单调减少区间是______．
[-1，1]
[考点] 函数单调性的判定
[解析] 由题意得
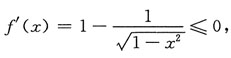
故1-x
2≤1．因x
2≥0，故1-x
2≤1恒成立，函数为单调递减函数．又因x的定义域为[-1，1]．故函数的单调递减区间为[-1，1]．
8. 函数y=|lnx|的上凸区间是______．
[1，+∞)
[考点] 曲线函数凹凸性的判定
[解析] 由题意得
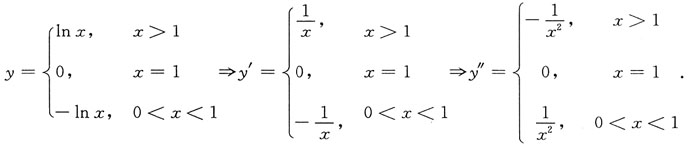
令y"≤0可得x≥1，则已知函数的凸区间为[1，+∞)．
10. 若D是由y=x，y=2x，x=1所围成的平面区域，则
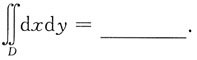
[考点] 二重积分的应用
[解析]
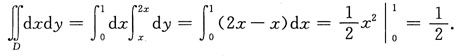
三、计算题(一)(每小题5分，共25分)
1. 设y=ln(cscx-cotx)，求y'．
解：
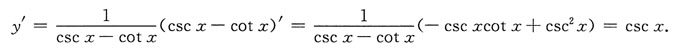
2. 求不定积分
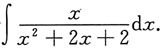
解：
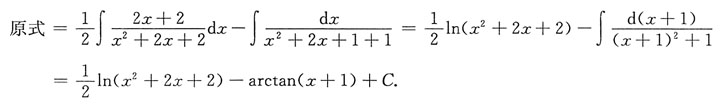
3. 求定积分
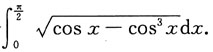
解：
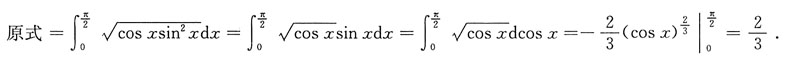
4. 已知过曲线y=f(x)上任意一点(x，y)处的切线斜率为e
2x，且曲线经过点
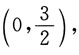
求该曲线方程．
解：由题设可得f'(x)=e
2x，则
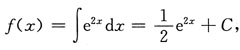
由曲线过点
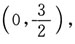
可得C=1．
因此，所求曲线方程为
5. 将下面的积分化为极坐标形式，并计算积分值：
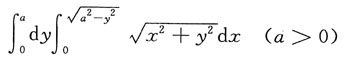
解：化为二重积分，D为圆心在(0，0)，半径为a的圆在第一象限的部分，
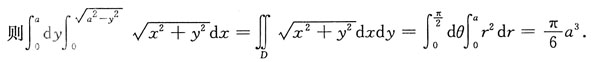
四、计算题(二)(每小题7分，共21分)
1. 方程xyz-ln(xyz)=1确定了隐函数z=z(x，y)，求
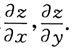
解：设F(x，y，z)=xyz-ln(xyz)-1，则
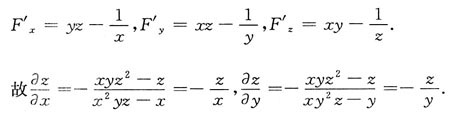
2. 求由圆面x
2+(y-b)
2≤a
2(0＜a＜b)绕x轴旋转一周所形成的物体的体积．
解：
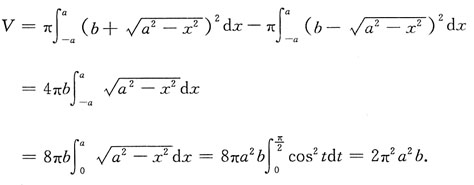
五、应用题(9分)
1. 设某商品每周生产x单位时，总成本为C(x)=100+2x，该产品的需求函数为x=800-100p(p为该商品单价)，求能使利润最大的p值．
解：
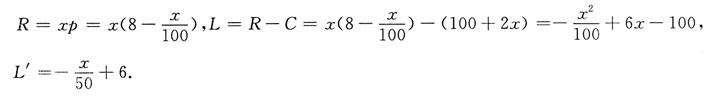
令L'=0，得驻点x=300，因为
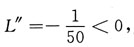
所以x=300是L的极大值点，也是最大值点，将x=300代入需求函数得p=5．
的定义域是______
在x=0处连续，则k=______
欲使f(x)在x=0处连续，只
需
则
的幂级数，并证明
深色：已答题 浅色：未答题