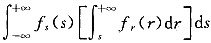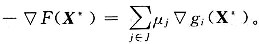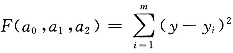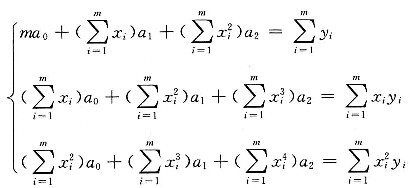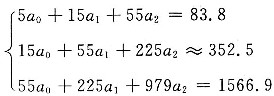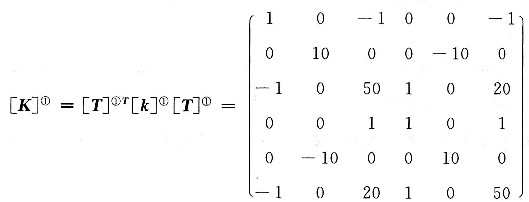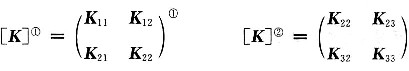第Ⅰ部分 选择题
一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)
8. 函数
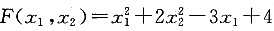
在点(1 1)
T处的梯度为______
- A.(-1 4)T
- B.(1 4)T
- C.(-2 -4)T
- D.(2 4)T
A B C D
A
[解析] 函数
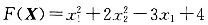
的一阶偏导为
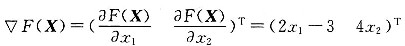
,当x
1-x
2=1时,即点(1 1)
T处,函数的梯度▽F(X)=(-1 4)
T。
14. 当零件材料强度的均值大于应力的均值时,零件的平均安全系数为
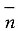
,失效概率为F,则______
A.
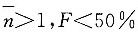
B.
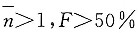
C.
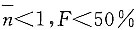
D.
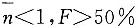
A B C D
A
[解析] 强度均值大于应力均值时,即μ
r>μ
s,平均安全系数
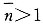
,失效概率F<50%;强度均值小于应力均值时,即μ
r<μ
s,平均安全系数
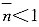
,失效概率F>50%。
二、多项选择题(在每小题列出的五个备选项中至少有两个是符合题目要求的。)
第Ⅱ部分 非选择题
三、填空题1. CAD系统的硬件组成很难有一个统一的标准,一个典型的CAD系统的基本硬件一般由主机、输入设备、输出设备和______设备及计算机网络等几部分组成。
2. 计算机的系统软件包括操作系统、汇编系统、______系统和诊断系统等。
3. 约束条件可分为______约束和性能约束两类。
4. 一维搜索方法中黄金分割法每次缩短后的新区间与原区间长度的比值始终是一个常数,此常数为______。
5. 用有限元法分析汽车车架的固有频率和振型,该问题属于______问题。
6. 无逆矩阵的矩阵称为奇异矩阵,其______的值等于零。
7. 产品在规定的条件下和规定的时间内完成规定功能的______称作产品的可靠度。
8. 某零件的强度和应力的分布密度函数分别为f
r(r)和f
s(s),则计算零件可靠度的一般方程为R=______。
四、简答题(每小题7分,共28分)
1. 常用数据模型有哪几种?各自有何特点?
(1)层次模型。指记录间是树型的组织结构,体现了记录间“一对多”的关系,具有结构简单、清晰的特点,适用于记录之间本身就存在一种自然的层次关系,但它难于处理记录之间复杂的联系。
(2)网络模型。指事物之间为网络的组织结构,体现了事物间的“多对多”的关系。能处理事物之间非常复杂的联系,模型结构极其复杂。
(3)关系模型。以集合论中的“关系”的概念为理论基础,把信息定义为一张二维表的组织结构,每一张表为一个关系,表中的每一行为一个记录,每一列为数据项。
2. 简述库恩—塔克条件及其几何意义。
库恩—塔克条件可表示为梯度形式,即
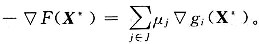
几何意义:在约束极小值X
*处,函数F(X)的负梯度一定能表示成所有起作用约束在该点梯度(法向量)的非负线性组合。
3. 简述可靠度分配的等同分配法和加权分配方法的原理和特点。
等同分配法:按照系统中各单元(子系统或零部件)的可靠度均相等的原则进行分配。计算简单,没有考虑各子系统现有的可靠度水平、重要性等因素。
加权分配法:把各子系统在整个系统中的重要度以各子系统的复杂度作为权重来分配可靠度。计算麻烦一些,但考虑了子系统的重要度。
4. 简述在有限元分析时,如何确定节点位置和单元数量。
节点的选择:若结构在几何形状、材料性质和外部条件无突变时,该结构应等分成几个单元,节点呈等距分布。若存在不连续性,节点应选在突变处。
单元数量:取决于要求的精度、单元的尺寸及自由度的数量。单元的数量越多精度越高,但这有一个界限。
五、计算题(共20分)
1. 将下列数据拟合成y=a
0+a
1x+a
2x
2形成的经验公式。(计算结果保留两位小数)
| xi | 1 | 2 | 3 | 4 | 5 |
| yi | 2.05 | 3.90 | 11.20 | 24.20 | 42.45 |
设经验公式为y=a
0+a
1x+a
2x
2,则节点的偏差平方和为:
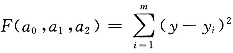
将F(a
0,a
1,a
2)分别对a
0,a
1,a
2求偏导并使其等于零,整理后得:
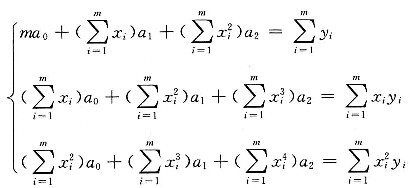
表中共有5组数据,故m=5
将表中数据和m=5代入上式得:
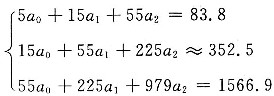
解此方程组,得:
a
0=5.68,a
1=-6.39,a
2=2.75
所以由表中数据拟合成的公式为:
y=2.75x
2-6.39x+5.68
2. 由相互垂直的两杆组成的平面刚架结构,节点编号单元编号如图示,在节点3上作用垂直向下的大小为100N的力,单元①和单元②在局部坐标系下的单元刚度矩阵相同,都为

引入支撑条件写出平衡方程。
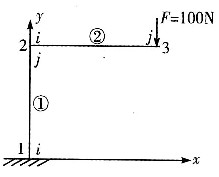
先求单元在总体坐标系下的单元刚度矩阵。
单元②局部坐标系下的单元刚度矩阵与总体坐标系下的单元刚度矩阵相同,即[K]
②=[k]
② 单元①的局部坐标系顺时针旋转90°就会与总体坐标系重合。
单元①的坐标转换矩阵为:

单元①在整体坐标系下的单元刚度矩阵为:
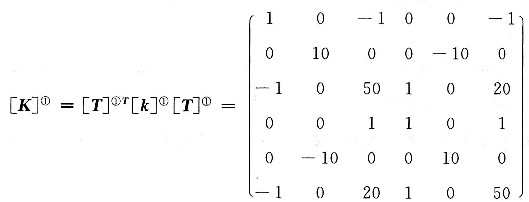
单元局部编码与总体编码的对应关系为:
单元①i j→1 2
单元②i j→2 3
单元刚度矩阵中子块对应关系为:
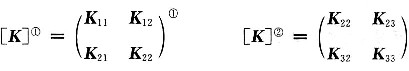
总体刚度矩阵为:

节点位移矢量为(U
1 V
1 θ
1 U
2 V
2 θ
2 U
3 V
3 θ
3)
T 节点力矢量为(F
1x F
1y M
1 F
2x F
2y M
2 F
3x F
3y M
3)
T 未引入支撑条件的总体平衡方程为:

约束条件为:U
1=0,V
1=0,θ=0。
作用在结构上的外力为F
3y=-100N,其余为零。
所以引入支撑条件后的结构平衡方程为:

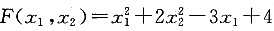 在点(1 1)T处的梯度为______
在点(1 1)T处的梯度为______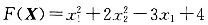 的一阶偏导为
的一阶偏导为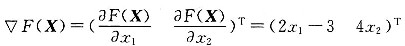 ,当x1-x2=1时,即点(1 1)T处,函数的梯度▽F(X)=(-1 4)T。
,当x1-x2=1时,即点(1 1)T处,函数的梯度▽F(X)=(-1 4)T。 ,失效概率为F,则______
,失效概率为F,则______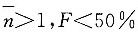
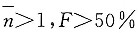
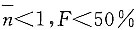
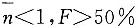
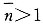 ,失效概率F<50%;强度均值小于应力均值时,即μr<μs,平均安全系数
,失效概率F<50%;强度均值小于应力均值时,即μr<μs,平均安全系数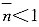 ,失效概率F>50%。
,失效概率F>50%。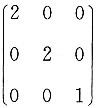

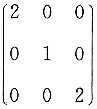
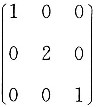

 ,可实现与E项相同结果的等比缩小。
,可实现与E项相同结果的等比缩小。