第Ⅰ部分 选择题
一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的)6. 设α,β是集合A上的相容关系,则下列关系不一定是相容关系的是______
A.α∪β
B.α∩β
C.
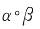
D.α
-1 A B C D
C
[解析] 举例说明,设α={〈1,1〉,〈1,2〉,〈2,1〉,〈2,2〉},β={〈2,3〉,〈3,2〉,〈2,2〉,〈3,3〉},则α,β均为相容关系,而
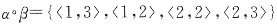
,显然
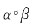
不是相容关系。
10. 下列语句是假命题的是______
A.只有2是奇数,
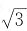
才是无理数
B.只要2是奇数,
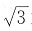
就是无理数
C.如果2是奇数,那么
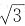
就是无理数
D.除非
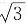
是无理数,否则2不是奇数
A B C D
A
[解析] 设P:2是奇数,Q:
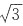
是无理数,则P为F,Q为T。选项A可符号化为“Q→P”,Q→P的真值为F,则选项A为假命题。选项B、C、D均可符号化为“P→Q”,P→Q的真值为T,即选项B、C、D均为真命题。
第Ⅱ部分 非选择题
二、填空题1. 公式
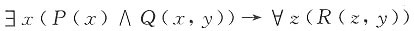
的约束变元为______,自由变元为______。
2. 设A={2,3,4,5},a*b=max(a,b)。代数系统〈A,*〉的幺元是______,零元是______。
3. 设无向树T有3个度数为3的结点,其余结点都为树叶,则T的结点数为______。
8
[解析] 设树T的树叶数为n,则树T有n+3个结点,n+2条边。由结点度数总和与边数的关系知n+3×3=2(n+2),故n=5,则树T的结点个数为5+3=8。
4. 命题公式﹁P∨Q∨﹁R的二进制编码大项M
i为______。
5. 设A={4,2,1},B={5,1,3},则B-A=______,B
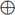
A=______。
6. 设F(x):x有进取心,要求只能使用全称量词,命题“某些人有进取心”可符号化为______。
7. 设A={a,b,c,d},B={1,2,3,4},A到B的关系R={〈a,4〉,〈b,1〉,〈b,2〉},B到A的关系S={〈4,a〉,〈3,b〉,〈2,c〉},则

8. 命题公式P∨(Q∧﹁R)的成真指派有______个,成假指派有______个。
5;3
[解析] 命题公式P∨(Q∧﹁R)的真值表如下表所示。
| P
|
Q
|
R
|
﹁R
|
Q∧﹁R
|
P∨(Q∧﹁R)
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
1
0
1
0
1
0
1
0
|
0
0
1
0
0
0
1
0
|
0
0
1
0
1
1
1
1
|
故公式P∨(Q∧﹁R)的成真指派有5个,成假指派有3个。
9. 设R={〈a,2〉,〈b,4〉,〈b,3〉,〈d,2〉}是集合A={a,b,c,d}到集合B={1,2,3,4}的关系,则ranR=______,domR=______。
10. 设S={φ,{1},(1,2)},则其幂集
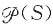
的元素个数为______。
8
[解析]
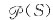
有2
3=8个元素。
三、计算题(每小题6分,共30分)1. 构造命题公式(﹁P→Q)∧(Q→R)的真值表。
| P
|
Q
|
R
|
﹁P
|
Q→R
|
﹁P→Q
|
(﹁P→Q)∧(Q→R)
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
1
1
1
1
0
0
0
0
|
1
1
1
0
1
1
0
1
|
0
0
1
1
1
1
1
1
|
0
0
0
1
1
1
0
1
|
2. 利用等值演算法求命题公式(﹁P∨Q)∧(R→﹁Q)的主析取范式。
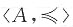 为偏序集,其哈斯图如下图所示。
为偏序集,其哈斯图如下图所示。
3. 写出偏序关系
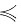
;
偏序关系
4. 设B={b,d,e},求B的极大元、极小元、上界和下界。
B的极大元:d,e;
极小元:b;
上界:g;
下界:b,a。
5. 写出由S导出的A上的等价关系ρ的有序对集合;
ρ=({1,2}×{1,2})∪({3}×{3})∪({4,5}×{4,5})
={〈1,1〉,〈1,2〉,〈2,1〉,〈2,2〉,〈3,3〉,〈4,4〉,〈4,5〉,〈5,4〉,〈5,5〉};
6. 写出ρ的关系矩阵。
ρ的关系矩阵为

7. 设解释I如下:D={2,3},已知F(2,2)=F(3,3)=0,F(2,3)=F(3,2)=1,f(2,2)=f(2,3)=2,f(3,2)=f(3,3)=3。
求谓词公式
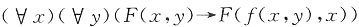
在I下的真值。
四、证明题(每小题7分,共21分)1. 设A,B,C是集合。证明:(A-B)-C=A-(B∪C)。
证明:
(1)若x∈(A-B)-C,则x∈A-B但
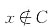
,
即x∈A但
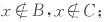
即x∈A但
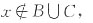
即x∈A-(B∪C);
所以
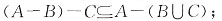
(2)若x∈A-(B∪C),则x∈A但
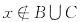
;
即x∈A但
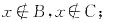
即x∈A-B但
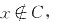
即x∈(A-B)-C;
所以
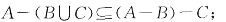
(3)因此,(A-B)-C=A-(B∪C)。
2. 设无向简单图G有9个结点。证明:G中至少存在两个度数相同的结点。
证明:由于G是有9个结点的无向简单图,
所以G的结点的度数只能为0,1,2,3,4,5,6,7,8这9种情况。
但是,度数为0和度数为8不能同时出现,
因此,G的结点的度数最多有8种不同的值。
由于G有9个结点,所以至少有两个结点的度数相同。
3. 设〈G,·〉是群,
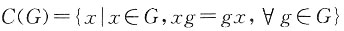
。证明:〈C(G),·〉是〈G,·〉的一个子群。
证明:〈G,·〉是群,设e是G的单位元。显然e∈C(G)。
对任意的m,n∈C(G),对任意的g∈G,
有(mn)g=m(gn)=g(mn),
所以mn∈C(G)。
又由mg=gm可得gm-1=m-1g,
所以m-1∈C(G)。
因此〈C(G),·〉是〈G,·〉的一个子群。
五、综合应用题(每小题7分,共14分)1. 符号化下列命题,并构造推理证明。
每个学生都是勤奋的;每个勤奋而又聪明的人在他的工作生活中都将获得成功;小华是学生,并且是聪明的。所以,小华在他的工作生活中将获得成功。
解:设个体域为全体人类。
a:小华;
M(x):x是学生;
H(x):x是勤奋的;
G(x):x是聪明的;
R(x):x在工作生活中将获得成功。

2. 今有a,b,c,d,e,f,g共7人,已知下列事实:
a会讲法语;b会讲法语、意大利语和日语;c会讲法语、汉语;d会讲日语和意大利语;e会讲德语、汉语和法语;f会讲英语、日语和俄语;g会讲英语和德语。试问:这7个人应如何围圆桌排座位,才能使每个人和他两边的人可以交谈?(须写出所有可能方案)
设无向图G=〈V,E〉,其中
V={a,b,c,d,e,f,g},
E={(u,v)|u,v∈V,且u和v有共同语言};
作图如下图所示。
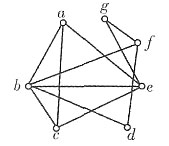
将这七人排座围圆桌而坐,使得每个人与身边人都能交谈,
即在上图中寻找哈密顿回路;
经观察哈密顿回路有:aegfdbca,acegfdba,acbdfgea,abdfgeca(实际有两个不同的哈密顿回路),依此次序围圆桌安排座位即可。
 是一个偏序集,其中A是正整数12的正因子的集合,
是一个偏序集,其中A是正整数12的正因子的集合,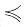 为整除关系,元素6能盖住元素______
为整除关系,元素6能盖住元素______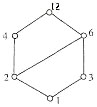 ,其覆盖关系为:12覆盖4、6,4、6覆盖2,6覆盖2、3,2、3覆盖1。
,其覆盖关系为:12覆盖4、6,4、6覆盖2,6覆盖2、3,2、3覆盖1。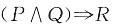
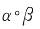
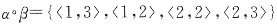 ,显然
,显然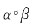 不是相容关系。
不是相容关系。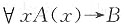 等价的是______
等价的是______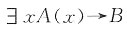
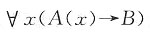
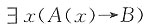
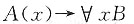
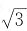 才是无理数
才是无理数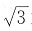 就是无理数
就是无理数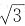 就是无理数
就是无理数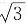 是无理数,否则2不是奇数
是无理数,否则2不是奇数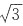 是无理数,则P为F,Q为T。选项A可符号化为“Q→P”,Q→P的真值为F,则选项A为假命题。选项B、C、D均可符号化为“P→Q”,P→Q的真值为T,即选项B、C、D均为真命题。
是无理数,则P为F,Q为T。选项A可符号化为“Q→P”,Q→P的真值为F,则选项A为假命题。选项B、C、D均可符号化为“P→Q”,P→Q的真值为T,即选项B、C、D均为真命题。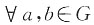 有______
有______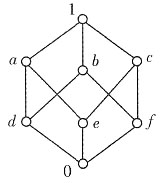
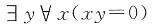

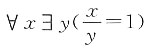
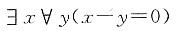
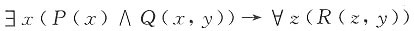 的约束变元为______,自由变元为______。
的约束变元为______,自由变元为______。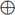 A=______。
A=______。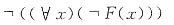

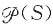 的元素个数为______。
的元素个数为______。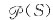 有23=8个元素。
有23=8个元素。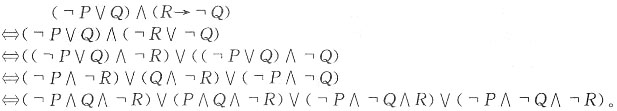
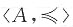 为偏序集,其哈斯图如下图所示。
为偏序集,其哈斯图如下图所示。
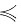 ;
;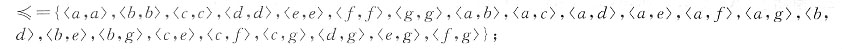

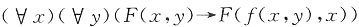 在I下的真值。
在I下的真值。
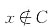 ,
,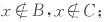
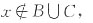
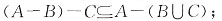
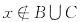 ;
;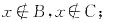
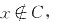
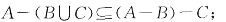
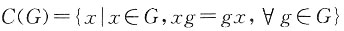 。证明:〈C(G),·〉是〈G,·〉的一个子群。
。证明:〈C(G),·〉是〈G,·〉的一个子群。

