第Ⅰ部分 选择题
一、单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的。
第Ⅱ部分 非选择题
二、填空题2. 已知自由落体冲击时的动荷因数为K
d,对应静载荷的最大位移为Δ
jmax,自由落体的高度h,则冲击问题的最大位移可以表示为______。
5. 在单元体互相垂直的截面上,垂直于截面交线的切应力的必定成对存在,大小相等,方向则______。
6. 自由落体冲击问题的动荷系数为
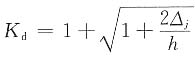
,其中h表示______。
7. 对于一般钢试件,循环基数N
0的数值为______。
9. 低碳钢的应力—应变曲线如图所示,其上______点的纵坐标值为该钢的强度极限σ
b。
10. 若材料服从胡克定律,且物体的变形满足小变形,则该物体的变形量与载荷之间呈现______关系。
11. 图示正方形截面简支梁,若载荷不变而将截面边长增加一倍,则其最大弯曲正应力为原来的______倍,最大弯曲切应力为原来的
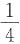
倍。
12. 将圆截面压杆改为面积相等的圆环截面压杆,其他条件不变,则其柔度将降低,临界载荷将______。
13. 第三强度理论和第四强度理论的相当应力分别为σ
r3和σ
r4,对于纯剪切状态,恒有σ
r3/σ
r4=______。
14. 根据支座的类型和位置,静定梁可分为三种基本形式:______、外伸梁、悬臂梁。
15. 在所截截面的内侧取微段,凡使微段产生顺时针转动趋势的剪力为______;使微段弯曲变形后,凹面朝向下的弯矩为负。
三、计算题(每小题6分,共30分)
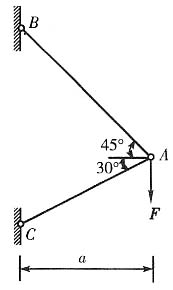
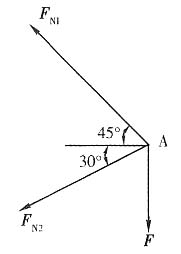
1. 如图所示已知AB、AC杆均为相同材料的圆截面杆。要求在力F的作用下,A点不发生水平位移,试求两杆的直径之比。
以结点A为研究对象,受力分析如下图所示。
并设AB杆为1杆,AC杆为2杆。
由∑F
x=0,得
-F
N1cos45°-F
N2cos30°=0
由∑F
y=0,得
F
N1sin45°-F
N2sin30°-F=0
解以上两方程,得
F
N1=0.897F F
N2=-0.732F
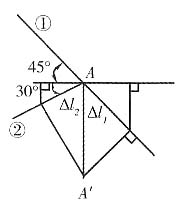
作结点A的位移如下图所示,其中A'为结点A的经过移动后的位置。
结点A不发生水平位移的条件为
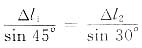
由胡克定律,得
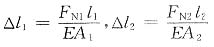
且
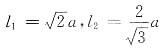
则
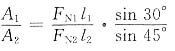
解得
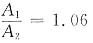
则
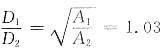
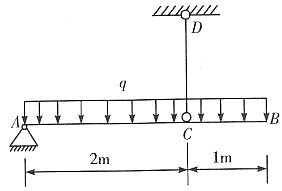
2. 试求许用荷载[q]。
内力分析
由∑M
A(F)=0,得
F
CD×2-q×3×(1+2)/2=0
则F
CD=2.25q
在q荷载单独作用下,距端点B为x处切取截面,并取右半段,建立弯矩方程:
M
1(x)=-0.5qx
2(0≤x<3)
在F
CD单独作用下,距端点B为x处切取截面,并取右半段,建立弯矩方程:
M
2(x)=2.25q(x-1)(1≤x<3)
根据叠加原理,则合弯矩为:
M(x)=M
1(x)+M
2(x)=-0.5qx
2+2.25q(x-1)(1≤x<3)
计算特征点:
x=0 M(0)=0
x=1 M(1)=-0.5q
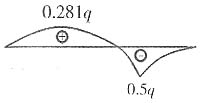
x=1.5 M(1.5)=0[由M(x)=0进行计算,解得x=1.5和x=3]
x=2.25 M(2.25)=0.281q[由M'(x)=0计算最大正弯矩,解得x=2.25]
弯矩图为
|M|
max=0.5q(C截面处)
按AB梁的强度条件确定许用荷载[q]。
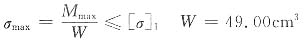
则[q]≤15.7kN/m
按拉杆CD的强度条件确定许用荷载[q]。
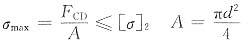
则[q]≤4.19kN/m
综合考虑梁和拉杆的强度,该结构的许用荷载[q]=4.19kN/m。即由拉杆的强度条件决定。
3. 为了提高此结构的承载能力,可改变哪一根杆件的截面尺寸?此时,尺寸多大为宜?而此时的许用荷载[q]又为多大?
为了提高结构的承载能力,应采用直径较大的拉杆,设直径为D,此时,拉杆和梁内的最大正应力均达到各自的许用应力。
梁上的荷载[q]=15.7kN/m时拉杆的拉力为F
CD=2.25q=35.3kN
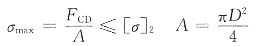
则D≥19.4mm
即当D=19.4mm时,结构的许用载荷为[q]为15.7kN/m。
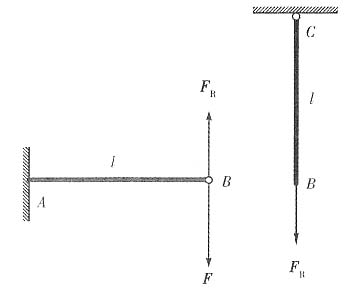
4. 如图所示一悬臂梁AB,承受集中载荷F的作用,因其刚度不够,用杆CB加固如图示,试计算梁AB的最大挠度的减少量。设梁与杆的刚度相同,分别为EI和EA,且A=3I/l
2。已知在集中力F作用下的悬臂梁的挠度公式为:
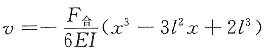
。
选择铰链B为约束,以相应的力F
R代替其作用,则原结构的等效结构如图示。
在力F
R作用下,杆CB的横截面B将铅垂下移,设其位移为s
1;而在载荷F和F
R作用下,梁的横截面B也将铅垂下移,设其位移为s
2。
由题意得s
1=s
2 对CB杆,由胡克定律,得
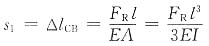
对AB梁,由集中力F
合作用下的悬臂梁的挠度公式,得
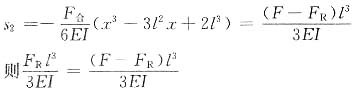
故F
R=F/2
梁AB未加固时,梁的最大挠度为
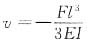
加固后梁的最大挠度为

即加固后,梁的最大挠度可减少50%。
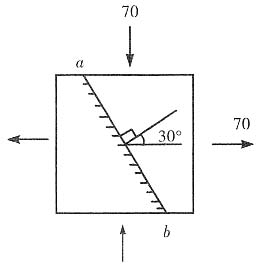
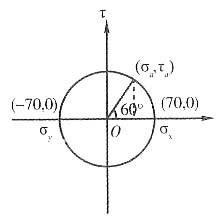
5. 已知单元体的应力状态如图所示,试用解析法和图解法(只要求示意图)求斜截面ab上的应力。应力的单位为MPa。
根据图示,有
σ
x=70MPa,σ
y=-70MPa,τ
xy=0,α=30°
由斜截面上的应力公式,得
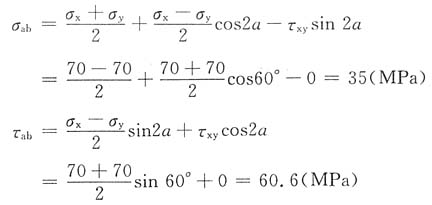
图解法如下图所示:
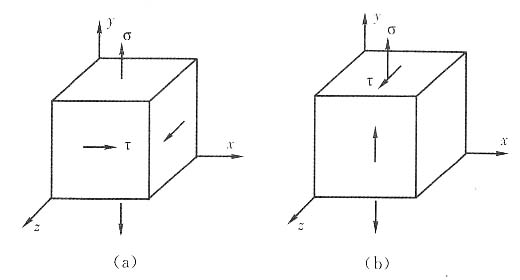
6. 如图(a)、(b)表示同一材料的两个单元体。材料的屈服极限σ
s=275MPa。试根据第三强度理论分别求出两个单元体同时进入屈服极限时的拉应力σ与切应力τ的值。设σ>τ。
单元体(a)的应力状态
σ
x=σ
z=0,σ
y=σ,xoz面上的切应力为0,故σ
y为其中一个主应力。
另外两个主应力为:
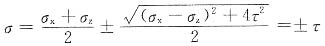
因σ>τ
所以主应力分别为σ
1=σ,σ
2=τ,σ
3=-τ
则由第三强度理论有
σ
r3=σ
1-σ
3=σ+τ≤[σ]
单元体(b)的应力状态
σ
x=σ
z=0,σ
y=σ,yoz面上的切应力为0,所以此面为主应力面,面上的应力为主应力,另外两个主应力为:
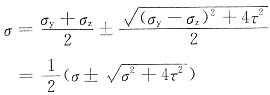
所以主应力分别为
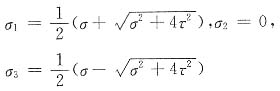
则由第三强度理论有
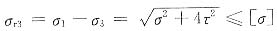
当两个单元体同时进入屈服极限时,可得
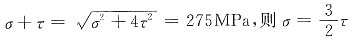
解得σ=165MPa,τ=110MPa
四、综合应用题(每小题10分,共20分)
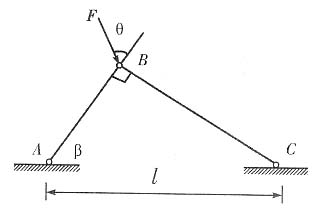
1. 如图所示铰接杆系ABC中,AB和BC均为细长压杆,且截面相同,材料一样。若因在ABC平面内失稳而破坏,并规定0<θ<π/2,试确定F为最大值时θ的大小。
AB和BC杆同时达到临界载荷时F为最大。
BC杆的临界载荷为
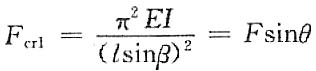
AB杆的临界截荷为
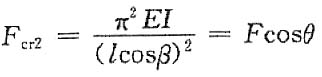
则
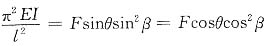
所以有
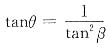
即θ=arctan(cot
2β)。
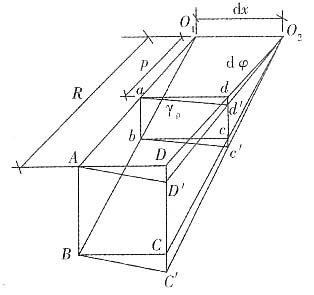
2. 试推导实心圆轴扭转切应力的一般公式,并指出切应力最大的位置,同时画出圆轴横截面上的切应力的分布草图。
根据圆轴扭转的平面假设,取相距为dx的两个横截面及夹角无限小的径向纵截面,从轴内取一楔形体O
1ABCDO
2,如下图所示。
设上述楔形体左右两横截面间的相对扭转角为dφ,矩形abcd的切应变为γ
ρ,则由图中的几何关系可知γ
ρ=tanγ
ρ=

即γ
ρ=
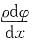
由剪切胡克定律可知,在横截面ρ处的切应力为
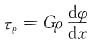
,方向垂直于该点处半径方向,如下图所示:
在距圆心为ρ处的微面积dA上,作用有微剪力τ
ρdA,它对圆心的力矩为ρτ
ρdA。在整个截面上,所有微力矩之和应等于该截面的扭矩T,即
∫
Aρτ
ρdA=T
代入上式,得
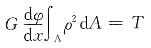
因I
P=∫
Aρ
2dA仅与截面的尺寸有关,
且为极惯性矩,则
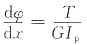
即为圆轴扭转变形的基本公式。
代入前式,得
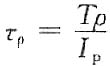
即为圆轴扭转切应力的一般公式。
当ρ=R时,
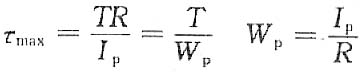
为抗扭截面系数。
横截面上的切应力的分布草图如下图所示:
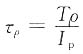 适用于下列哪种截面轴______
适用于下列哪种截面轴______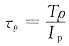 为圆轴扭转时横截面上切应力的计算公式,故正确答案为C。
为圆轴扭转时横截面上切应力的计算公式,故正确答案为C。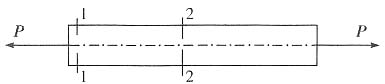
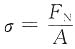 的应用条件是______
的应用条件是______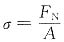 的应用条件是外力合力作用线必须沿着杆的轴线,故正确答案为C。
的应用条件是外力合力作用线必须沿着杆的轴线,故正确答案为C。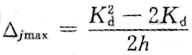
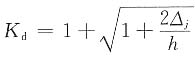 ,其中h表示______。
,其中h表示______。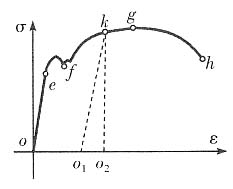
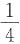 倍。
倍。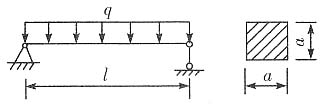
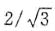
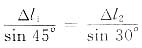
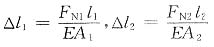
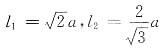
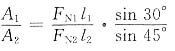
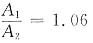
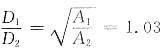
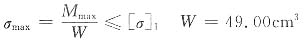
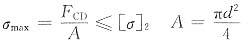
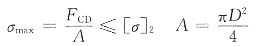
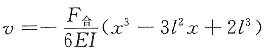 。
。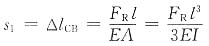
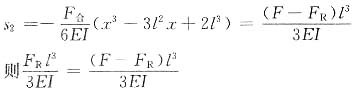
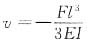

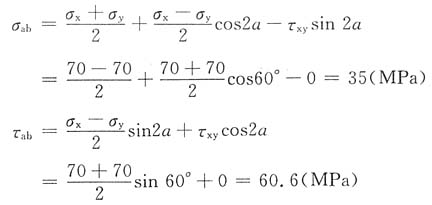
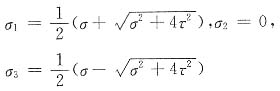
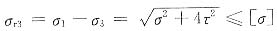
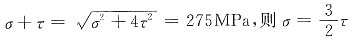
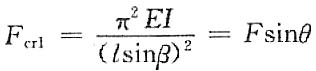
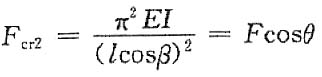
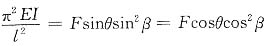
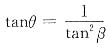

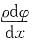
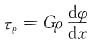 ,方向垂直于该点处半径方向,如下图所示:
,方向垂直于该点处半径方向,如下图所示: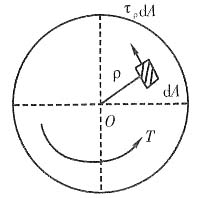
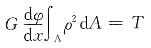
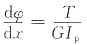 即为圆轴扭转变形的基本公式。
即为圆轴扭转变形的基本公式。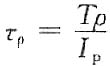 即为圆轴扭转切应力的一般公式。
即为圆轴扭转切应力的一般公式。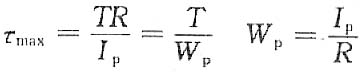 为抗扭截面系数。
为抗扭截面系数。