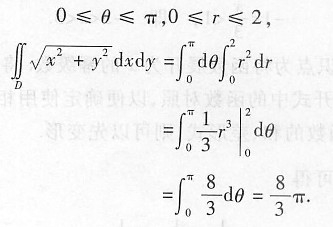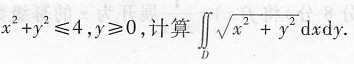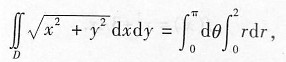一、选择题1~10小题,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设函数

在x=0处连续,则a等于
.
A.0 B.
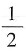
C.1 D.2
A B C D
C
本题考查的知识点为函数连续性的概念.
由函数连续性的定义可知,若f(x)在x=0处连续,则有
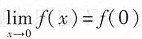
,由题设f(0)=a,
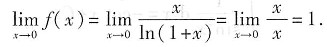
可知应有a=1,故应选C.
4. 设f(x)为连续函数,则(
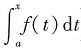
)'等于
.
A.f(t) B.f(t)-f(a) C.f(x)D.f(x)-f(a)
A B C D
C
本题考查的知识点为可变上限积分的求导性质.
这是一个基本性质:若f(x)为连续函数,则
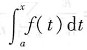
必定可导,且
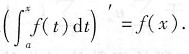
本题常见的错误是选D,这是由于考生将积分的性质

与牛顿-莱布尼茨公式
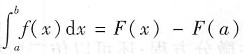
混在了一起而引起的错误.
7. 平面
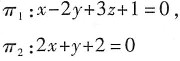
的位置关系为
.
A B C D
A
本题考查的知识点为两平面的关系.
两平面的关系可由两平面的法向量,n
1,n
2间的关系确定.
若n
1⊥n
2,则两平面必定垂直.
若
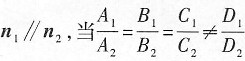
时,两平面平行;
当
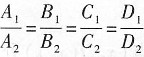
时,两平面重合.
若n
1与n
2既不垂直,也不平行,则两平面斜交.
由于n
1=(1,-2,3),n
2=(2,1,0),n
1·n
2=0,可知n
1⊥n
2,因此π
1⊥π
2,应选A.
10. 微分方程y'+y=0的通解为
.
- A.y=ex
- B.y=e-x
- C.y=Cex
- D.y=Ce-x
A B C D
D
本题考查的知识点为一阶微分方程的求解.
可以将方程认作可分离变量方程;也可以将方程认作一阶线性微分方程;还可以仿二阶线性常系数齐次微分方程,并作为特例求解.
解法1 将方程认作可分离变量方程.
分离变量
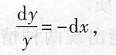
两端分别积分
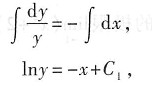
或 y=Ce
-x.
解法2 将方程认作一阶线性微分方程.由通解公式可得
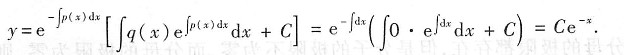
解法3 认作二阶常系数线性齐次微分方程特例求解:
特征方程为r+1=0,
特征根为 r=-1,
方程通解为 y=Ce
-x.
二、填空题1.
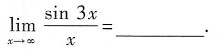
0
[解析] 本题考查的知识点为无穷小的性质.
对于
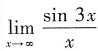
,其极限过程为x→∞,可知所给极限不能利用重要极限公式

这是考生经常犯错误的题目.
当x→∞时,sin3x不存在极限.由于当x→∞时,
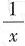
为无穷小,且sin3x为有界变量,由于“有界变量与无穷小之积仍为无穷小”,
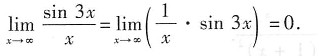
2.

2
[解析] 本题考查的知识点为极限的运算.
由于分子的极限
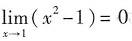
,分母的极限
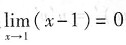
,因此所给极限不能利用极限的商的运算法则来求解.
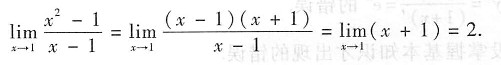
或利用洛必达法则可得
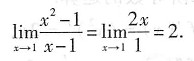
注:如果题目换为求
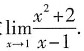
由于分母极限为0,分子极限为3,同样不能利用极限商的运算法则,此时可以利用无穷小量与无穷大量关系求解.
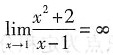
表示当x→1时,变量
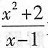
为无穷大,极限不存在.
这里常见的错误是直接利用洛必达法则:
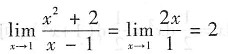
而导致错误.事实上,所给极限分子的极限
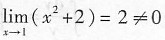
,因此所给函数极限不为“
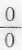
”型,不能利用洛必达法则求解.
如果计算极限,应该先判定其类型,再选择计算方法.当所求极限为分式时:
若分子与分母的极限都存在,且分母的极限不为零,则可以利用极限的商的运算法则求极限.
若分子与分母的极限都存在,但是分子的极限不为零,而分母的极限为零,则所求极限为无穷大.
若分子与分母的极限都为零,所给极限为“
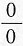
”型,则可以考虑利用洛必达法则,但此时应该检查是否满足洛必达法则的其他条件,是否可以进行等价无穷小代换,所求极限的分子或分母是否有非零因子,可以单独进行极限运算等.
3.
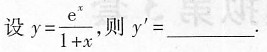
[解析] 本题考查的知识点为函数商的求导运算.
考生只需熟记导数运算的法则
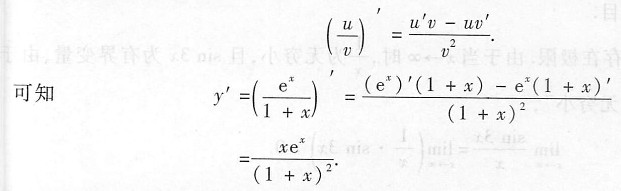
本题中有些考生还不会运用求导法则,误以为
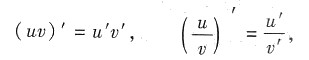
因此出现
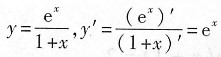
的错误.
这是由于考生没掌握基本知识才出现的错误.
4.
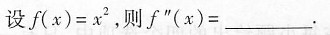
2
[解析] 本题考查的知识点为二阶导数的运算.
f'(x)=(x2)'=2x,
f"(x)=(2x)'=2.
5.
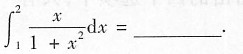
[解析] 本题考查的知识点为定积分的换元法.
由于被积函数
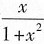
分母为二次函数,分子为一次函数,本例有多种解法.
解法1 利用凑微分,注意到
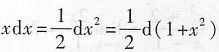
,可得

解法2令t=1+x
2,则dt=2xdx.
当x=1时,t=2;当x=2时,t=5.
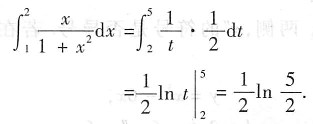
有的考生填为

,这个错误的原因是引入变量t=1+x
2,则dt=2xdx.得到
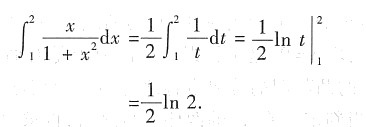
这里的错误在于进行定积分变量替换,积分区间没做变化.
6.
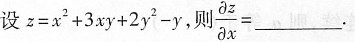
2x+3y
[解析] 本题考查的知识点为偏导数的运算.
由于z=x
2+3xy+2y
2-y,可得
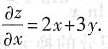
7.
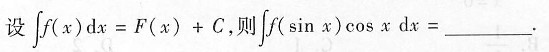
F(sinx)+C
[解析] 本题考查的知识点为不定积分的换元法.
由于∫f(x)dx=F(x)+C,令u=sinx,则du=cosxdx,
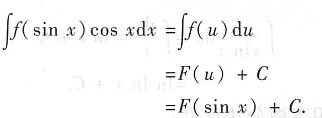
8. 幂级数
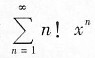
的收敛半径为______.
0
[解析] 本题考查的知识点为幂级数的收敛半径.
所给幂级数为不缺项情形

因此收敛半径为0.
9. 微分方程y'+9y=0的通解为______.
y=Ce-9x
[解析] 本题考查的知识点为求解可分离变量微分方程.
分离变量
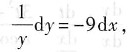
两端分别积分
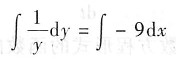
lny=-9x+C
1,y=Ce
-9x.
10. 曲线y=x
3-6x的拐点坐标为______.
(0,0)
[解析] 本题考查的知识点为求曲线的拐点.
依求曲线拐点的一般步骤,只需
(1)先求出y".
(2)令y"=0得出x1,…,xk.
(3)判定在点x1,x2,…,xk两侧,y"的符号是否异号.若在xk的两侧y"异号,则点(xk,f(xk)为曲线y=f(x)的拐点.
y=x3-6x,
y'=3x2-6,y"=6x.
令y"=0,得到x=0.当x=0时,y=0.
当x<0时,y"<0;当x>0时,y">0.因此点(0,0)为曲线y=x3-6x的拐点.
本题出现较多的错误为:填x=0.这个错误产生的原因是对曲线拐点的概念不清楚.拐点的定义是:连续曲线y=f(x)上的凸与凹的分界点称之为曲线的拐点.其一般形式为(x0,f(x0)),这是应该引起注意的,也就是当判定y"在x0的两侧异号之后,再求出f(x0),则拐点为(x0,f(x0)).
注意极值点与拐点的不同之处!
三、解答题21~28小题,解答时应写出推理、演算步骤.
1. 计算
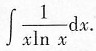
[解析] 本题考查的知识点为不定积分的换元积分运算.
注意
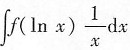
,通常引入变换t=lnx.
本例求
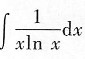
,可以令t=lnx,则
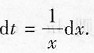
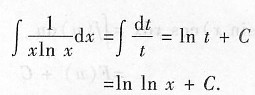
也可以不写出新变元,利用凑微分法计算:
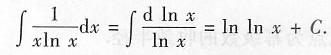
本题中出现的主要问题是不定积分运算丢掉任意常数C.
2. 设
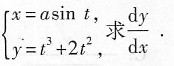
[解析] 本题考查的知识点为参数方程形式的函数的求导.
只需依公式
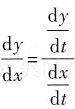
,先分别求出

即可.
3. 设z=xy
3+2yx
2求
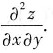
5. 将
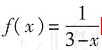
展开为x的幂级数.
[解析] 本题考查的知识点为将函数展开为x的幂级数.将函数展开为x的幂级数通常利用间接法.先将f(x)与标准展开式中的函数对照,以便确定使用相应的公式.如果f(x)可以经过恒等变形变为标准展开式中函数的和、差形式,则可以先变形.
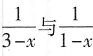
相近,恒等变形可得
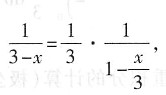
将
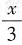
认作整体,则可以利用标准展开式
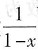
求解.
需要指出的问题是,不要丢掉收敛区间
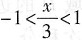
.这是考生中常常出现的问题.
6. 设
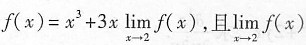
存在,求f(x).
[解析] 本题考查的知识点为两个:极限的运算;极限值是个确定的数值.
设
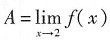
是本题求解的关键.未知函数f(x)在极限号内或f(x)在定积分号内的、以方程形式出现的这类问题,求解的基本思想是一样的.请读者明确并记住这种求解的基本思想.
本题考生中多数人不会计算,感到无从下手.考生应该记住这类题目的解题关键在于明确:
如果
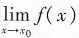
存在,则
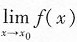
表示一个确定的数值.
7. 求曲线y=x
2+1在点(1,2)处的切线方程.并求该曲线与所求切线及x=0所围成的平面图形的面积.
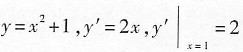
,因此曲线y=X
2+1在点(1,2)处的切线方程为
y-2=2(x-1),
y=2x.
曲线y=x
2+1,切线y=2x与x=0所围成的平面图形如图3-1所示.
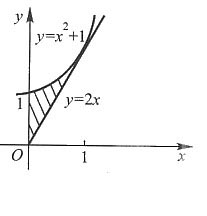
其面积

[解析] 本题考查的知识点为:求曲线的切线方程;利用定积分求平面图形的面积.
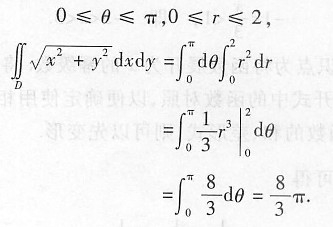
8. 设区域D为:
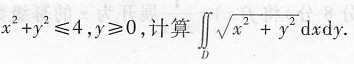
利用极坐标,区域D可以表示为
[解析] 本题考查的知识点为二重积分的计算(极坐标系).
如果积分区域为圆域或圆的一部分,被积函数为f(x
2+y
2)的二重积分,通常利用极坐标计算较方便.
使用极坐标计算二重积分时,要先将区域D的边界曲线化为极坐标下的方程表示,以确定出区域D的不等式表示式,再将积分化为二次积分.
本题考生中常见的错误为:
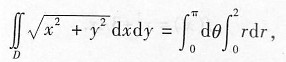
被积函数中丢掉了r.这是将直角坐标系下的二重积分化为极坐标下的二次积分时常见的错误,考生务必要注意.
 在x=0处连续,则a等于 .
在x=0处连续,则a等于 .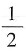 C.1 D.2
C.1 D.2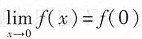 ,由题设f(0)=a,
,由题设f(0)=a,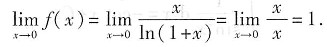
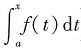 )'等于 .
)'等于 .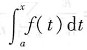 必定可导,且
必定可导,且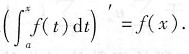
 与牛顿-莱布尼茨公式
与牛顿-莱布尼茨公式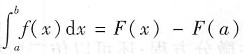 混在了一起而引起的错误.
混在了一起而引起的错误. 等于( ).
等于( ).
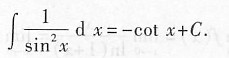
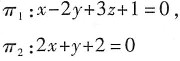 的位置关系为 .
的位置关系为 .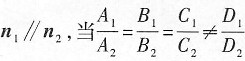 时,两平面平行;
时,两平面平行;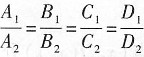 时,两平面重合.
时,两平面重合.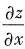 等于( ).
等于( ).
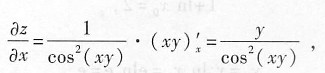
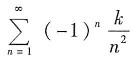 (k为非零正常数) .
(k为非零正常数) .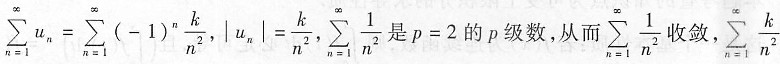 收敛,可知所给级数绝对收敛.
收敛,可知所给级数绝对收敛.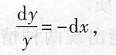
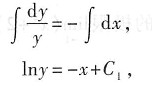
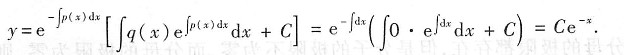
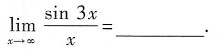
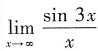 ,其极限过程为x→∞,可知所给极限不能利用重要极限公式
,其极限过程为x→∞,可知所给极限不能利用重要极限公式 这是考生经常犯错误的题目.
这是考生经常犯错误的题目.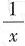 为无穷小,且sin3x为有界变量,由于“有界变量与无穷小之积仍为无穷小”,
为无穷小,且sin3x为有界变量,由于“有界变量与无穷小之积仍为无穷小”,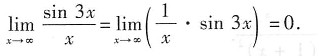

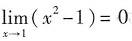 ,分母的极限
,分母的极限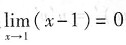 ,因此所给极限不能利用极限的商的运算法则来求解.
,因此所给极限不能利用极限的商的运算法则来求解.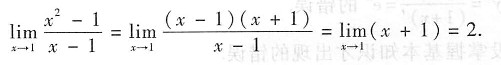
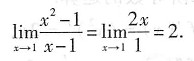
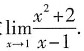 由于分母极限为0,分子极限为3,同样不能利用极限商的运算法则,此时可以利用无穷小量与无穷大量关系求解.
由于分母极限为0,分子极限为3,同样不能利用极限商的运算法则,此时可以利用无穷小量与无穷大量关系求解.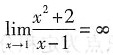 表示当x→1时,变量
表示当x→1时,变量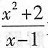 为无穷大,极限不存在.
为无穷大,极限不存在.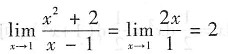
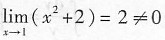 ,因此所给函数极限不为“
,因此所给函数极限不为“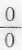 ”型,不能利用洛必达法则求解.
”型,不能利用洛必达法则求解.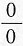 ”型,则可以考虑利用洛必达法则,但此时应该检查是否满足洛必达法则的其他条件,是否可以进行等价无穷小代换,所求极限的分子或分母是否有非零因子,可以单独进行极限运算等.
”型,则可以考虑利用洛必达法则,但此时应该检查是否满足洛必达法则的其他条件,是否可以进行等价无穷小代换,所求极限的分子或分母是否有非零因子,可以单独进行极限运算等.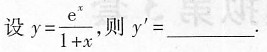
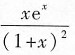
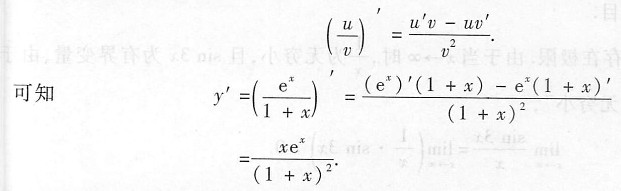
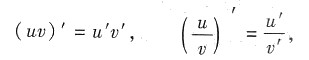
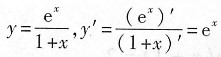 的错误.
的错误.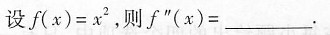
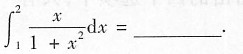
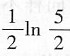
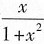 分母为二次函数,分子为一次函数,本例有多种解法.
分母为二次函数,分子为一次函数,本例有多种解法.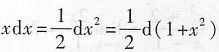 ,可得
,可得
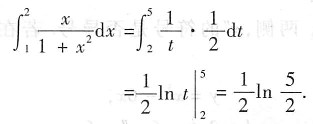
 ,这个错误的原因是引入变量t=1+x2,则dt=2xdx.得到
,这个错误的原因是引入变量t=1+x2,则dt=2xdx.得到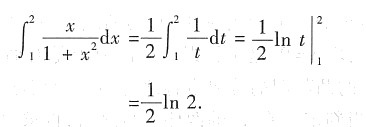
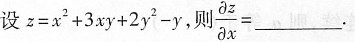
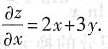
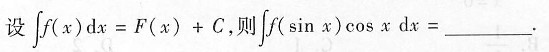
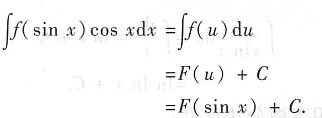
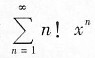 的收敛半径为______.
的收敛半径为______.
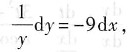
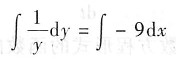
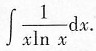
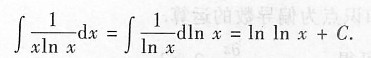
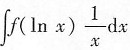 ,通常引入变换t=lnx.
,通常引入变换t=lnx.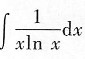 ,可以令t=lnx,则
,可以令t=lnx,则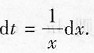
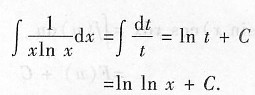
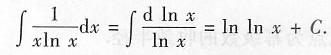
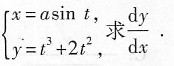
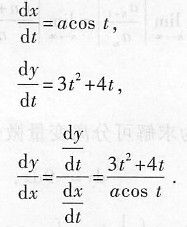
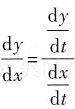 ,先分别求出
,先分别求出 即可.
即可.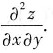
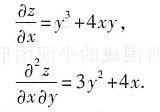
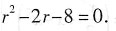
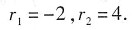
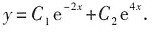
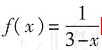 展开为x的幂级数.
展开为x的幂级数.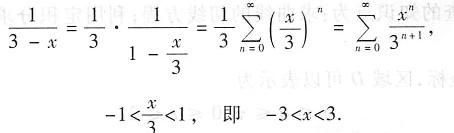
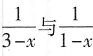 相近,恒等变形可得
相近,恒等变形可得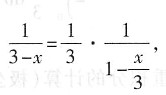
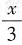 认作整体,则可以利用标准展开式
认作整体,则可以利用标准展开式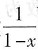 求解.
求解.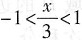 .这是考生中常常出现的问题.
.这是考生中常常出现的问题.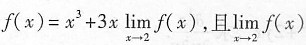 存在,求f(x).
存在,求f(x). ,则
,则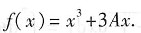
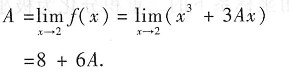
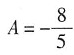 ,因此
,因此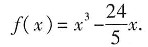
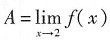 是本题求解的关键.未知函数f(x)在极限号内或f(x)在定积分号内的、以方程形式出现的这类问题,求解的基本思想是一样的.请读者明确并记住这种求解的基本思想.
是本题求解的关键.未知函数f(x)在极限号内或f(x)在定积分号内的、以方程形式出现的这类问题,求解的基本思想是一样的.请读者明确并记住这种求解的基本思想.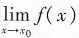 存在,则
存在,则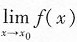 表示一个确定的数值.
表示一个确定的数值.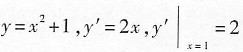 ,因此曲线y=X2+1在点(1,2)处的切线方程为
,因此曲线y=X2+1在点(1,2)处的切线方程为