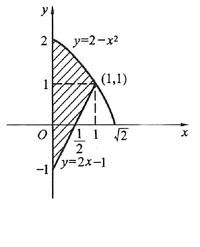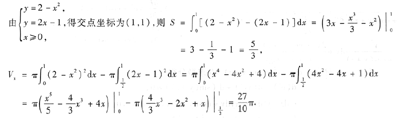一、选择题在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内 二、填空题把答案填在题中横线上1.

[[分析] 计算极限时一定要注意极限的不同类型,当x→0时,本题不是“
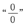
”型,所以直接利用极限的四则运算法则计算即可.但当x→1时,本题是“
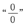
”型,可用因式分解消去零因式等方法求解.
2.
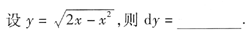
答
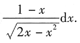
[解析] 求函数的微分常用的方法有两种:一种是先求出了,,再写出如dy=y'dx;另一种方法就是对等式两边直接求微分.读者应选择自己熟悉的方法解题.
3. 设y=1+cos2x,则y'=______
-2 sin 2x.
[解析] 用复合函数求导公式计算即可.
y'=-sin 2x•(2x)'=-2sin2x.
4.
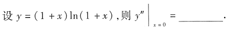
1.
[解析] 先求y',再求y",然后将x=0代入y"即可.
因为

所以
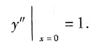
5. 若x=0是函数y=sinx-ax的一个极值点,则a=______
1.
[[分析] 本题考查的知识点是极值的必要条件:若x
0是f(x)的极值点,且f(x)在x
0处可导,
则必有f'(x
0)=0.
因此有
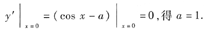
6.
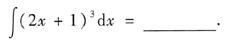
答
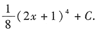
[解析] 凑微分后用积分公式.
7.
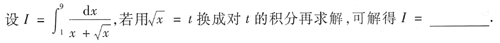
2ln 2.
[[分析] 本题考查的知识点是定积分的换元积分法.换元时,积分的上、下限一定要一起换.

8.
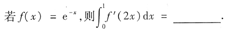
答

[[分析] 本题考查的知识点是积分变量的概念、定积分的性质及定积分的计算.
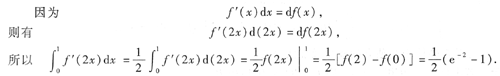
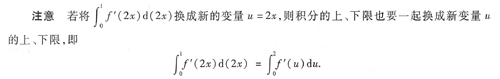
本题也可求出f'(x)=-e
-x,则f'(2x)=-e
-2x,再代人所求式子中,有
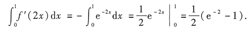
9.

[解析] z对x求偏导时应视丁为常数,并用一元函数求导公式计算.
10.
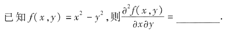
0.
[[分析] 本题考查的知识点是二元函数的二阶偏导数的求法.
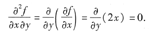
三、解答题1.
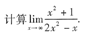
本题考查的知识点是
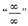
型不定式极限的求法.
[解析]
型不定式极限的一般求法是提取分子与分母中的最高次因子,也可用洛必达法
则求解
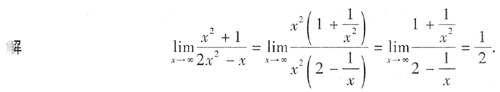
2. 设y=x
2•e
x,求y'.
本题考查的知识点是函数乘积的导数计算.

3.

本题考查的知识点是凑微分积分法.
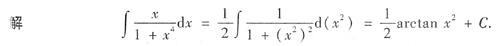
4.
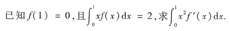
本题考查的知识点是微分的概念、定积分的分部积分法.
[解析] 本题的关键是利用微分的概念将f'(x)dx写成df(x),然后再分部积分,利用已知条考生一定要注意:如果被积函数是x
kf'(x)或x
kf"(x)(k≥1)的形式,应优先考虑用分部积分法 例如:设f(x)的一个原函数是
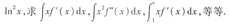
解 因为 f'(x)dx=df(x),
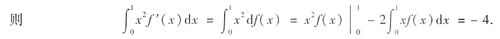
5. 设事件A与B相互独立,且P(A)=0.6,P(B)=0.7,求P(A+B).
本题考查事件相互独立的概念及加法公式.
[解析] 若事件A与B相互独立,则P(AB)=P(A)P(B).
6. 已知函数f(x)=ax
3+bx
2+cx在点x
0处取得极大值5,其导函数y=f'(x)的图像经过点(1,0)和(2,0)(如图1-1所示).
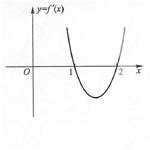
(1)求极值点x
0的值;
(2)求a,b,c的值.
本题考查的知识点是利用导数的图像来判定函数的单调区间和极值点,并以此确定函数的表达式.编者希望通过本题达到培养考生数形结合的能力.
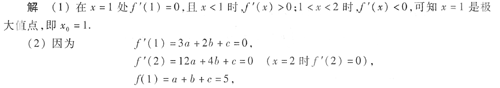
由上面三式解得a=2,b=-9,c=12.
7. 设z=z(x,y)由方程e
z-xy
2+sin(y+z)=0确定,求dz,
本题考查的知识点是二元隐函数全微分的求法.
[解析] 求二元隐函数全微分的关键是先求出偏导数
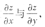
然后代入公式

在用直接求导法时考生一定要注意:等式e
z-xy
2+sin(y+z)=0中的z是x,y的函数,对x (或y)求导时,式子z=z(x,y)中y(或x)应视为常数,最后解出
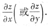
利用公式法求导的关键是需构造辅助函数
F(x,y,z)=e
z-xy
2+sin(y+z),
然后将等式两边分别对x(或y或z)求导.读者一定要注意:对x求导时,y,z均视为常数,而对y或z求导时,另外两个变量同样也视为常数.也即用公式法时,辅助函数F(x,y,z)中的三个变量均视为自变量.
在用公式法时最容易犯的错误是设F(x,y,z)=e
z-xy
2+sin(y+z)=0.如果写成F(x,y,z)

此时的z不是自变量而是z=z(x,y).
根据辅助函数F(x,y,z,),用复合函数求偏导而得到公式

是将x,y视为常数时F(x,y,z)对,的偏导数.
求全微分的第三种解法是直接对等式两边求微分,最后解出dz,这种方法也十分简捷有效,
建议考生能熟练掌握.
解法一 等式两边对x求导得

等式两边对y求导得

解法二
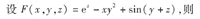

解法三
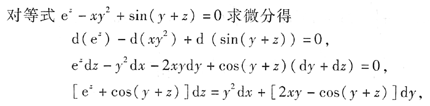
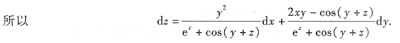
8. 求由曲线y=2-x
2,y=2x-1及x≥0围成的平面图形的面积S以及此平面图形绕x轴旋转一周所得旋转体的体积V
x.
本题考查的知识点有平面图形面积的计算及旋转体体积的计算.
[解析] 本题的难点是根据所给的已知曲线画出封闭的平面图形,然后再求其面积S.求面积的关键是确定对x积分还是对y积分.
确定平面图形的最简单方法是:题中给的曲线是三条,则该平面图形的边界也必须是三条,多一条或少一条都不是题中所要求的.
确定对x积分还是对丁积分的一般原则是:尽可能用一个定积分而不是几个定积分之和来表示,本题如改为对y积分,则有
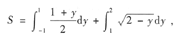
计算量显然比对x积分的计算量要大,所以选择积分变量的次序是能否快而准地求出积分的关键
在求旋转体的体积时,一定要注意题目中的旋转轴是x轴还是y轴.由于本题在x轴下面的图形绕x轴旋转成的体积与x轴上面的图形绕x轴旋转的旋转体的体积重合了,所以只要计算x轴上面的图形绕x轴旋转的旋转体体积即可.如果将旋转体的体积写成
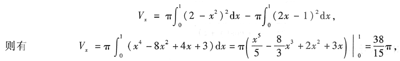
两者之差

恰为x轴下面有三角形图形绕x轴旋转一周的旋转体体积

上面的这种错误是考生比较容易出现的,所以审题时一定要注意:
解 由已知曲线画出平面图形如图1-2所示的阴影区域.
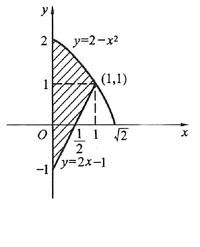
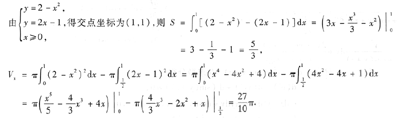
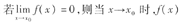 为无穷小量,因此可根据定义计算其极限值,知选C
为无穷小量,因此可根据定义计算其极限值,知选C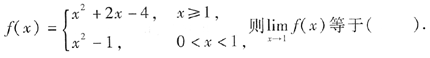
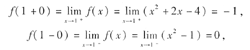
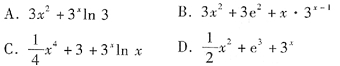
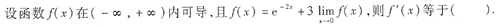

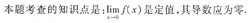
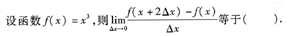


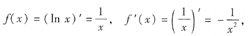
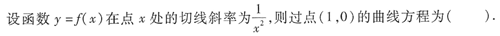


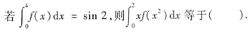

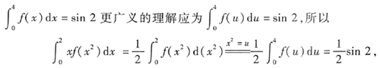
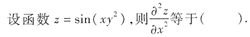
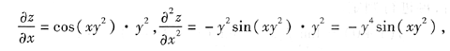

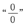 ”型,所以直接利用极限的四则运算法则计算即可.但当x→1时,本题是“
”型,所以直接利用极限的四则运算法则计算即可.但当x→1时,本题是“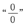 ”型,可用因式分解消去零因式等方法求解.
”型,可用因式分解消去零因式等方法求解.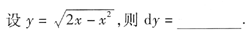
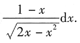
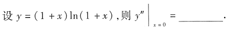

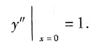
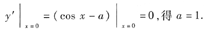
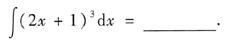
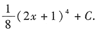
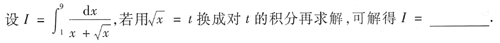

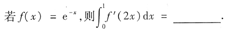

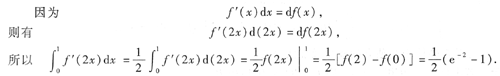
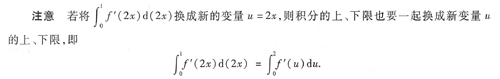
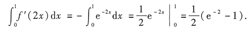


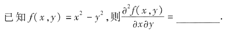
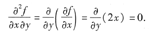
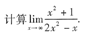
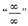 型不定式极限的求法.
型不定式极限的求法. 型不定式极限的一般求法是提取分子与分母中的最高次因子,也可用洛必达法
型不定式极限的一般求法是提取分子与分母中的最高次因子,也可用洛必达法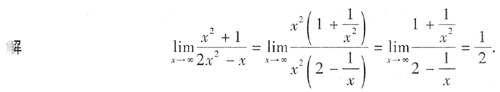


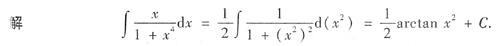
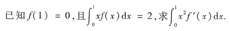
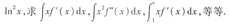
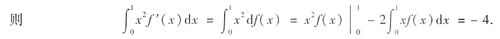

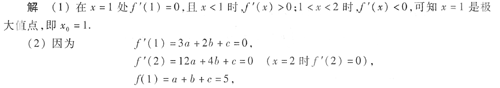
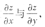 然后代入公式
然后代入公式
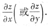

 是将x,y视为常数时F(x,y,z)对,的偏导数.
是将x,y视为常数时F(x,y,z)对,的偏导数.

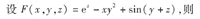

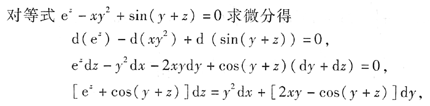
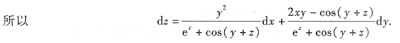
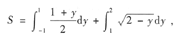
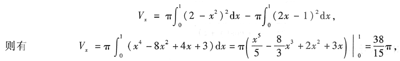
 恰为x轴下面有三角形图形绕x轴旋转一周的旋转体体积
恰为x轴下面有三角形图形绕x轴旋转一周的旋转体体积