一、填空题1. 设n阶矩阵
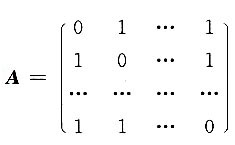
,则|A|=______.
(n-1)(-1)n-1
[解]
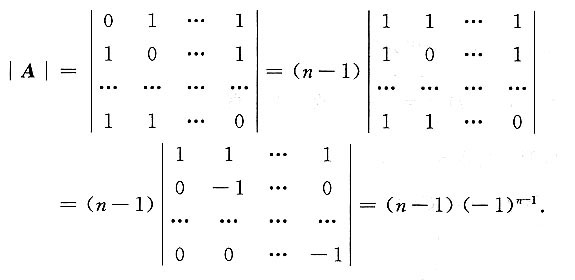
2.
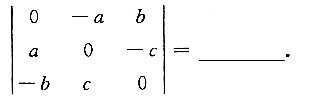
0
[解]
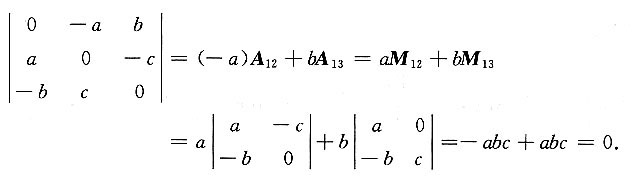
3. 设A,B均为n阶方阵,|A|=2,|B|=-3,则|A
-1B
*-A
*B
-1|=______.
[解] A
*=|A|A
-1=2A
-1,B
*=|B|B
-1=-3B
-1,则
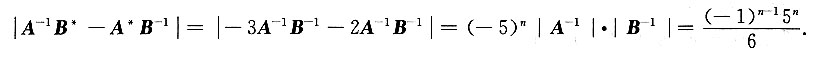
4. 设三阶方阵A=[A
1,A
2,A
3],其中A
i(i=1,2,3)为三维列向量,且A的行列式|A|=-2,则行列式|-A
1~2A
2,2A
2+3A
3,-3A
3+2A
1|=______.
12
[解] 由
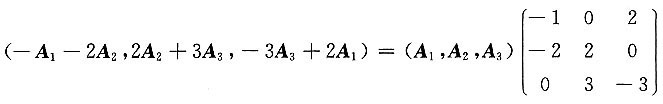
得
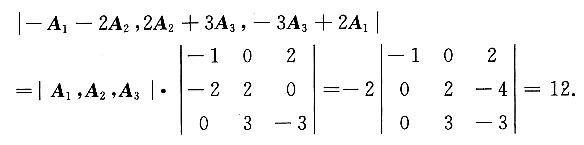
5. 设A是三阶方阵,且|A-E|=|A+2E|=|2A+3E|=0,则|2A
*-3E|=______.
126
[解] 由|A-E|=|A+2E|=|2A+3E|=0得
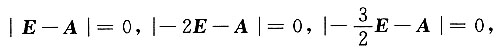
矩阵A的特征值为
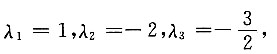
|A|=3,A
*的特征值为
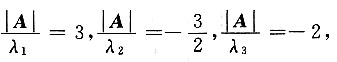
2A
*-3E的特征值为3,-6,-7,故|2A
*-3E|=126.
6. 设A为四阶可逆方阵,将A第3列乘3倍再与第1列交换位置,得到矩阵B,则B
-1A=______.
[解] 由

得
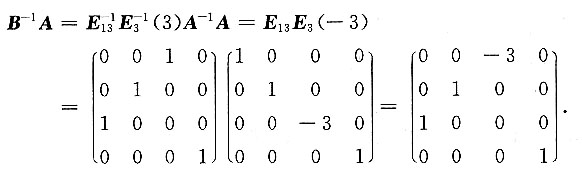
7. 设A为4×3矩阵,且r(A)=2,而
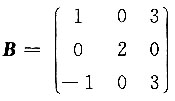
,则r(AB)=______.
2
[解] 因为
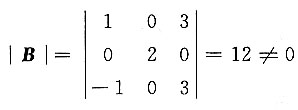
,所以B可逆,
于是r(AB)=r(A)=2.
8. 向量组α
1=[0,4,2-k],α
2=[2,3-k,1],α
3=[1-k,2,3]线性相关,则实数k=______.
6
[解] 由
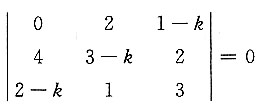
得k=6.
9. 设三阶矩阵
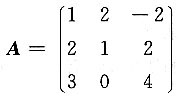
,三维列向量α=(a,1,1)
T.已知Aα与α线性相关,则a=______.
-1
[解] 因为Aα与α线性相关,所以Aα与α成比例,
令Aα=kα,即

10. 设向量组
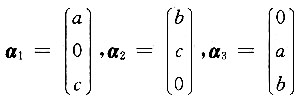
线性无关,则a,b,c必满足关系式______.
abc≠0
[解] 由
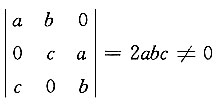
得a,b,c满足的关系式为abc≠0.
11. 若线性方程组
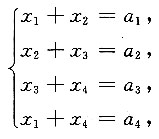
有解,则常数a
1,a
2,a
3,a
4应满足条件______.
a4-a1+a2-a3
[解]

则方程组有解应满足的条件为a
4-a
1+a
2-a
3=0.
12. 若矩阵
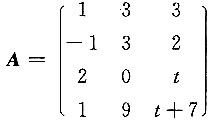
,B是三阶非零矩阵,满足AB=O,则t=______.
1
[解] 由AB=O得r(A)+r(B)≤3,
因为r(B)≥1,所以r(A)≤2,
又因为矩阵A有两行不成比例,所以r(A)≥2,于是r(A)=2.
由
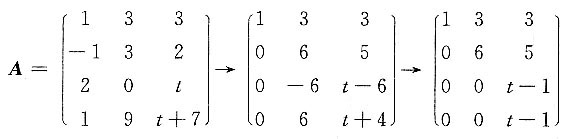
得t=1.
13. 设三阶矩阵A的特征值为2,3,λ,若行列式|2A|=-48,则λ=______.
-1
[解] |A|=6λ,由|2A|=8|A|=-48得|A|=-6,解得λ=-1.
14. 矩阵
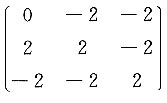
的非零特征值是α
3.
4
[解] 由
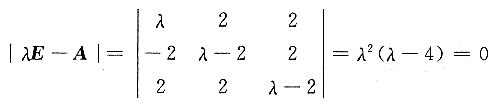
得A的特征值为λ
1=λ
2=0,λ
3=4,非零特征值为4.
15. 已知
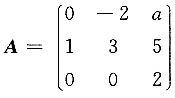
有三个线性无关的特征向量,则a=______.
-10
[解] 由
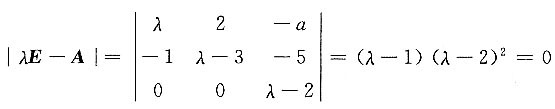
得λ
1=1,λ
2=λ
3=2,
因为A可对角化,所以r(2E-A)=1,
由
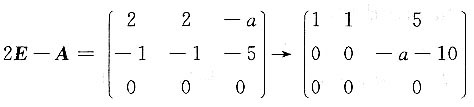
得a=-10.
16. 若
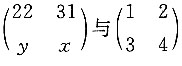
相似,则x=______,y=______.
x=-17,-12
[解] 设
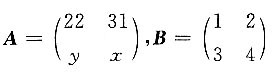
由A与B相似得tr(A)=tr(B),即x+22=5,解得x=-17;
由|A|=|B|得-374-31y=-2,解得y=-12.
17. 已知矩阵
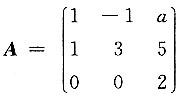
只有两个线性无关的特征向量,则A的三个特征值是______,a=______.
λ1=λ2=λ3=2,a=-5
[解]
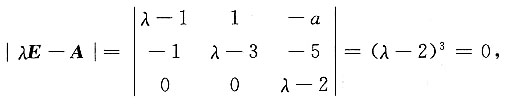
特征值为λ
1=λ
2=λ
3=2,
因为λ
1=λ
2=λ
3=2只有两个线性无关的特征向量,
所以r(2E-A)=1,
由
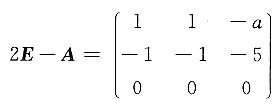
得a=-5.
二、选择题5. 设向量组(Ⅰ):α
1,α
2,…,α
r可由向量组(Ⅱ):β
1,β
2,…,β
s线性表示,则______.
- A.若α1,α2,…,αr线性无关,则r≤s
- B.若α1,α2,…,αr线性相关,则r≤s
- C.若β1,β2,…,βs线性无关,则r≤s
- D.若β1,β2,…,βs线性相关,则r≤s
A B C D
A
[解] 因为(Ⅰ)可由(Ⅱ),所以(Ⅰ)的秩≤(Ⅱ)的秩,
所以若α1,α2,…,αr线性无关,即(Ⅰ)的秩=r,则r≤(Ⅱ)的秩≤s,应选A.
7. 非齐次线性方程组AX=b中未知量个数为n,方程个数为m,系数矩阵A的秩为r,则______.
- A.r=m时,方程组AX=b有解
- B.r=n时,方程组AX=b有唯一解
- C.m=n时,方程组AX=b有唯一解
- D.r<n时,方程组AX=b有无穷多解
A B C D
A
[解] r(
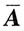
)≥r(A),
当r=m时,r(
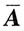
)≥r(A)=m;
又r(
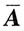
)≤m,所以r(
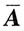
)=r(A)=m,故AX=b有解,应选A.
11. 设矩阵A
m×n,r(A)=m<n,E
m为m阶单位矩阵,下述结论中正确的是______.
- A.A通过初等行变换必可化为[Em,0]的形式
- B.A的任意m阶子式不等于零
- C.A的任意m个列向量必线性无关
- D.非齐次线性方程组AX=b一定有无穷多解
A B C D
D
[解] 显然
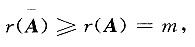
因为
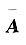
为m×(n+1)矩阵,所以
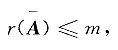
于是
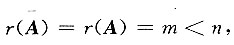
故AX=b一定有无数个解,应选D.
13. 设
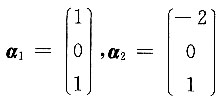
都是线性方程组AX=0的解向量,只要系数矩阵A为______.
A.
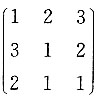
B.

C.
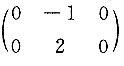
D.

A B C D
C
[解] 因为α
1,α
2线性无关,所以AX=0的基础解系至少含两个线性无关的解向量,从而r(A)≤1,
再由题意得
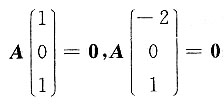
,显然选C.
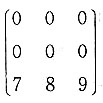
15. 下列矩阵中,不能相似对角化的是______.
A.

B.
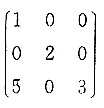
C.
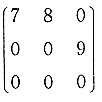
D.
A B C D
C
[解]
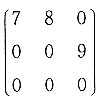
的特征值为7,0,0,因为r(0E-A)=r(A)=2,所以λ=0对应的线性无关的特征向量只有一个,该矩阵不可相似对角化,应选C.
 ,则|A|=______.
,则|A|=______.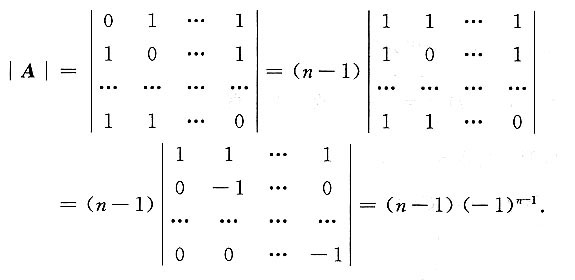
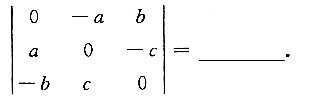
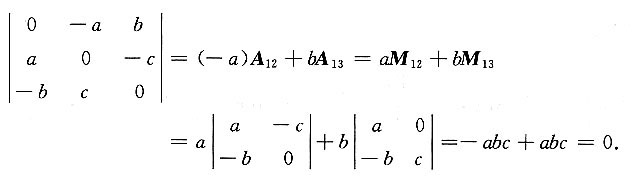
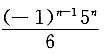
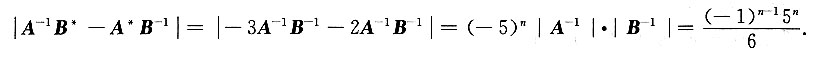
 得
得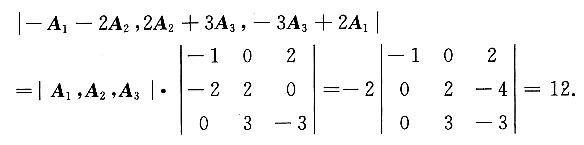
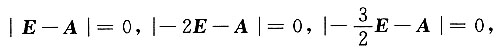
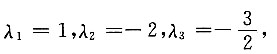
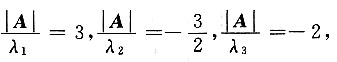

 得
得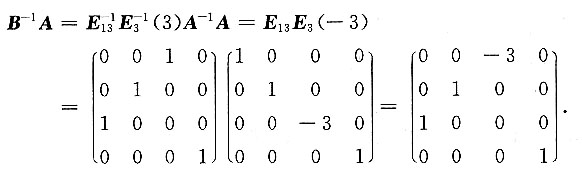
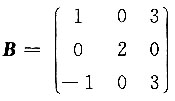 ,则r(AB)=______.
,则r(AB)=______. ,所以B可逆,
,所以B可逆,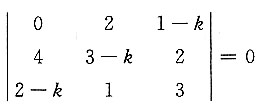 得k=6.
得k=6.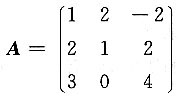 ,三维列向量α=(a,1,1)T.已知Aα与α线性相关,则a=______.
,三维列向量α=(a,1,1)T.已知Aα与α线性相关,则a=______.
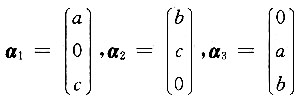 线性无关,则a,b,c必满足关系式______.
线性无关,则a,b,c必满足关系式______.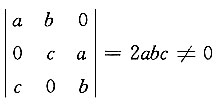 得a,b,c满足的关系式为abc≠0.
得a,b,c满足的关系式为abc≠0.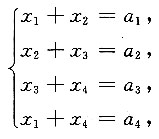 有解,则常数a1,a2,a3,a4应满足条件______.
有解,则常数a1,a2,a3,a4应满足条件______.
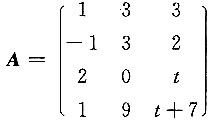 ,B是三阶非零矩阵,满足AB=O,则t=______.
,B是三阶非零矩阵,满足AB=O,则t=______. 得t=1.
得t=1.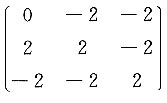 的非零特征值是α3.
的非零特征值是α3.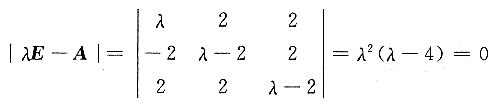 得A的特征值为λ1=λ2=0,λ3=4,非零特征值为4.
得A的特征值为λ1=λ2=0,λ3=4,非零特征值为4.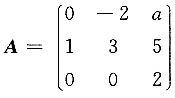 有三个线性无关的特征向量,则a=______.
有三个线性无关的特征向量,则a=______.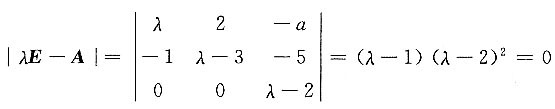 得λ1=1,λ2=λ3=2,
得λ1=1,λ2=λ3=2,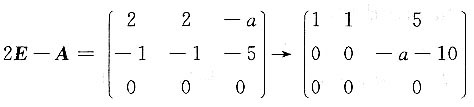 得a=-10.
得a=-10.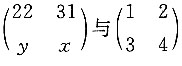 相似,则x=______,y=______.
相似,则x=______,y=______.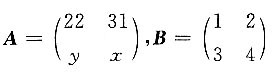
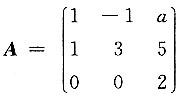 只有两个线性无关的特征向量,则A的三个特征值是______,a=______.
只有两个线性无关的特征向量,则A的三个特征值是______,a=______.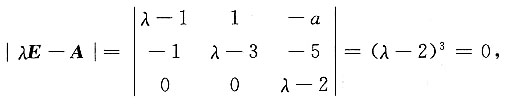
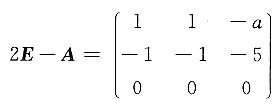 得a=-5.
得a=-5. )≥r(A),
)≥r(A), )≥r(A)=m;
)≥r(A)=m;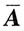 )≤m,所以r(
)≤m,所以r(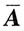 )=r(A)=m,故AX=b有解,应选A.
)=r(A)=m,故AX=b有解,应选A.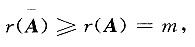
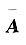 为m×(n+1)矩阵,所以
为m×(n+1)矩阵,所以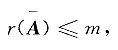
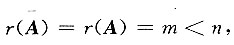 故AX=b一定有无数个解,应选D.
故AX=b一定有无数个解,应选D. ,若齐次方程组AX=0的任一非零解均可用α线性表示,则a=______.
,若齐次方程组AX=0的任一非零解均可用α线性表示,则a=______.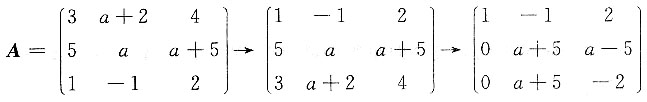 得a-5=-2,解得a=3,应选A.
得a-5=-2,解得a=3,应选A.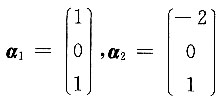 都是线性方程组AX=0的解向量,只要系数矩阵A为______.
都是线性方程组AX=0的解向量,只要系数矩阵A为______.

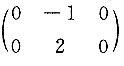

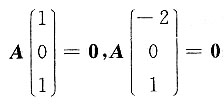 ,显然选C.
,显然选C.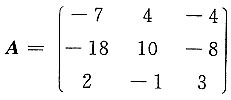 ,则______不是A的特征向量.
,则______不是A的特征向量.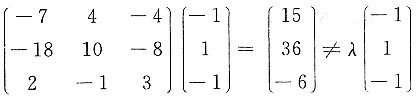 得
得 不是A的特征向量,应选A.
不是A的特征向量,应选A.



 的特征值为7,0,0,因为r(0E-A)=r(A)=2,所以λ=0对应的线性无关的特征向量只有一个,该矩阵不可相似对角化,应选C.
的特征值为7,0,0,因为r(0E-A)=r(A)=2,所以λ=0对应的线性无关的特征向量只有一个,该矩阵不可相似对角化,应选C. ,则A与B______.
,则A与B______.