一、选择题在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内 二、填空题把答案填在题中横线上1.
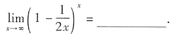
[解析] 本题考查对重要极限Ⅱ的理解和掌握.根据重要极限Ⅱ的结构式可知该极限值为
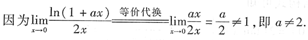
2.
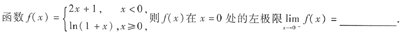
1.
[解析] 利用左极限的定义即可知:
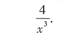
3. 设函数y=sin(lnx),则y'=______
4. 设函数f(x)=cos[ln(x+1)],则f'(x)=______
[解析] 本题考查复合函数的求导.
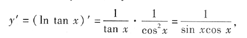
5. 设函数y=x
10x
10+e
x,则y
(100)=______
ex.
[解析] 本题考查的知识点是高阶导数的概念及计算.由于(x10)(10)=10!,则(x10)(100)=0,而 (ex)(n)=ex.所以填ex.
6. 曲线y=x
3(上标)+3x2(上标)+1的拐点坐标为______
(-1,3).
[解析] 本题考查拐点的概念及其求法.由于
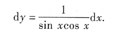
y"<0;x>-1时,y">0,所以x=-1,y=3为曲线的拐点.故填(-1,3).由于拐点是曲线上的点,不能填x=-1,请考生务必注意.
7.
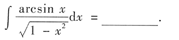
8.
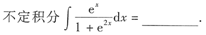
9.
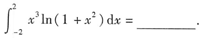
0.
[解析] 本题考查奇(或偶)函数在对称区间积分的性质.由于被积函数为奇函数,所以在 [-2,2]上的定积分值为0.
10. 设函数z=ln(1+xy),则dz=______
[解析] 对x(或y)求导时,y(或x)应视为常数.用一元函数求导公式求出
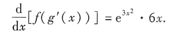
代入dz即可.
三、解答题解答应写出推理、演算步骤1.
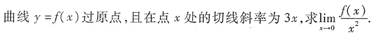
本题考查的知识点是
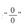
型不定式极限的求法及导数几何意义的应用.
[解析] 求
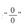
型不定式极限的常用方法是等价无穷小量代换或洛必达法则.
请读者注意,已知条件中的y=f(x)过原点即f(0)=0,所以原式的极限是
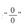
型.
解 因为f(0)=0,所以
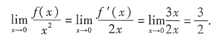
2.
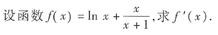
本题考查的知识点是基本初等函数的求导计算.
[解析] 直接用公式计算.
解
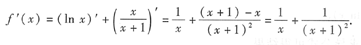
注意 由于
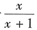
是假分式,化为整式+真分式后再求导更简单,即
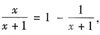
则
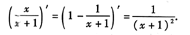
3.
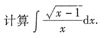
4.
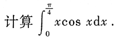
本题考查的知识点是定积分的分部积分法.
解
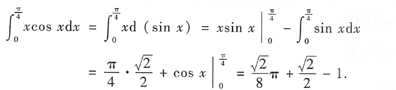
5. 设随机变量X的分布列为
X | -1 | 0 | 1 | 2 |
P | 0.1 | 0.3 | 0.2 | 0.4 |
求EX和DX.
解 EX=(-1)×0.1+0×0.3+1×0.2+2×0.4=0.9.
DX=(-1-0.9)2×0.1+(0-0.9)2×0.3+(1-0.9)2×6.2+(2-0.9)2×0.4=1.09.
6. 求曲线y=e
x和y=x,x=1,y轴所围成的平面图形的面积S;
(2)求(1)中的平面图形绕x轴旋转一周所成旋转体的体积V
x.
解 画出平面区域,如图9-3所示的阴影区域.
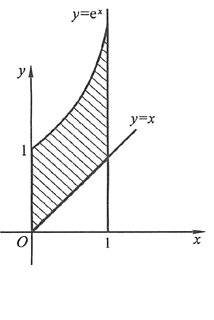
(1)
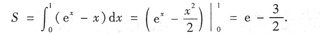
(2)
7. 建一比赛场地面积为Sm
2的排球场馆,比赛场地四周要留下通道,南北各留出am,东西各留出bm,如图9-2所示.求铺设的木地板的面积为最少时(要求比赛场地和通道均铺设木地板),排球场馆的长和宽各为多少m?
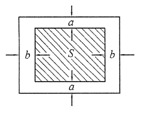
解 设排球场馆的长和宽分别为x和y,其面积为A=xy.如图9-4所示.
比赛场地的面积为S=(x-2b)(y-2a),则
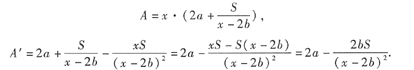
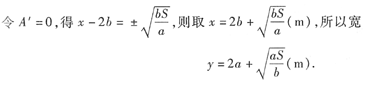
由于只有唯一驻点,根据题意可知长为
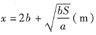
,宽为
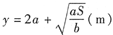
时的场馆面积为最小(即所铺地用的木地板面积为最少).
8. 求函数z=3xy-x
3-y
3的极值.
令
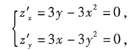
求出驻点(0,0),(1,1).
因为
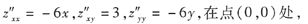
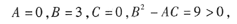
故(0,0)为非极值点.
在点(1,1)处,
A=-6,B=3,c=0,B
2-AC=9>0
故点(1,1)为极大值点.极大值为z(1,1)=1.