一、选择题在每小题给出的四个选项中,只有—项是符合题目要求的,把所选项前的字母填在题后的括号内 三、解答题解答应写出推理、演算步骤1.
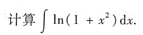
本题考查的知识点是“0·∞”型不定式极限的求法.
[解析] 计算“0·∞”型不定式的极限,必须将它化为
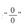
型或
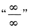
型不定式,再用洛必达法则或其他方法求解.
将“0·∞”型不定式变形为
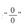
型还是
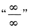
型不定式,无必然的规律可言.但是一个基本原则是:变形后,在用洛必达法则时,应使其分子或分母的导数简单易求,而且求导后的极限应该比求导前的
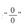
型或
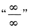
型不定式的极限简单.
解法一
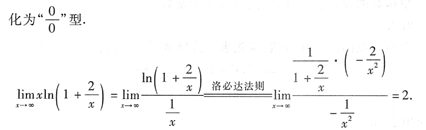
解法二
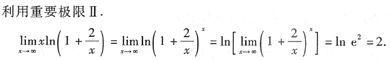
解法三
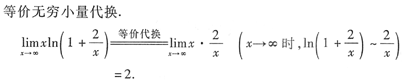
三种不同的解法中,等价无穷小量代换最为简捷.灵活地掌握各种不同的解题方法定能极大地提高考生的解题能力.
2.
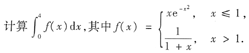
本题考查的知识点是复合函数的求导.
解
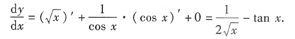
3.
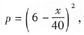
本题考查的知识点是用凑微分法积分.
解
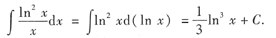
4.
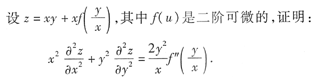
本题考查的知识点是绝对值函数的定积分,其关键是去掉绝对值符号.方法是:令
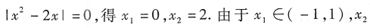
在区间(-1,1)外面,所以应分成两段积分.
解
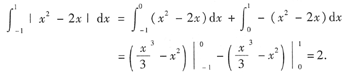
5. 设随机变量父的分布列为
X | -1 | 0 | 1 | 2 | 3 |
P | 0.2 | 0.1 | 0.3 | a | 0.3 |
(1)求常数a;
(2)求X的分布函数F(x),并画出F(x)的图像.
本题考查的知识点是概率分布规范性的性质及分布函数的求法.
解 (1)由概率分布的规范性可知
0.2+0.1+0.3+0+0.3=1,得a=0.1.
(2)当x<-1时,F(x)=0;
当-1≤x<0时,F(x)=0.2;
当0≤x<1时,F(x)=0.3;
当1≤x<2时,F(x)=0.6;
当2≤x<3时,F(x)=0.7;
当x≥3时,F(x)=1,
所以
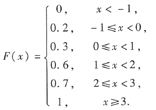
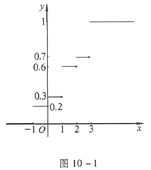
F(x)的图像如图10-1所示.
6. 设函数f(x)=x
3-3ax
2+3bx的图像与直线12x+y-1=0相切于点 (1,-11),求:
(1)a,b的值;
(2)f(x)的单调区间.
本题考查的知识点是导数的应用及函数的单调区间的求法.
解 (1)由于f(x)的图像与直线12x+y-1=0相切于点(1,-11),所以
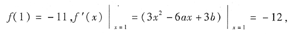
即

(2)
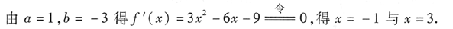
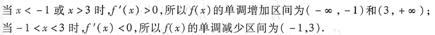
7.
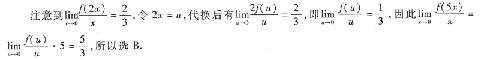
本题考查的知识点是隐函数求偏导.隐函数求偏导常用的有两种方法:公式法和微法.直接求导的方法计算量比较大,建议考生熟练掌握公式法.

解
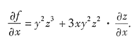
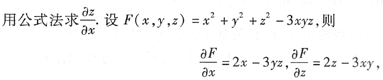
所以
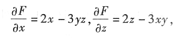
因此有
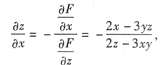
所以
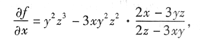
也可用微分法求
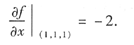
对等式x
2+y
2+z
2-3xyz=0求微分,得
2xdz+2ydy+2zdz-3yzdx-3xzdy-3xydz=0,
解得
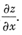
比较
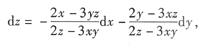
8.
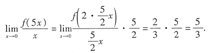
本题考查利用定积分的有关知识
[解析] 问题的能力.