一、选择题2. 设
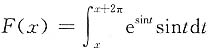
,则F(x)______.
A B C D
A
[解析] 由周期函数的平移性质,
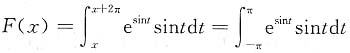
,再由对称区间积分性质得
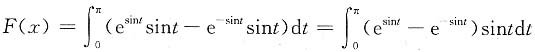
,
又(e
sint-e
-sint)sint连续、非负、不恒为零,所以F(x)>0,选A.
5. 设f(x)在R上是以T为周期的连续奇函数,则下列函数中不是周期函数的是______.
A.
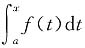
B.
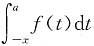
C.
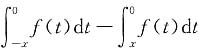
D.
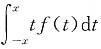
A B C D
D
[解析] 设

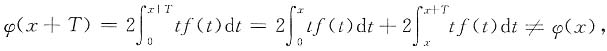
选D.
6. 设函数f(x)连续,下列变上限积分函数中,必为偶函数的是______.
A.
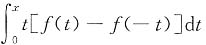
B.
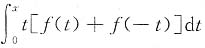
C.
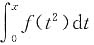
D.
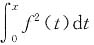
A B C D
B
[解析] 因为t[f(t)-f(-t)]为偶函数,所以
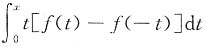
为奇函数,A不对;因为f(t
2)为偶函数,所以
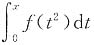
为奇函数,C不对;因为不确定f
2(t)的奇偶性,所以D不对;令
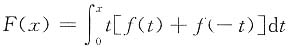
,
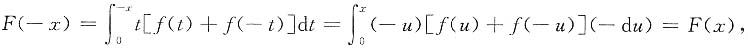
选(B).
7. 若由曲线
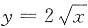
,曲线上某点处的切线以及x=1,x=3围成的平面区域的面积最小,则该切线是______.
A.
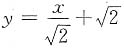
B.
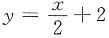
C.y=x+1
D.
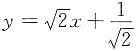
A B C D
A
[解析] 计算下列不定积分:
曲线
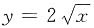
在点
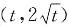
处的切线方程为
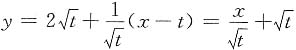
,由于切线位于曲线
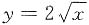
的上方,所以由曲线
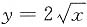
,切线及x=1,x=3围成的面积为
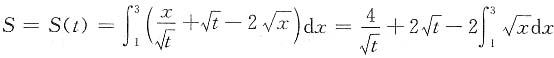
.
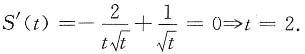
当t∈(0,2)时,S'(t)<0;当t∈(2,3)时,S'(t)>0,则当t=2时,S(t)取最小值,此时切线方程为
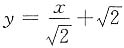
,选A.
二、解答题1. 设f(x)连续,且
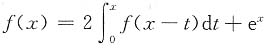
,求f(x).
解
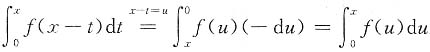
,
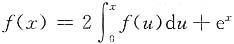
两边求导数得f'(x)-2f(x)=e
x,
则f(x)=(∫e
x·e
∫-2dxdx+C)e
-∫-2dx=Ce
2x-e
x,
因为f(0)=1,所以C=2,故f(x)=2e
2x-e
x.
2.
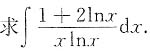
解
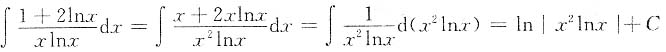
3.
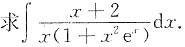
解 因为(x
2e
x)'=(x
2+2x)e
x,
所以
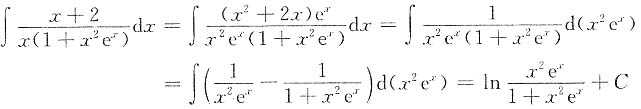
5. 设F(x)为f(x)的原函数,且当x≥0时,
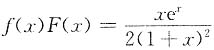
,又F(0)=1,F(x)>0,求f(x).
解 两边积分得
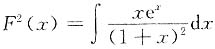
,解得
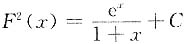
,由F(0)=1,F(x)>0,得
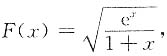
于是
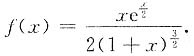
6. 设
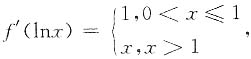
求f(x).
解 令lnx=t,则
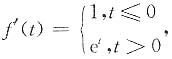
当t≤0时,f(t)=t+C
1;当t>0时,f(t)=e'+C
2.
显然f'(t)为连续函数,所以f(t)也连续,于是有C
1=1+C
2,故f(x)=

7.

8. 设f(x)连续,
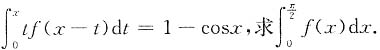
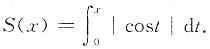
9. 证明:当nπ≤x<(n+1)π时,2n≤S(x)<2(n+1);
证明 当nπ≤x<(n+1)π时,
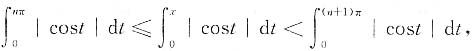
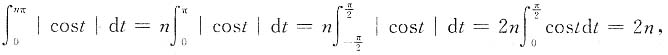
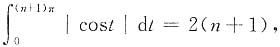
则2n≤S(x)<2(n+1).
10.
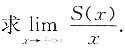
解 由nπ≤x<(n+1)π,得
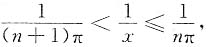
从而
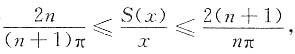
根据夹逼定理得
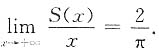
11. 设f(x)在[0,+∞)上连续,非负.且以T为周期,证明:
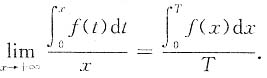
证明 对充分大的x,存在自然数n,使得nT≤x<(n+1)T,
因为f(x)≥0,所以
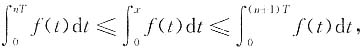
即
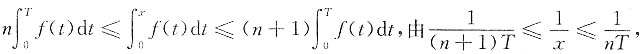
得

注意到当x→+∞时,n→+∞,且
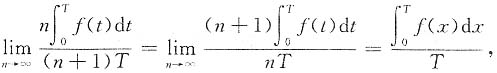
由夹逼定理得
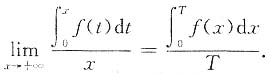
12. 设f(x)在[0,1]上连续,f(0)=0,
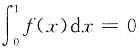
.证明:存在ξ∈(0,1),使得
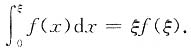
证明 令

因为f(x)在[0,1]上连续,所以φ(x)在[0,1]上连续,在(0,1)内可导,又φ(0)=0,
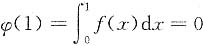
,由罗尔定理,存在ξ∈(0,1),使得φ'(ξ)=0,而
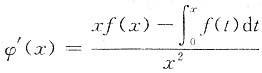
,所以
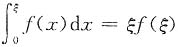
.
13. 证明:对0<x<a,存在0<θ<1,使得
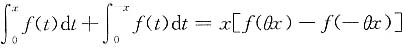
;
证明 令
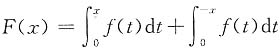
,显然F(x)在[0,x]上可导,且F(0)=0,由微分中值定理,存在0<θ<1,使得F(x)=F(x)=F(0)=F'(θx)x,即
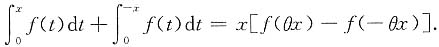
14.
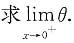
15. 设

,证明:
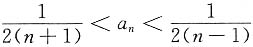
.
证明
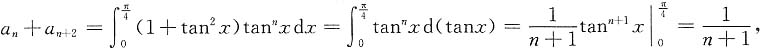
同理
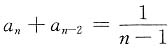
.因为tan
nx,tan
n+2x在
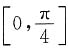
上连续,tan
nx≥tan
n+2x,且tan
nx,tan
n+2x不恒等,所以
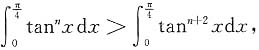
即a
n>a
n+2,
于是
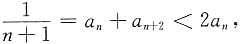
即
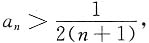
同理可证
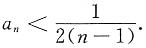
16. 设f(x)有界,且f'(x)连续,对任意的x∈(-∞,+∞)有|f(x)+f'(x)|≤1.证明:|f(x)|≤1.
证明 令φ(x)=e
xf(x),则φ'(x)=e
x[f(x)+f'(x)],
由|f(x)+f'(x)|≤1得|φ'(x)|≤e
x,又由f(x)有界得φ(-∞)=0,则
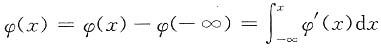
,两边取绝对值得
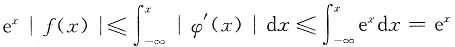
,所以|f(x)|≤1.