一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的)5. 设3元线性方程组Ax=b,已知r(A)=r(A,b)=2,其两个解η
1,η
2满足η
1+η
2=(-1,0,1)
T,η
1-η
2=(-3,2,-1)
T,k为任意常数,则方程组Ax=b的通解为______
A.
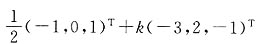
B.
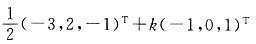
C.(-1,0,1)
T+k(-3,2,-1)
T D.(-3,2,-1)
T+k(-1,0,1)
T A B C D
A
[解析] 由题意可知,
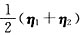
是线性方程组Ax=b的一个解,η
1-η
2是Ax=0的一个基础解系,故方程组Ax=b的通解为
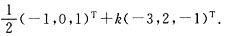
二、填空题1. 设

,则a
0=______.
2. 2阶行列式
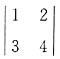
第2行元素的代数余子式之和为______.
3. 已知矩阵A=(1,0,-1),B=(2,-1,1),且C=A
TB,则C
2=______.
[解析]

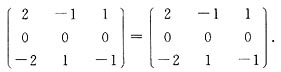
4. 设A为2阶矩阵,若存在矩阵
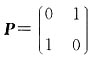
,使得
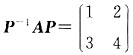
,则A=______.
5. 设向量α
1=(1,1,-1)
T,α
2=(1,-1,1)
T,α
3=(-1,1,1)
T,β=(1,0,0)
T,则β由向量组α
1,α
2,α
3线性表出的表示式为______.
[解析] 因为β可由向量组α
1,α
2,α
3线性表出,故存在不全为0的k
1,k
2,k
3使得
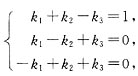
解
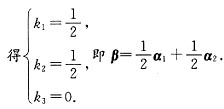
6. 设向量组α
1=(-2,1,3)
T,α
2=(1,0,-1)
T,α
3=(k+2,1,0)
T线性相关,则数k=______.
7. 设向量α
1=(1,-1,2)
T与α
2=(4,0,k)
T正交,则数k=______.
-2
[解析] 因为向量α1与α2正交,所以α1·α2=(α1,α2)=4-1×0+2k=0,k=-2.
8. 设3元非齐次线性方程组Ax=b的增广矩阵
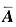
经初等行变换化为
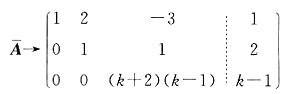
若该方程组有无穷多解,则数k=______.
1
[解析] 若非齐次线性方程组有无穷多解,则

则k=1.
9. 矩阵
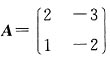
的两个特征值之和等于______.
10. 二次型
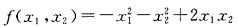
的规范形为______.
三、计算题(每小题9分,共63分)2. 设矩阵
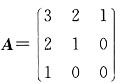
,求A
*及A
-1.
解:由于
A
11=0,A
21=0,A
31=-1,
A
12=0,A
22=-1,A
32=2,
A
13=-1,A
23=2,A
33=-1,
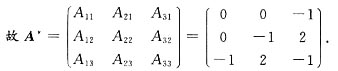
又

,则A可逆,
且
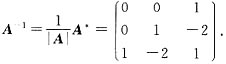
3. 设A为3阶矩阵,将A第1行的2倍加到第3行得到矩阵B,再将B第2列与第3列互换得到单位矩阵E,求矩阵A.
解:由题设可知,存在初等矩阵
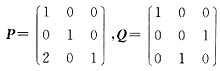
使得PA=B,BQ=E,即PAQ=E,
所以A=P
-1EQ
-1=P
-1Q
-1 
4. 求向量组α
1=(1,2,3,-1)
T,α
2=(2,3,4,-3)
T,α
3=(0,0,1,2)
T,α
4=(3,4,3,-9)
T,α
5-(1,1,2,0)
T的秩和一个极大线性无关组,并将向量组中的其余向量由该极大线性无关组线性表出.
解:
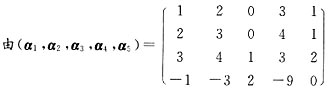

可知向量组的秩为3,α
1,α
2,
3α3为一个极大线性无关组,并且有
α
4=-α
1+2α
2-2α
3,α
5=-α
1+α
2+α
3.
(答案不唯一)
5. 求线性方程组
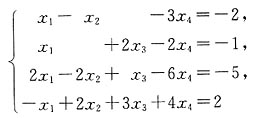
的通解(要求用其一个特解和导出组的基础解系表示).
解:对方程组的增广矩阵进行初等行变换
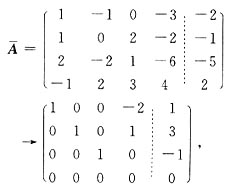
得同解方程组
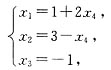
从而方程组的通解为
x=(1,3,-1,0)
T+k(2,-1,0,1)
T(k为任意常数).
6. 设A为3阶实对称矩阵,已知r(A)=2,α1=(1,0,-1)
T,α
2=(1,0,1)
T分别是A的属于特征值λ
1=-1,λ
2=1的特征向量.求A的另一个特征值和对应的特征向量.
解:设λ
3为A的另一个特征值,α
3是A的属于特征值λ
3的特征向量.
由于r(A)=2,故|A|=λ
1λ
2λ
3=0,
而λ
1=-1,λ
2=1,因此λ
3=0.
又A为3阶实对称矩阵,故α
3与α
1,α
2都正交,
令α
3=(x
1,x
2,x
3)
T,则口α
1Tα
3=0,
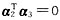
,即
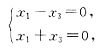
得基础解系(0,1,0)
T,
所以A的属于特征值λ
3=0的全部特征向量为
k(0,1,0)
T,k为非零常数.
7. 求正交变换x=Qy,将二次型
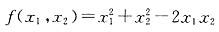
化为标准形.
解:二次型的矩阵
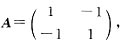
由
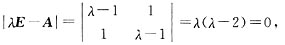
得A的特征值λ
1=2,λ
22=0.
对于λ
1=2,求解齐次线性方程组(2E-A)x=0,得基础解系
α
3=(-1,1)
T,
单位化得
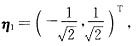
对于λ
2=0,求解齐次线性方程组(-A)x=0,得基础解系
α
1=(1,1)
T,
单位化得
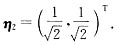
令
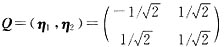
,则Q位正交矩阵,
从而经正交变换
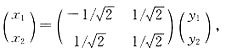
将二次型化为标准形
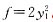
.