第Ⅰ部分 选择题
一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)5. 系统的静态加速度误差系数K
a的定义式为______
A.
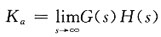
B.
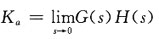
C.
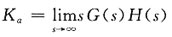
D.
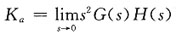
A B C D
D
[考点] 本题主要考查的知识点为系统静态加速度误差系数的定义式。
[解析] 系统静态加速度误差系数的定义式为
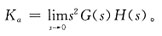
7. 系统
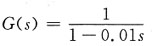
的奈奎斯特图为______
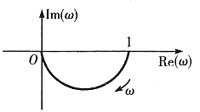
A.
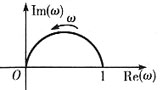
B.
C.

D.
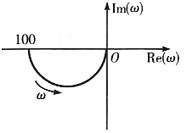
A B C D
B
[考点] 本题主要考查的知识点为非最小相位系统奈奎斯特图的画法。
[解析] 由于
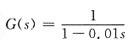
和G(s)=

的幅频特性相同(即G(jω)的实部相同),相频特性(即G(jω)的虚部)的符号相反。又由惯性环节的奈奎斯特图可知,本题应选B。
8. 已知某机械系统的传递函数为
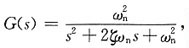
则系统的阻尼自然频率ω
d为______
A.
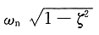
B.
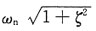
C.
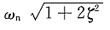
D.
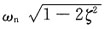
A B C D
A
[考点] 本题主要考查的知识点为阻尼自然频率ω
d和无阻尼自然频率ω
n之间的关系。
[解析] 二阶系统中,ω
d与ω
n之间的关系式为
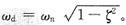
10. 下列串联校正装置的传递函数中,能在频率ω
c=4处提供最大相位超前角的是______
A.
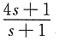
B.
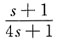
C.
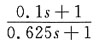
D.

A B C D
D
[考点] 本题主要考查的知识点为串联相位超前校正装置,在最大超前相位处的频率也即几何中点频率与两个转角频率的关系。
[解析] 选项B和C都是串联相位滞后校正装置,产生的是负的相位,选项A的两个转角频率分别为
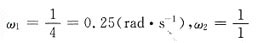
=1(rad·s
-1),故ω
c=4不在二者之间;而选项D的两个转角频率为
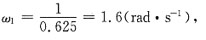
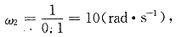
所以ω
c=4介于二者之间,故选D。
第Ⅱ部分 非选择题
二、填空题1. 负反馈指反馈回去的信号与原系统的输入信号相位相差______。
3. 在系统的输出表达式中,与初始条件有关的部分称为系统的补函数,与______有关的部分称为系统的特解函数。
5. 在系统中凡有储存或积累特点的元件,都有______环节的特性。
6. 在时域分析法中,常采用的典型输入信号有______、阶跃函数、斜坡函数和加速度函数等。
7. 已知典型二阶系统的阻尼比为ζ=0.5,则系统的单位阶跃响应呈现为______。
8. 二阶微分环节与振荡环节的对数幅频曲线对称于______。
9. 对最小相位系统而言,若系统是稳定的,则相位裕量γ和幅值裕量K
g都应该______。
10. 按校正环节在原系统中并联的方式,并联校正又可分为反馈校正、______和前馈校正。
三、简答题(本大题共30分)1. 对控制系统的基本要求是什么?
对控制系统的基本要求有系统的稳定性、响应的快速性和响应的准确性等。其中系统的稳定性是系统能够正常工作的首要条件。
2. 机械工程控制论的研究对象和任务是什么?
机械工程控制论是研究以机械工程技术为对象的控制论问题。具体地讲,是研究在这一工程领域中广义系统的动力学问题,也就是研究系统及其输入、输出三者之间的动态关系。
机械工程控制论的研究任务主要分为以下五个方面:
(1)当系统已定,并且输入已知而输出未知时,要求确定系统的输出(响应),并根据输出来分析和研究该控制系统的性能,此类问题称为系统分析。
(2)当系统已定,且系统的输出也已给定而输入未施加时,要确定系统的输入以使输出尽可能符合给定的最佳要求,此类问题称为最优控制。
(3)当输入已知,且输出也是给定,而系统尚未构建时,确定系统应使得输出尽可能符合给定的最佳要求,此类问题即最优设计。
(4)当输入与输出均已知,而系统结构参数未知时,求出系统的结构与参数,即建立系统的数学模型,此类问题即系统辨识。
(5)当系统已定,输出已知而输入已施加但未知时,要求识别输入或输入中的有关信息,此类问题即滤波与预测。
3. 试分析二阶系统在不同阻尼下特征根的形式和位置分布及其对应的阶跃响应曲线的形状。
4. 在频率特性的图形表示方法中,常用的方法有哪几种?
在频率特性的图形表示方法中,常用的方法有如下三种:
(1)对数坐标图或称为伯德图。
(2)极坐标图或称为奈奎斯特图。
(3)对数幅一相图。
5. 系统开环频率特性各频段含义及对系统性能的影响。
一般将系统开环频率特性的幅值穿越频率ω
c看成是频率响应的中心频率,并将在ω
x附近的频率区段称为中频段;把频率
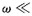
ω
c的频率区段称为低频段;把
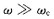
的频率区段称为高频段。三个频段的划分没有严格的界限。
而决定系统稳态特性好坏的主要参数(如开环增益,系统的型次等)可以通过系统的低频段求得;决定系统动态特性好坏的主要参数(如幅值穿越频率、相位裕量等)可以通过系统的中频段求得;系统的抗干扰能力等,则可以由系统的高频段来表示。
故低频段反应了系统的稳态性能;中频段反映了系统的动态性能;高频段反映了系统抵抗高频干扰的能力。
四、分析计算题(本大题共30分)1. 系统的微分方程为
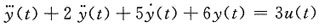
,试求系统的传递函数。
对微分方程在零初始条件下进行拉氏变换:
s
3y(s)+2s
2Y(s)+5sY(s)+6Y(s)=3U(s)
则系统的传递函数为
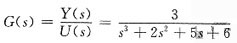
2. 设系统框图如下图所示,试用框图的简化法求
框图简化过程如下所示:
故
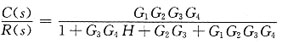
3. 已知单位反馈系统的开环传递函数为
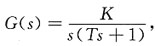
试求参数K的取值范围以满足下面的指标:当输入r(t)=t时,系统的稳态误差e
ss≤0.02。
由开环传递函数知系统为Ⅰ型系统。
当r(t)=t时,系统的稳态误差为
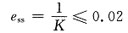
故开环增益应取K≥50。