一、单项选择题1. 设有一组观测数据(x
i,y
i),i=1,2,…,n,其散点图呈线性趋势,若要拟合一元线性回归方程
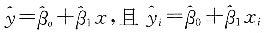
,i=1,2,…,n,则估计参数β
0,β
1应使______
A.
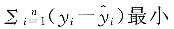
B.
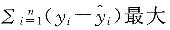
C.
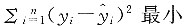
D.
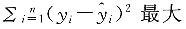
A B C D
C
[解析] 最小二乘法的基本思想是选取β
0,β
1的估计量
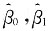
,使

,其中右端min是对一切β
0,β
1的容许值取的Q的最小值.答案为C.
3. 设随机变量ξ和η的密度函数分别为
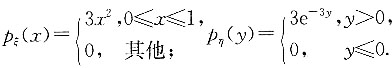
若ξ与η不相关,E(ξη)=
A.
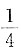
B.
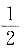
C.
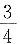
D.1
A B C D
A
[解析]
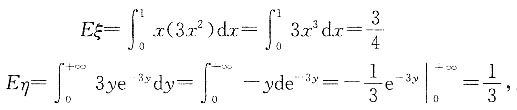
又ξ和η不相关,则
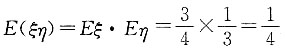
.
6. X服从[1,3]上的均匀分布,下列结论不正确的是______
A.P(X=2)=0.5
B.P(X>2)=0.5
C.E(X)=2
D.
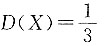
A B C D
A
[解析] 连续型随机变量取一个定值的概率为零,所以A错.根据已知,X的概率密度函数为
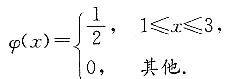
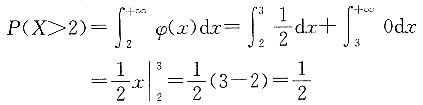
,所以B对.
均匀分布X的期望
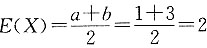
,所以C对.
均匀分布X的方差
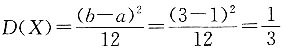
,所以D对.
8. 对线性回归模型y=a+bx+ε,ε~N(0,σ
2),如由一组观测值(x
i,y
i),(i=1,2,…,n)建立的线性回归方程为:
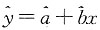
,则______不成立(其中
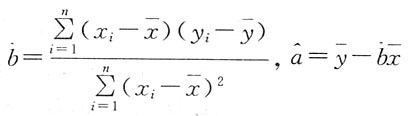
)
A.
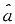
是a的有偏估计
B.
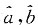
分别是a,b的极大似然估计
C.
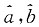
分别是a,b的最小二乘估计
D.
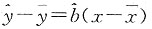
A B C D
A
[解析] 由于
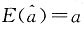
,所以
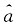
是a的无偏估计,选项A错;
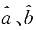
分别是a、b的极大似然估计,选项B对;
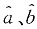
分别是a、b的最小二乘估计,选项C对;
由于
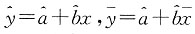
,两式相减:
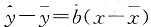
,所以选项D对.答案为A.
9. 设随机变量X
1,X
2,…,X
n…相互独立,它们满足大数定理,则X
i的分布可以是______
A.
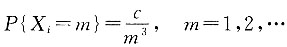
B.X
i服从参数为
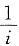
指数分布
C.X
i服从参数为i的泊松分布
D.X
i的密度函数
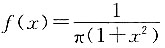
A B C D
A
[解析] 只要判断此序列是否独立同分布,且数学期望存在;或独立但分布不同,而数学期望、方差都存在,且方差一致有界即可.选项A中X
i独立同分布,且
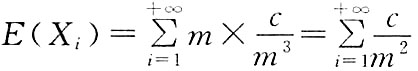
,级数
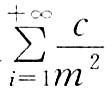
收敛,因此E(X
i)存在.选项D中X
i独立同分布,但E(X
i)不存在,因为
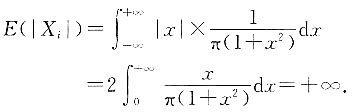
选项B、选项C中X
i不同分布,且选项B中D(X
i)=i
2,选项C中D(X
i)=i,均是i的无界函数.
二、填空题1. 随机变量X的概率密度
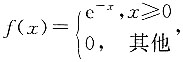
则E(2X)=______.
2
[解析]
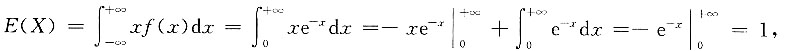
E(2X)=2E(X)=2.
2. 设随机变量X服从(-2,2)上的均匀分布,则随机变量Y=X
2的函数F
Y(y)=______.
[解析] 分析:已知X~f
X(x),x∈(-2,2)
当y<0时,F
Y(y)=P(Y≤y)=P(X
2≤y)=0,
当0≤y<2时,
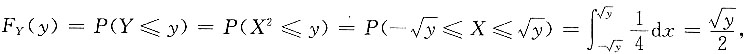
当y≥2时,
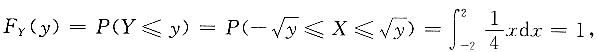
即
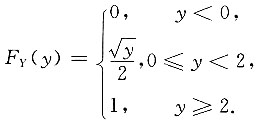
3. 设随机变量X和Y相互独立,且X~B(10,0.3),y~G(0.6),则Z=2X-3Y-5的数学期望为______,方差为______.
-4,18.4
[解析] 因X~B(10,0.3),Y~G(0.6),因此
E(X)=10×0.3=3,D(X)=10×0.3×0.7=2.1,
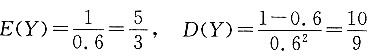
,故
E(Z)=E(2X-3Y-5)=2E(X)-3E(Y)-5
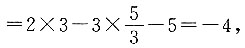
D(Z)=D(2X-3Y-5)=2
2D(X)+(-3)
2D(Y)

4. 设X
1,X
2,…,X
n为来自正态总体N(μ,σ
2)的简单随机样本,其中参数μ和σ
2未知,记
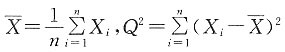
,则假设H
0:μ=0的t检验使用统计量t=______.
[解析] t检验,
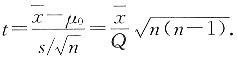
5. 已知连续型随机变量X的分布函数为F(x)=A+Barctanx,-∞<x<+∞系数A和B分别为______.
三、计算题设一批产品共2000个,其中有40个次品,随机抽取100个样品,求样品中次品数X的分布列,分别按下列方式抽样:1. 不放回抽样.
解:随机变量X的可能的值为0,1,2,…,40,由于是不放回抽样,所以由古典概型求概率的计算公式,X的分布列为:

2. 放回抽样.
解:随机变量X的可能的值为0,1,2,…,40,由于是放回抽样,所以可看成做了100次重复独立试验,随机变量X服从二项分布,则有X的分布列为:
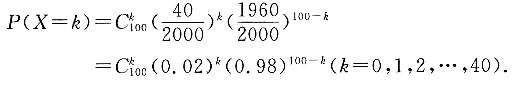
注意:不放回抽样和放回抽样不仅概率分布不同,而且随机变量X的可能的值也不同.
3. 若有n把看上去样子相同的钥匙,其中只有一把能打开门上的锁,用它们去试门上的锁,设取到每只钥匙是等可能的.若每把钥匙试开一次后除去,试求试开次数X的数学期望.
解:由题意知X的所有可能取值为:1,2,…n.且有
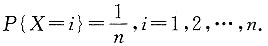
干暑X的分布律为:
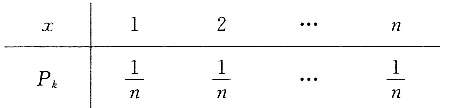
因此
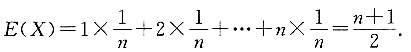
四、综合题1. 已知20世纪四个年度的一英里赛跑的世界纪录见下表:
| 年份x(年) | 43 | 45 | 58 | 67 |
| 纪录y(秒) | 242.6 | 241.4 | 234.5 | 231.1 |
为了用曲线
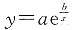
拟合这些数据,试计算a,b的估计
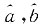
的值,并预测75年的世界纪录.
先把此非线性回归问题线性化,
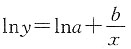
令y'=lny,a'=lna,
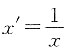
.则回归方程为y'=a'+bx',现列表计算如下:
| i
|
x'i
|
y'i
|
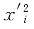
|
x'iy'i
|
| 1
|
0.023
|
5.49
|
0.000529
|
0.12627
|
| 2
|
0.022
|
5.486
|
0.000484
|
0.120692
|
| 3
|
0.017
|
5.46
|
0.000289
|
0.09282
|
| 4
|
0.015
|
5.443
|
0.000225
|
0.081645
|
| 计
|
0.077
|
21.879
|
0.001527
|
0.421427
|
据此可求出
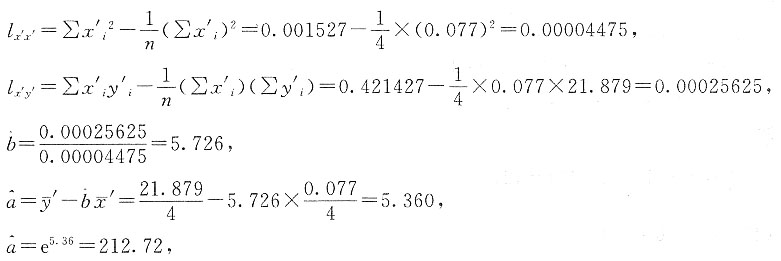
所以,回归直线为y'=5.360+5.726x'
相应的回归曲线方程为:
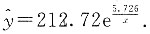
当x=75时,预测值为
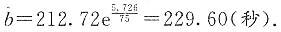
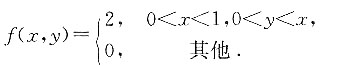
求:2. 关于X的边缘密度f
X(x).
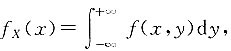
当0<x<1时,
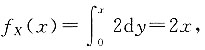
当x≤0或x>1时,f
X(x)=0
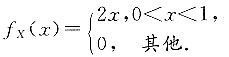
五、应用题1. 设总体X的均值为μ,方差为σ
2,其中σ
2为未知参数,又x
1,x
2,…,x
n为样本,且
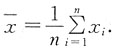
证明:
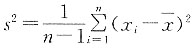
为σ
2的无偏估计.
2. 对两批同类电子元件的电阻进行测试,各抽6件,测得结果如下(单位:Ω):
A批:0.140,0.138,0.143,0.141,0.144,0.137;
B批:0.135,0.140,0.142,0.136,0.138,0.141.
已知元件服从正态分布,设α=0.05,问:
(1)两批元件的平均电阻是否有显著差异;
(2)两批元件的电阻的方差是否相等.
依题意提检验问题
(1)
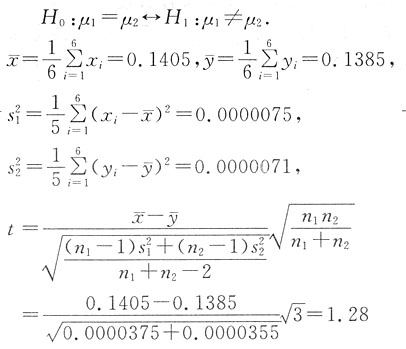
α=0.05,n
1=6,n
2=6,查表得
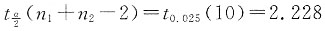
,
因为|t|<t
0.025(10),所以接受H
0,即认为两批元件的平均电阻无显著差异.
(2)
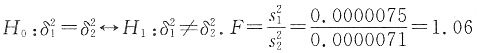
α=0.05,n
1=6,n
2=6,查表得
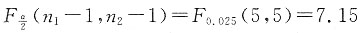
,因为F<F
0.025(5,5),所以接受H
0,即认为两总体的方差是相等的.
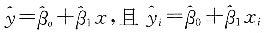 ,i=1,2,…,n,则估计参数β0,β1应使______
,i=1,2,…,n,则估计参数β0,β1应使______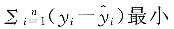
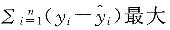
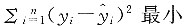
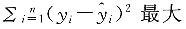
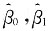 ,使
,使 ,其中右端min是对一切β0,β1的容许值取的Q的最小值.答案为C.
,其中右端min是对一切β0,β1的容许值取的Q的最小值.答案为C.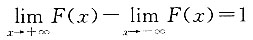
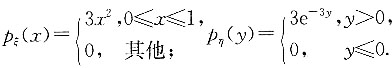 若ξ与η不相关,E(ξη)=
若ξ与η不相关,E(ξη)=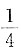
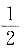
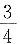
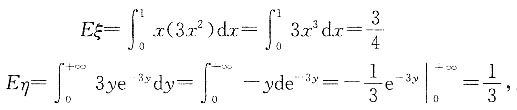 又ξ和η不相关,则
又ξ和η不相关,则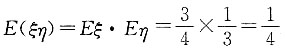 .
.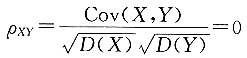 知X与Y不相关,故选B,其他选项由于条件不足,无法判定.
知X与Y不相关,故选B,其他选项由于条件不足,无法判定.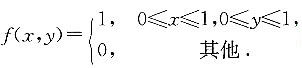 则X与Y______
则X与Y______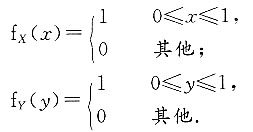
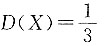
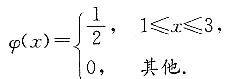
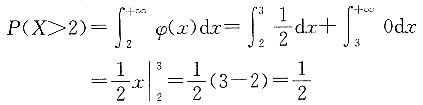 ,所以B对.
,所以B对.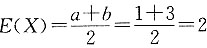 ,所以C对.
,所以C对.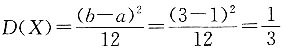 ,所以D对.
,所以D对.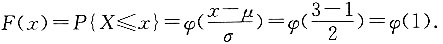
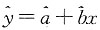 ,则______不成立(其中
,则______不成立(其中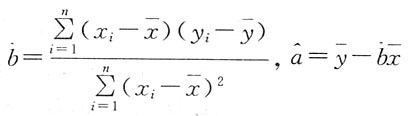 )
)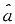 是a的有偏估计
是a的有偏估计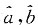 分别是a,b的极大似然估计
分别是a,b的极大似然估计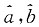 分别是a,b的最小二乘估计
分别是a,b的最小二乘估计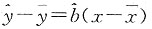
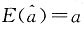 ,所以
,所以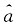 是a的无偏估计,选项A错;
是a的无偏估计,选项A错;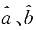 分别是a、b的极大似然估计,选项B对;
分别是a、b的极大似然估计,选项B对;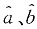 分别是a、b的最小二乘估计,选项C对;
分别是a、b的最小二乘估计,选项C对;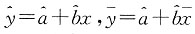 ,两式相减:
,两式相减: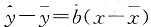 ,所以选项D对.答案为A.
,所以选项D对.答案为A.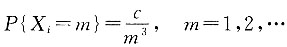
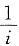 指数分布
指数分布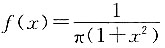
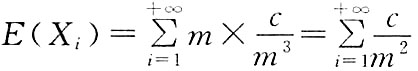 ,级数
,级数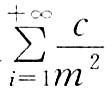 收敛,因此E(Xi)存在.选项D中Xi独立同分布,但E(Xi)不存在,因为
收敛,因此E(Xi)存在.选项D中Xi独立同分布,但E(Xi)不存在,因为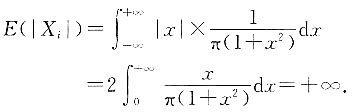
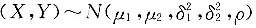 ,若ρXY=0,则______
,若ρXY=0,则______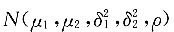 ,则ρXY=ρ=0,∴X与Y不相关,且X与Y相互独立.
,则ρXY=ρ=0,∴X与Y不相关,且X与Y相互独立.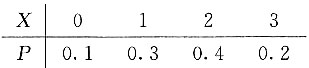 ,F(x)为其分布函数,则F(2)=______
,F(x)为其分布函数,则F(2)=______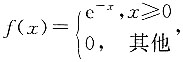 则E(2X)=______.
则E(2X)=______.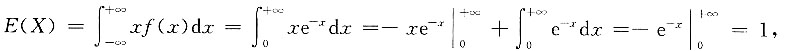 E(2X)=2E(X)=2.
E(2X)=2E(X)=2.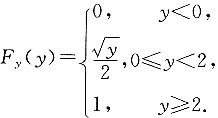
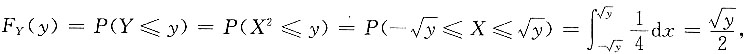
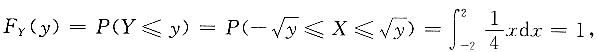
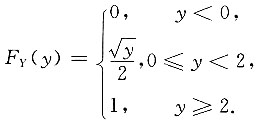
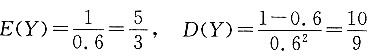 ,故
,故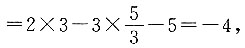

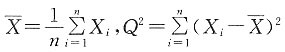 ,则假设H0:μ=0的t检验使用统计量t=______.
,则假设H0:μ=0的t检验使用统计量t=______.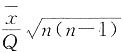
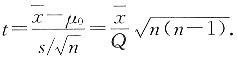
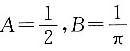
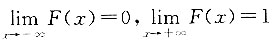 ,可得
,可得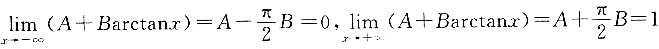
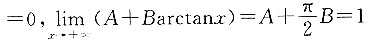 ,由此得
,由此得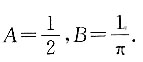

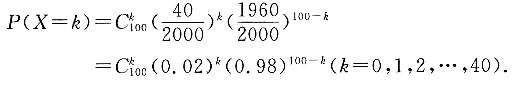
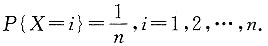
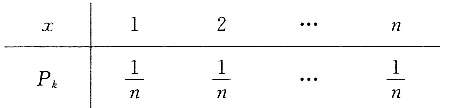
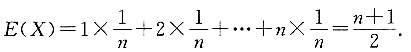
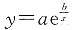 拟合这些数据,试计算a,b的估计
拟合这些数据,试计算a,b的估计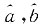 的值,并预测75年的世界纪录.
的值,并预测75年的世界纪录.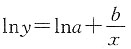
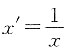 .则回归方程为y'=a'+bx',现列表计算如下:
.则回归方程为y'=a'+bx',现列表计算如下:
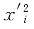
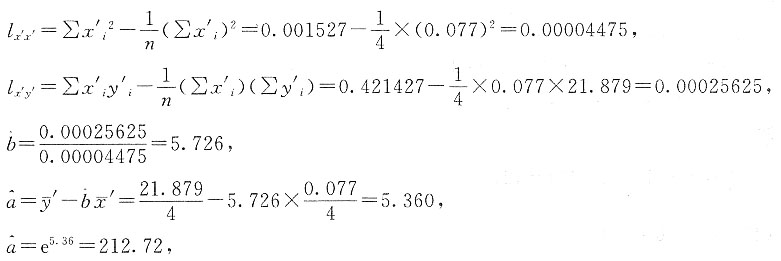
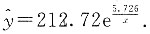
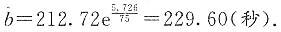
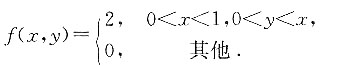
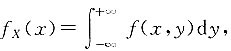
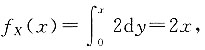
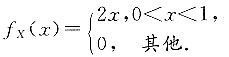
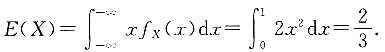
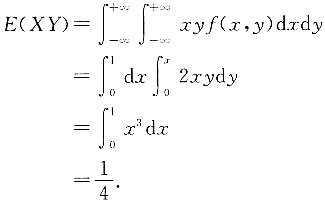
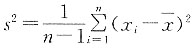 为σ2的无偏估计.
为σ2的无偏估计.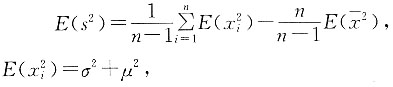
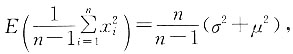

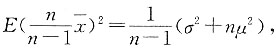
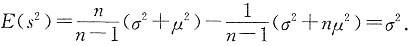
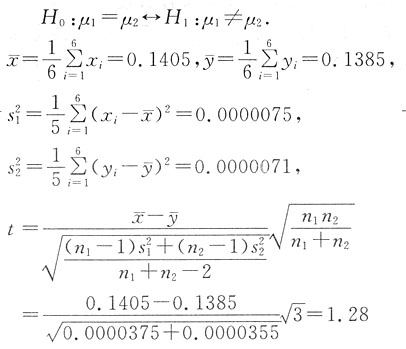
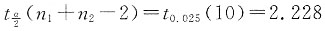 ,
,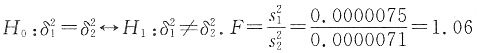
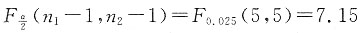 ,因为F<F0.025(5,5),所以接受H0,即认为两总体的方差是相等的.
,因为F<F0.025(5,5),所以接受H0,即认为两总体的方差是相等的.