一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的)1. 实二次型f(x
1,x
2,…,x
n)=X'AX为正定二次型的充要条件是______
- A.负惯性指数全为零
- B.对任意向量X=(x1,x2,…,xn)'≠0,都是X'AX>0
- C.|A|>0
- D.存在n阶矩阵P,使A=P'P
A B C D
B
[解析] 因为B恰是正定二次型的定义.A错.如
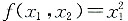
,这里
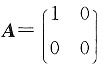
知道f(x
1,x
2)虽然负惯性指数为零,但不是正定二次型,因为取

时,f(x
1,x
2)=0.C错.如
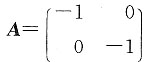
不管|A|=1>0,但因为它的一阶主子式-1<0,知f(x
1,x
2)=X'AX也不是正定二次型.D错.
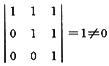
如
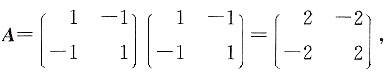
知|A|=0,故实二次型f(x
1,x
2)=X'AX不正定.答案为B.
4. 二次型
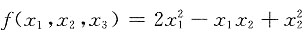
的矩阵为______
A.
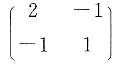
B.
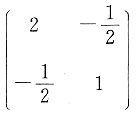
C.
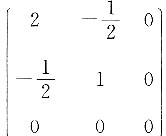
D.

A B C D
C
[解析] 因为有3个未知数,所以是三元实二次型,a
12+a
21=-1,又因为a
12=a
21,所以
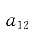
.答案为C.
二、填空题1. 向量α=(2,4),β=(a,-1)若α⊥β,则a=______.
2. 设3阶矩阵A的特征值为1,-2,3,则|A
2+E|=______.
3. 二次型f(x
1,x
2,x
3)=x
1x
2+x
2x
3的矩阵为______.
4. 已知方阵A相似于对角矩阵
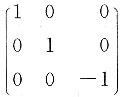
,则A
10=______.
5. 若三阶矩阵
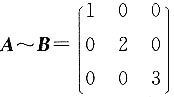
,则A的三个特征向量的关系为______.
线性无关
[解析] A~B知A和B有相同的特征值,故A有1,2,3三个不同的特征值,A为三阶的,故A的三个特征值对应的三个特征向量线性无关.
6. 设A为n阶矩阵,B为n阶非零矩阵,若B的每一个列向量都是齐次线性方程组Ax=0的解,则|A|=______.
0
[解析] 根据题意即Ax=0有非零解

|A|=0.
7. 向量组α
1=(1,1,0)
T,α
2=(3,0,-9)
T,α
3=(1,2,3)
T的秩为______.
8. 已知三阶方阵A的三个特征值为1,-2,-3,|A|及A
-1,A*,A
2+2A+E的特征值分别为______.
6;1,
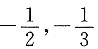
;6,-3,-2;4,1,4
[解析] 本题考查利用公式求特征值与特征向量,设λ
i为n阶方阵A的特征值,P
i为A的对应于特征值λ
i的特征向量,i=1,2,…,n,则
(1)f(A)的特征值为f(λ
i),对应于f(λ
i)的特征向量为p
i,i=1,2,…,n,其中f(x)为x的多项式;
(2)设A可逆,则A
-1的特征值为
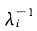
,对应的特征向量为p
i,i=1,2,…,n;
(3)设A可逆,则A*的特征值为
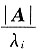
,对应的特征向量为p
i,i=1,2,…,n;
(4)A
T的特征值为λ
i,i=1,2,…,n,对应的特征向量为p
i,i=1,2,…,n;
(5)若B=P
-1AP,则B的特征值为λ,对应的特征向量为P
-1p
i,i=1,2,…,n;
从而有:|A|=1·(-2)·(-3)=6
A
-1的特征值为:
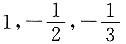
A*的特征值为:6,-3,-2;
A
2+2A+E的特征值为:4,1,4.
9. 方阵
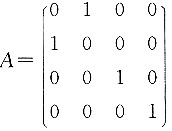
的全部特征值为______.
λ1=λ2=λ3=1,λ4=-1
[解析] A的特征多项式为
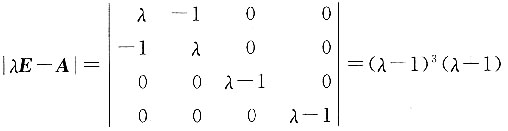
所以A的全部特征值为λ
1=λ
2=λ
3=1,λ
4=-1.
10. 设A,B均为2阶可逆矩阵,则
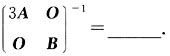
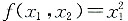 ,这里
,这里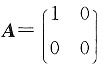 知道f(x1,x2)虽然负惯性指数为零,但不是正定二次型,因为取
知道f(x1,x2)虽然负惯性指数为零,但不是正定二次型,因为取 时,f(x1,x2)=0.C错.如
时,f(x1,x2)=0.C错.如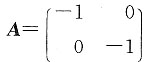 不管|A|=1>0,但因为它的一阶主子式-1<0,知f(x1,x2)=X'AX也不是正定二次型.D错.
不管|A|=1>0,但因为它的一阶主子式-1<0,知f(x1,x2)=X'AX也不是正定二次型.D错.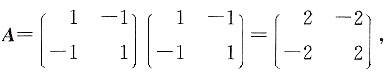
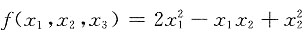 的矩阵为______
的矩阵为______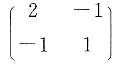
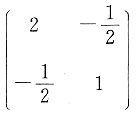
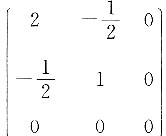

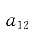 .答案为C.
.答案为C.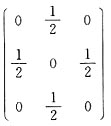
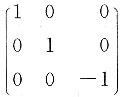 ,则A10=______.
,则A10=______.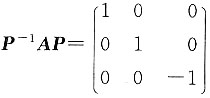 ,因此
,因此 所以
所以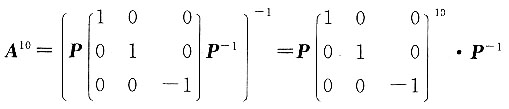
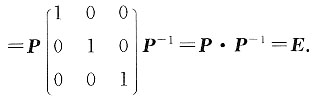
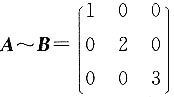 ,则A的三个特征向量的关系为______.
,则A的三个特征向量的关系为______. |A|=0.
|A|=0.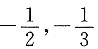 ;6,-3,-2;4,1,4
;6,-3,-2;4,1,4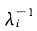 ,对应的特征向量为pi,i=1,2,…,n;
,对应的特征向量为pi,i=1,2,…,n;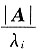 ,对应的特征向量为pi,i=1,2,…,n;
,对应的特征向量为pi,i=1,2,…,n;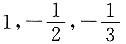
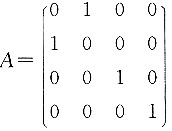 的全部特征值为______.
的全部特征值为______.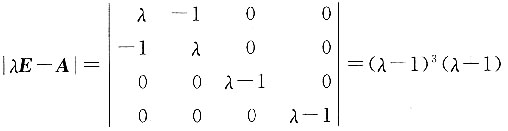
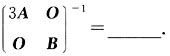

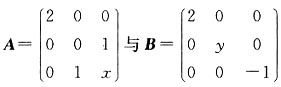 相似,求
相似,求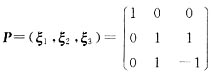 ,则P可逆,且P-1AP=B.
,则P可逆,且P-1AP=B.
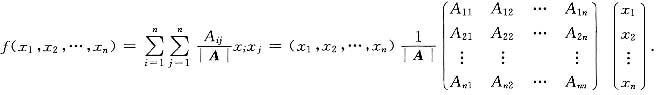
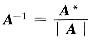 是实对称矩阵,于是A*是对称的,故二次型f(x)的矩阵是A-1.
是实对称矩阵,于是A*是对称的,故二次型f(x)的矩阵是A-1.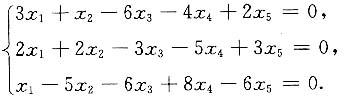
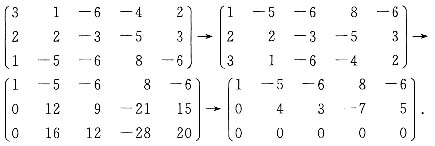
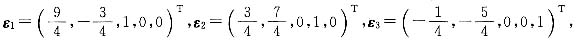
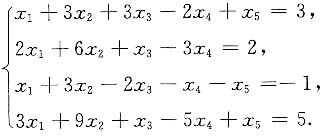

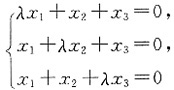 有非零解并求出其通解.
有非零解并求出其通解.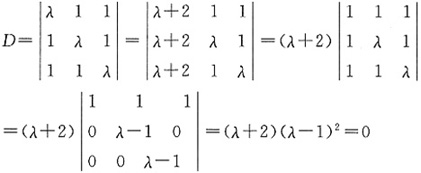
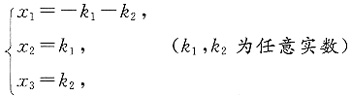

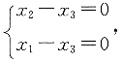 自由未知量为x3,方程组通解为
自由未知量为x3,方程组通解为
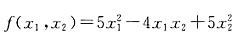 化为标准形.α1能否由α2,α3线性表示?证明你的结论.
化为标准形.α1能否由α2,α3线性表示?证明你的结论.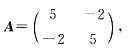
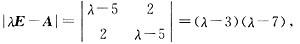
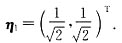
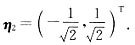
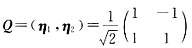 ,则Q为正交矩阵,
,则Q为正交矩阵,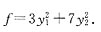
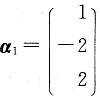 和
和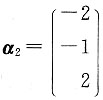 是A属于λ1=2和λ2=-1的特征向量,向量
是A属于λ1=2和λ2=-1的特征向量,向量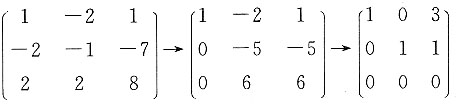
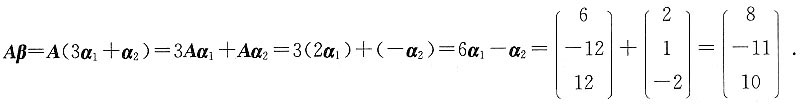
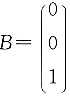 ,求矩阵方程AX=B的解.
,求矩阵方程AX=B的解.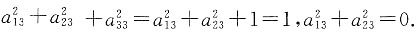 因此a13=a23=0;同理a31=a32=0即
因此a13=a23=0;同理a31=a32=0即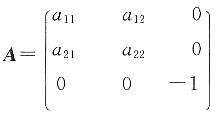 又A正交,因此A-1=AT,所以
又A正交,因此A-1=AT,所以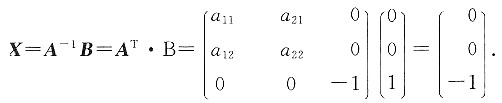
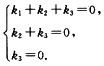
 ,
,