一、单项选择题(在每小题的四个备选答案中选出一个正确答案)
4. 下列函数中,当x→∞中,无穷小量是______
A.2
-x-1
B.
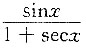
C.e
-x D.
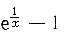
A B C D
D
[解析] 因为
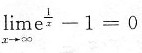
,所以当x→∞时,
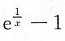
是无穷小.故应选D.
6. 设函数

则f(x)在x=1处______
- A.不连续
- B.连续但不可导
- C.连续且f'(1)=-1
- D.连续且f'(1)=1
A B C D
D
[解析] 因为
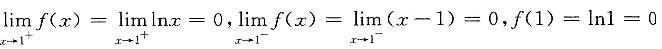
,
所以f(x)在x=1处连续.
又因为
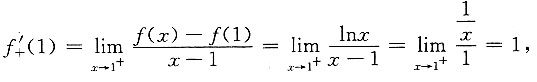

因为f(x)在x=1处可导且f'(1)=1,故应选D.
10. 在区间[-1,1]上下列函数中不满足罗尔定理的是______
A.f(x)=cosx
B.f(x)=3x
4+2
C.

D.f(x)=ln(1+x
2)
A B C D
C
[解析] 因为只有C项中

在[-1,1]上不连续,所以函数
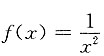
不满足罗尔定理,故应选C.
12. 设f'(2x-1)=e
x,则f(x)=______
A.
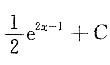
B.

C.

D.
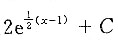
A B C D
B
[解析] 因为f'(2x-1)=e
x,所以
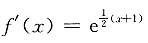
,
从而

故应选B.
15. 设f'(cos
2x)=sin
2x,且f(0)=0,则f(x)=______
A.

B.

C.

D.

A B C D
D
[解析] f'(cos
2x)=sin
2x=1-cos
2x,f'(x)=1-x,

,又f(0)=0得C=0,
所以
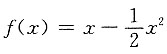
,故应选D.
16. 导数
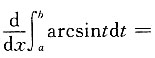
______
A.arcsinx
B.0
C.arcsinb-arcsina
D.
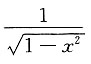
A B C D
B
[解析] 因为定积分

的值为常数,常数的导数等于0,所以
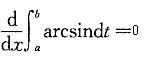
,故应选B.
17. 设区域D由直线x=a,x=b(b>a),曲线y=f(x),y=g(x)围成,则区域D的面积为______
A.
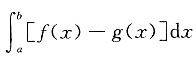
B.
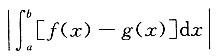
C.
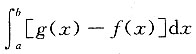
D.
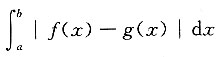
A B C D
D
[解析] 由定积分的几何意义可知,区域D的面积
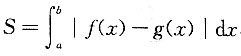
,故应选D.
18. 下列广义积分收敛的是______
A.
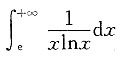
B.

C.

D.

A B C D
C
[解析]

,其他都是发散的,故应选C.
20. 设z=z(x,y)是由方程
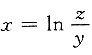
所确定的隐函数,则
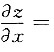
______
A B C D
D
[解析] 构造函数
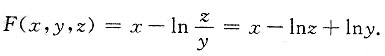
则
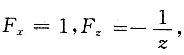
所以
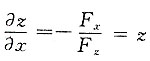
,而由

得z=ye
x,故应选D.
23. 交换二次积分

的积分次序后,I=______
A.

B.

C.

D.

A B C D
D
[解析] 因积分区域D为:D=D
1+D
2,其中
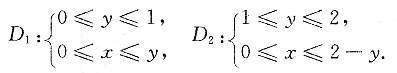
D又可表示为0≤x≤1,x≤y≤2-x,
于是交换次序后积分为

24. L是抛物线y
2=x上从点A(1,1)到B(1,-1)的一段弧,则∫
Lx
2dx+y
3dy=______
A.0
B.

C.
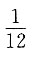
D.
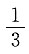
A B C D
A
[解析]
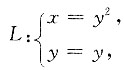
从1变到-1.
则

故应选A.
二、填空题1. 函数f(x)=1-ln(2x+1)的反函数为f(x)=______.
[解析] 由y=1-ln(2x+1)得ln(2x+1)=1-y,
即2x+1=e
1-y,所以
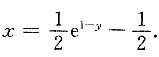
互换x、y得
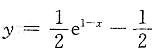
,x∈R.
故所求反函数为
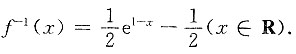
2.

______.
e6
[解析]
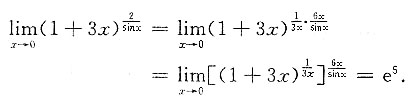
3. 该y=x
5+e
2x+3sinx,则y
(2015)=______.
22015e2x-3cosx
[解析] 因为(e
2x)
(n)=2
ne
2x,

,所以y
2015=2
2015e
2x-3cosx.
4. 点(0,1)是曲线y=x
3+ax
2+b的拐点,则a=______,b=______.
0,1
[解析] 由题设知f(0)=1,

所以b=1,a=0.
5. 设

,则f(x)=______.
[解析]

两边求导得
2f(2x-1)=e
-x-xe
-x(1-x)e
-x,
即
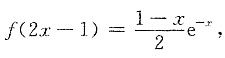
设t=2x-1则

,代入得
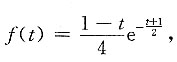
所以

6. 在空间直角坐标系中,以A(0,-4,1),B(-1,-3,1),C(2,-4,0)为顶点的△ABC的面积为______.
7. 若

______.
0
[解析] 因为z(x,0)=0,所以z
x(x,0)=0,故

8.

______.
π(e9-1)
[解析] D={(x,y)|x
2+y
2≤9}={(r,θ)|0≤θ≤2π,0≤r≤3},
所以

9. 若级数
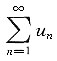
收敛于s,则级数

收敛于______.
2s-u1
[解析] 设s
n=u
1+u
2+…+u
n,
则(u
1+u
2)+(u
2+u
3)+…+(u
n+u
n+1)=2(u
1+u
2+…+u
n)+u
n+1-u
1 =2s
n+u
n+1-u
1,
又
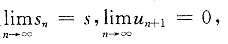
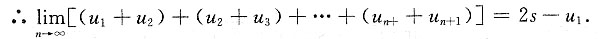
10. 以y=C
1+C
2x
2为通解的微分方程为______.
xy"-y'=0
[解析] y'=2C2x,y"=2C2,所以y'=xy",即xy"-y'=0.
三、计算题(每小题5分,共50分)
1. 求极限
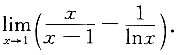
3. 求

4. 求定积分
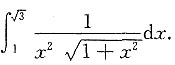
5. 已知x
2+z
2=yφ(z),其中φ为可微函数.求

F(x,y,z)=x
2+z
2-yφ(z),则F
x=2x,F
y=-φ(z),F
z=2z-yφ'(z),
所以

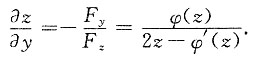
6. 计算

,其中D是由圆x
2+y
2=4与x=0所围的左半圆.
积分区域如图所示,在极坐标系下积分区域

所以

7. 求函数f(x,y)=e
2x(x+y
2+2y)的极值.
解方程组
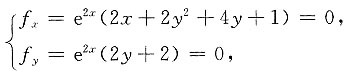
求得驻点为

f
xx=e
2x(4x+4y
2+8y+4),
f
xy=e
2x(4y+4),f
yy=2e
2x,
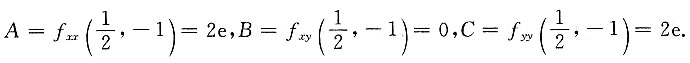
由于B
2-AC=-4e
2<0,且A>0
所以

为极小值点,函数的极小值为
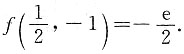
8. 求平行于x轴且经过两点(4,0,-2)和(5,1,7)的平面方程.
因为所求平面平行于x轴,故设所求平面方程为By+Cz+D=0.
将点(4,0,-2)及(5,1,7)分别代入方程得

因此所求平面的方程为

即9y-z-2=0.
9. 将函数
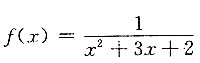
展开成(x+4)的幂级数.
10. 求微分方程2y"+y'-y=3e
x的通解.
对应齐次方程的特征方程为2r
2+r-1=0,
解得特征根为r
1=-1,
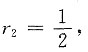
所以对应齐次方程的通解为
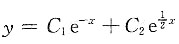
,(C
1,C
2为任意常数).
又因为λ=1不是特征根,可设特解为y
*=Ae
x,
代入原方程得2Ae
x+Ae
x-Ae
x=3e
x,解得
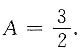
故所求方程的通解为
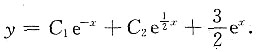
四、应用题(每小题7分,共14分)
1. 用汽船拖载重相同的小船若干只,在两港之间来回送货物,已知每次拖4只小船,一日能来回16次,每次拖7只,则一日能来回10次,若小船增多的只数与来回减少的次数成正比,问每日来回拖多少次,每次拖多少小船能使货运总量达到最大.
由已知,增加了3只船,减少6次,设每次拖x只船,则增加x-4只船,设减少y次,则3:6=(x-4):y,y=2(x-4),设运货总量为M.
则M=x[16-2(x-4)]=24x-2x2,x>0,
M'=24-4x=0,解得x=6,
又M"=-4<0,所以x=6为极大值点,
故一次拖6只船,每日来回12次能使货运量达到最大.
2. 设平面图形由曲线

和直线y=x,x=2及x轴围成.求:
(1)平面图形D的面积;
(2)这图形绕x轴旋转一周的体积.
平面图形如图所示.
取x为积分变量,且x∈[0,1]∪[1,2].
(1)平面图形D的面积为
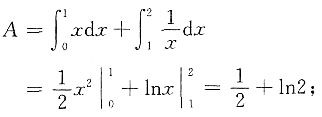
(2)平面图形绕x轴旋转一周所得旋转体的体积为

五、证明题1. 设f(x)在区间[0,1]上连续,且f(x)<1,证明:方程

在区间(0,1)内仅有一个实根.
【证明】 设

因为f(x)在[0,1]上连续,所以F(x)也在[0,1]上连续.
F(0)=-1<0,
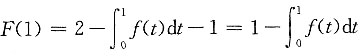
,由于f(t)<1,则
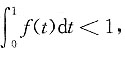
故F(1)>0,由零点定理可知至少存在一个ξ∈(0,1)使F(ξ)=0.
又因为F'(x)=2-f(x)>0,F(x)在(0,1)上单调增加,
因此方程
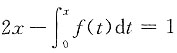
在(0,1)内仅有一个实根.
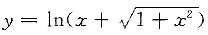 是______
是______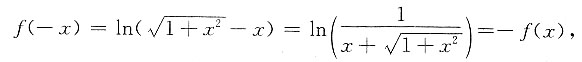
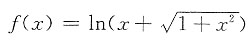 是奇函数,故选B.
是奇函数,故选B.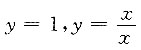
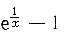
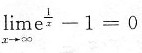 ,所以当x→∞时,
,所以当x→∞时,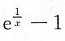 是无穷小.故应选D.
是无穷小.故应选D.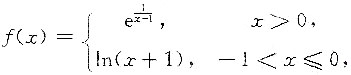 则x=0是f(x)______
则x=0是f(x)______ ,故选C.
,故选C. 则f(x)在x=1处______
则f(x)在x=1处______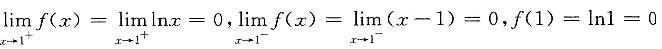 ,
,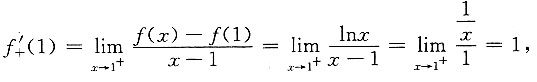

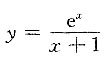
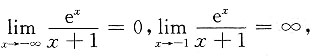

 在[-1,1]上不连续,所以函数
在[-1,1]上不连续,所以函数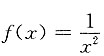 不满足罗尔定理,故应选C.
不满足罗尔定理,故应选C.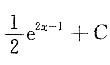


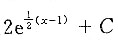
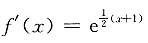 ,
, 故应选B.
故应选B.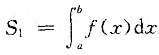 ,S2=f(b)(b-a),
,S2=f(b)(b-a),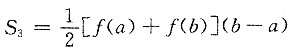 ,则 ______
,则 ______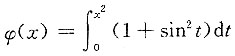 .则φ'(x)=______
.则φ'(x)=______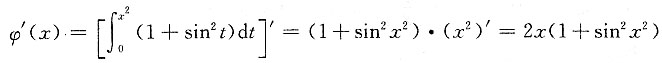 ,故应选D.
,故应选D.



 ,又f(0)=0得C=0,
,又f(0)=0得C=0,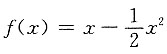 ,故应选D.
,故应选D.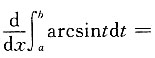 ______
______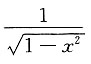
 的值为常数,常数的导数等于0,所以
的值为常数,常数的导数等于0,所以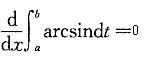 ,故应选B.
,故应选B.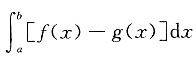
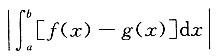
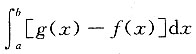
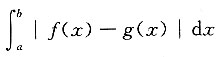
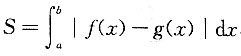 ,故应选D.
,故应选D.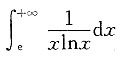



 ,其他都是发散的,故应选C.
,其他都是发散的,故应选C.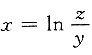 所确定的隐函数,则
所确定的隐函数,则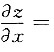 ______
______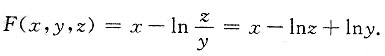
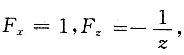
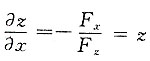 ,而由
,而由 得z=yex,故应选D.
得z=yex,故应选D.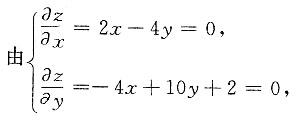 解得唯一驻点(-2,-1)故应选D.
解得唯一驻点(-2,-1)故应选D.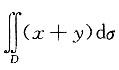 (其中D:|x|≤1,|y|≤1)=______
(其中D:|x|≤1,|y|≤1)=______ 的积分次序后,I=______
的积分次序后,I=______



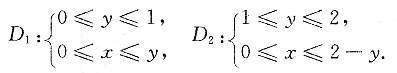


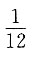
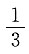
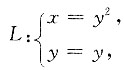 从1变到-1.
从1变到-1. 故应选A.
故应选A.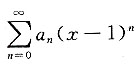 在x=-1处收敛,则此级数在x=2处______
在x=-1处收敛,则此级数在x=2处______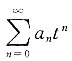 在t=-2处收敛,判断t=1处是否收敛的问题.根据阿贝尔定理可知,级数在t=1处绝对收敛.
在t=-2处收敛,判断t=1处是否收敛的问题.根据阿贝尔定理可知,级数在t=1处绝对收敛. 的和函数为______
的和函数为______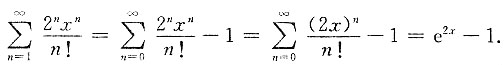 故应选B.
故应选B.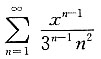 的收敛域为______
的收敛域为______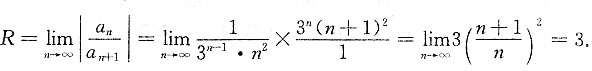
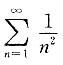 收敛,当x=-3时级
收敛,当x=-3时级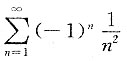 也是收敛的,因此收敛域为[-3,3],故应选C.
也是收敛的,因此收敛域为[-3,3],故应选C.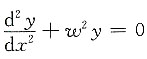 的通解是______
的通解是______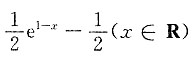
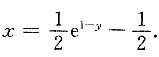 互换x、y得
互换x、y得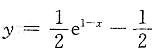 ,x∈R.
,x∈R.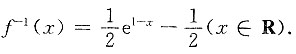
 ______.
______.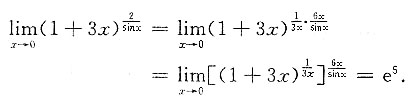
 ,所以y2015=22015e2x-3cosx.
,所以y2015=22015e2x-3cosx.
 ,则f(x)=______.
,则f(x)=______.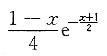
 两边求导得
两边求导得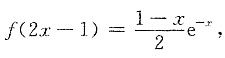
 ,代入得
,代入得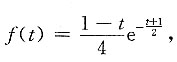

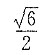
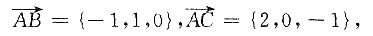
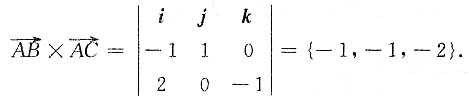
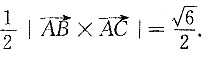
 ______.
______.
 ______.
______.
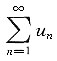 收敛于s,则级数
收敛于s,则级数 收敛于______.
收敛于______.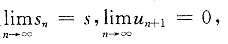
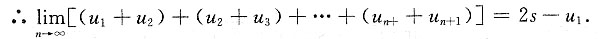
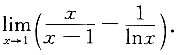
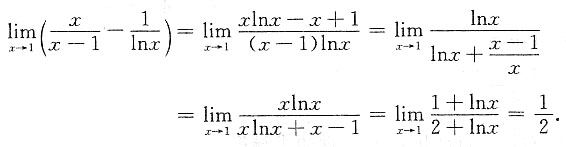
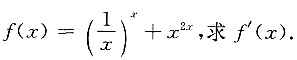
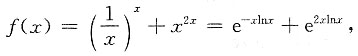
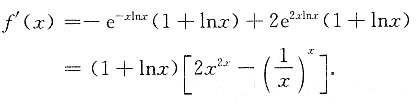


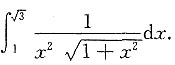



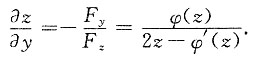
 ,其中D是由圆x2+y2=4与x=0所围的左半圆.
,其中D是由圆x2+y2=4与x=0所围的左半圆.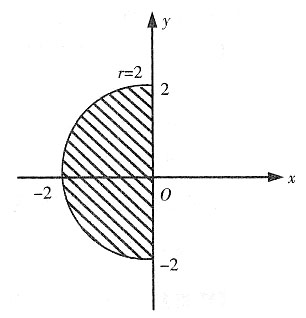


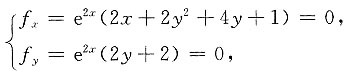

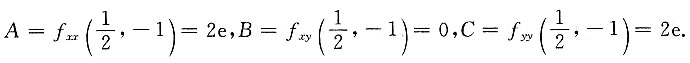
 为极小值点,函数的极小值为
为极小值点,函数的极小值为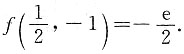


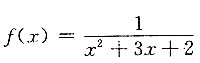 展开成(x+4)的幂级数.
展开成(x+4)的幂级数.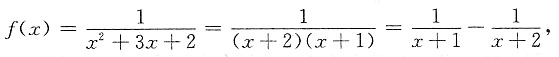
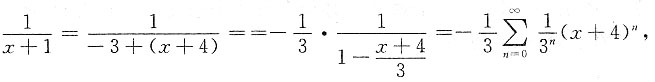
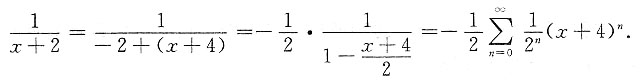

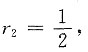
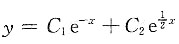 ,(C1,C2为任意常数).
,(C1,C2为任意常数).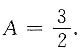
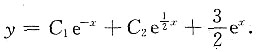
 和直线y=x,x=2及x轴围成.求:
和直线y=x,x=2及x轴围成.求:
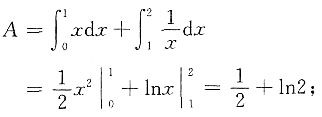

 在区间(0,1)内仅有一个实根.
在区间(0,1)内仅有一个实根.
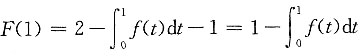 ,由于f(t)<1,则
,由于f(t)<1,则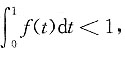
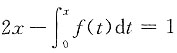 在(0,1)内仅有一个实根.
在(0,1)内仅有一个实根.