一、填空题1. 力法方程δ
21X
1+δ
22X
2+Δ
2P=0中,Δ
2P表示______,Δ
21X
1+δ
22X
2+Δ
2P表示______。
基本结构在外荷载单独作用下沿X2方向产生的位移;基本结构在X1、X2和外荷载共同作用下沿X2方向产生的位移。
2. 力法方程的物理意义是______。
基本结构中,在未知力和外界因素作用下,沿多余未知力方向产生的位移与原结构中相应的位移相等。
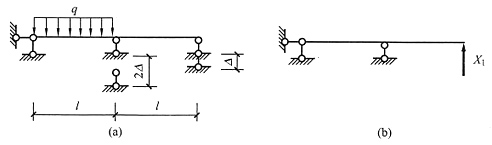
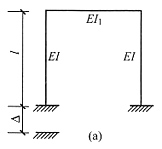
3. 图(a)所示结构中弹簧柔度f从小到大时,固定端弯矩M的变化规律是______。
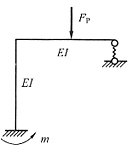
(a)
从小到大
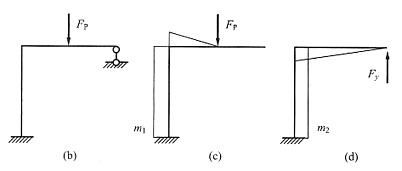
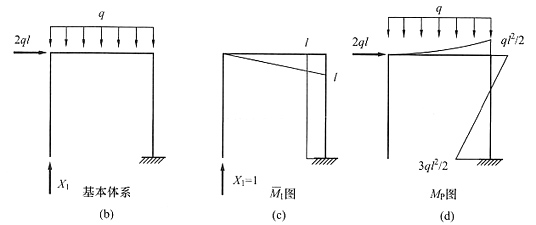
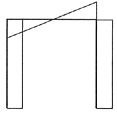
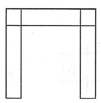
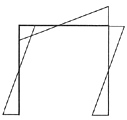
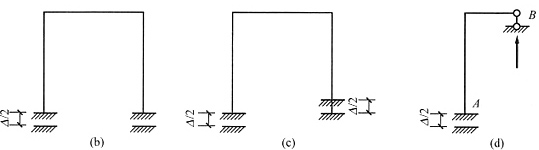
[解析] 做这类刚度按规律变化的题目通常可取两个极端情况,即先把弹簧刚度k按无穷大考虑,再按零考虑,比较两者的不同。当k→∞时,相当于刚性链杆支座[见下图(b)],弯矩图可以分成下图(c)和下图(d)叠加,两图中固定端的弯矩方向相反,两者应相减。当k→0时,就相当于没有弹簧支座,弯矩为下图(c)。经比较易知,弹簧刚度越大(柔度越小),弯矩越小。
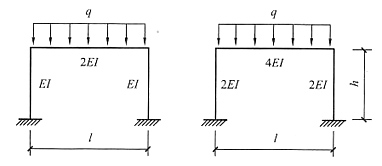
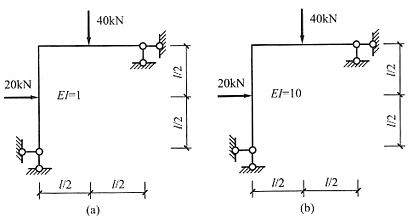
4. 下图(a)所示两结构中,若EI
2>EI
1,则横梁杆端弯矩M
BA及M
DC的大小关系为______。
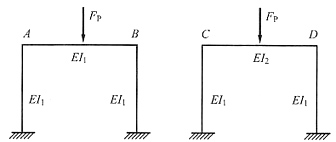
|MDC|<|MBD|
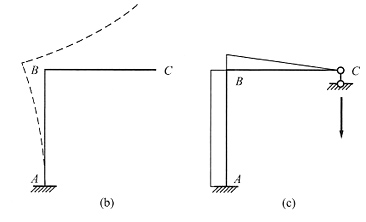
[解析] 与上两题类似,考虑EI
2→∞时的特殊情况,此时图(a)右图中两竖杆相对于水平杆刚度很小,相当于铰支座,见下图(b)。由图可得|M
DC|<|M
BA|。
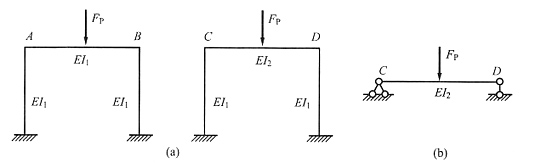
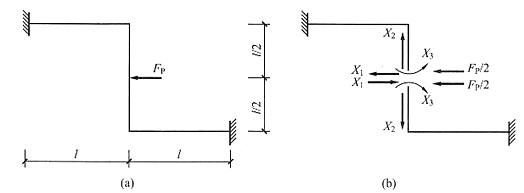
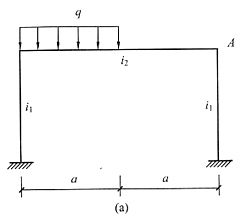
5. 计算下图(a)结构时,可简化为下图(b)计算的条件是______。
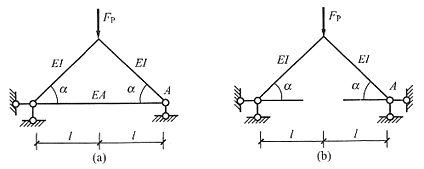
EA→∞
[解析] 当EA→∞时,A点无水平位移,符合固定铰支座的约束特点。
6. 对超静定结构,满足平衡条件的多余未知力有无穷多种解,既满足平衡条件又满足______条件的多余未知力有且仅有一种解。
7. 超静定结构内力与结构的刚度有关的理由是______。
确定超静定结构的内力不仅要考虑平衡方程,还要考虑变形协调条件。
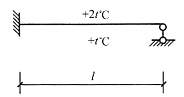
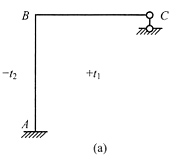
9. 原结构及温度变化(E
1I
1,α
1)下的M图如下图所示,若材料的有关特性改为(E
2I
2,α
2),且α
1/α
2=1.063,E
1I
1/E
2I
2=1.947,以外侧受拉为正,则MB=______。
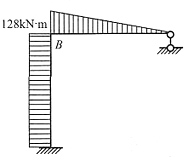
61.84kN·m
[解析] 本题的知识点是温度变化下的内力与EI及α的乘积成正比。根据已知条件得:
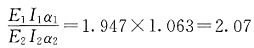
,因此M
B缩小为原来的2.07倍,即M
B2=128/2.07=61.84kN·m。
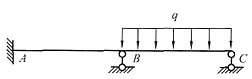
10. 下图所示结构中,AB杆的杆端弯矩M
BA=______。BC杆的轴力F
NBC=______。
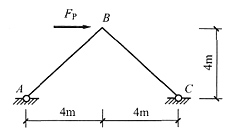
0;
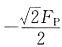
[解析] 当集中荷载作用在无线位移的结点上时,与该点相连的各杆无弯矩。经分析,B点无线位移,故杆AB、BC都无弯矩,只有轴力。根据B结点平衡方程可以求出BC杆的轴力。
11. 求解超静定结构时,必须综合考虑的三个方面条件是______、和______。
受力平衡条件;位移协调条件;物理条件(或本构方程)
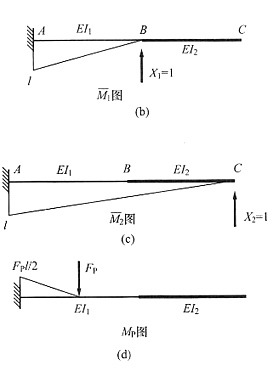
12. 图(a)所示结构,取B、C支座反力为力法基本未知量X
1、X
2。当EI
2增大时,力法方程中Δ
1P不变,Δ
2P______,δ
11______,δ
22______。(填“不变”、“变大”或“变小”)
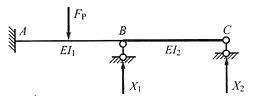
(a)
不变;不变;变小
[解析] 先画出
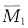
图、
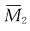
图和M
P图,见下图(b)、(c)(d);再用图乘法求系数,Δ
2P为
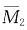
和M
P图乘,δ
11为
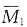
和
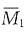
图乘,乘积中均不含EI
2,因此Δ
2P和δ
11这两个系数不变;而δ
22为
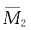
和
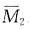
图乘,分母中含有EI
2,因此当EI
2增大时,δ
22减小。
13. 图(a)所示结构,EI=常数,在给定荷载作用下,支座A左、右截面的剪力F
QA左=______,F
QA右=______。
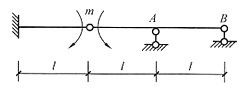
(a)
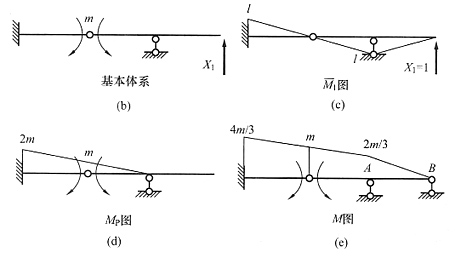
m/3l;2m/3l
[解析] 本题为一次超静定结构,需要先画出M图,再求剪力。取基本体系如图(b)所示,画出
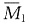
图和M
P图[见下图(c)、(d)],列出力法方程为δ
11X
1+Δ
1P=0;柔度系数
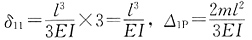
(算式略);将系数代入力法方程解得
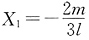
;由式
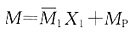
叠加得结构最后弯矩图,如下图(e)所示。由根据弯矩图求剪力的方法,可求得F
QA右=(m-2m/3)/l=m/3l(正号),F
QA右=(2m/3-0)/l=2m/3l(正号)。
14. 下图(a)所示体系,当采用下图(b)所示力法基本体系求解时,力法方程的右边项等于______。
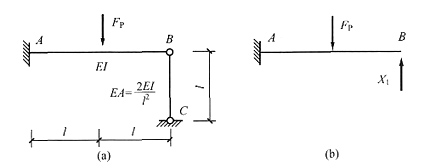
[解析] 本题属于桁架或组合结构中去除二力杆约束的解法。二力杆的受力如图(c)所示,力法方程右边项含义为原结构B点竖向位移,为
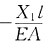
(可由BC杆B端位移求出,负号是指B端实际位移与X
1方向相反)。将

代入,则上式变为
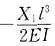
。
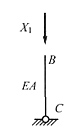
(c)
15. 图(a)所示组合结构中,BC链杆的轴力为______。
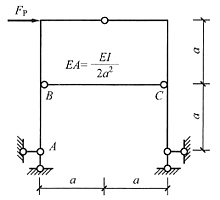
(a)
0
[解析] 本题一般荷载可以分解为正对称和反对称荷载。在正对称荷载下[见下图(b)]除DE杆受轴力外,其余杆无内力;在反对称荷载下,将BC杆从中间对称轴处截断,该杆轴力为正对称未知力,根据对称性的结论——反对称荷载下正对称的未知力为零,可知BC杆轴力为零。
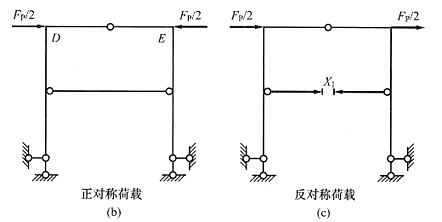
16. 图(a)所示结构(EI=常数)在所示荷载作用下,可直接判断出支座A的水平反力F
HA______。
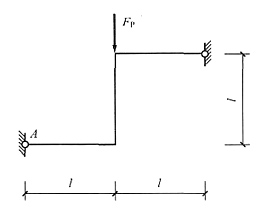
(a)
0
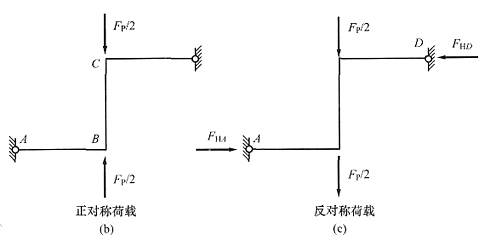
[解析] 本题也属于中心对称结构。将荷载分解为正对称和反对称荷载叠加,见下图(b)、(c)。正对称荷载下只有BC杆受轴压力,其余杆无内力;反对称荷载下,先由整体平衡条件得F
HA=F
HD,则F
HA和F
HD相当于正对称的未知力,根据结论——对称结构在反对称荷载下正对称的未知力为零,容易判断出F
HA=F
HD=0。
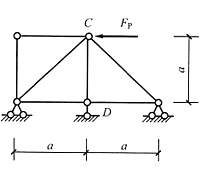
17. 下图所示超静定桁架在荷载作用下,杆件CD的轴力F
NCD=______。设备杆EA=常数。
0
[解析] 去掉左上角两根零杆,原结构变为对称结构受反对称荷载,根据桁架的对称性结论——在反对称荷载下对称轴处沿对称轴方向的杆为零杆,可得答案。
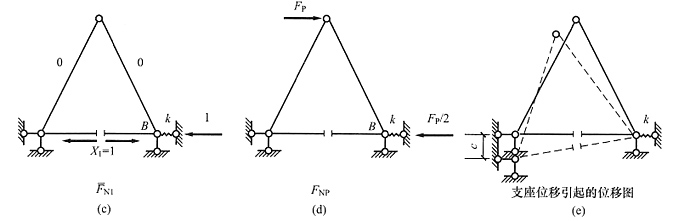
18. 图(a)所示桁架,各杆长度均为l,EA=常数;若采用图(b)所示的基本体系,则力法典型方程中的自由项Δ
1P=______。若该桁架无外荷载作用,但左支座发生了竖向位移c,同样采用图(b)所示的基本结构,则力法典型方程中的自由项Δ
1C=______。

FP/2k;0
[解析] (1)先求出

和F
NP示于图(c)、(d)中,
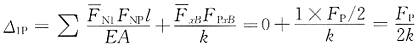
。
(2)支座位移引起的位移图见图(e),为刚体位移,从图中可以看出,沿X
1方向的相对位移为零,即Δ
1C=0。
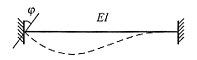
19. 图(a)所示结构,取图(b)所示基本结构,则力法方程为______,其中Δ
1C=______。
δ11X1+Δ1P+Δ1C=-Δ;-4Δ
[解析] 画出基本结构在支座位移下的位移图,见图(c),可以看出Δ
1C=-4Δ。
20. 图(a)所示结构力法的基本体系为图(b),力法典型方程为
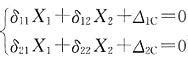
其中,自由项Δ
1C=______,Δ
2C=______。
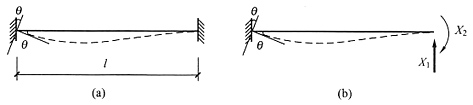
-θl;θ
[解析] 画出基本结构在转角θ作用下的位移图,见图(c),从图中可以看出Δ
1C=-θl,Δ
2C=θ。
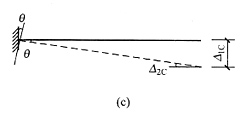
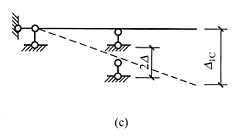
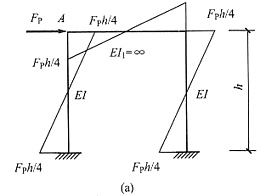
21. 已知图(a)所示结构M图,求A点水平位移______。
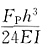
(向右)。
[解析] 取图(b)所示基本结构,并在A点加虚单位力。用图乘法,图(b)求面积,图(a)取竖标,则
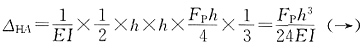
。
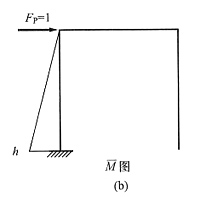
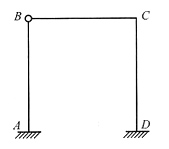
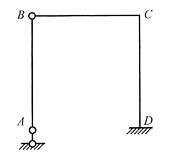
22. 图(b)为图(a)所示结构的力法基本体系,各杆EI=常数,k为弹簧刚度,则其力法方程的系数、自由项和右端项分别为:δ
11=______,Δ
1P=______,Δ=______。
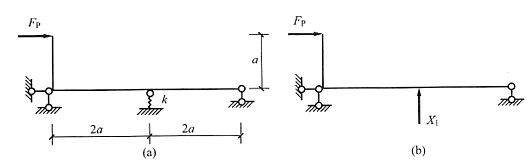
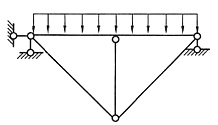
23. 下图所示结构中各杆EI=常数,在给定荷载作用下,H
A=______,V
A=______,M
CD=______。
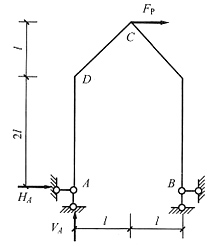
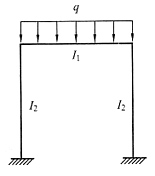
二、选择题7. 图(a)所示结构E=常数,在给定荷载作用下若使A支座反力为零,则应使______。

(a)
- A.I2=I3
- B.I2=4I3
- C.I2=2I3
- D.I3=4I2
A B C D
D
[解析] 用力法,把A支座看作多余约束,画出基本体系如下图(b)所示,
图和M
P图如下图(c)、(d)所示,力法方程δ
11X
1+Δ
1P=0。已知支座A反力等于零,即X
1=0,代入力法方程得Δ
1P=0,其中Δ
1P可以由
和M
P图乘得到,即

,整理得I
3=4I
2。
8. 下图(a)所示结构,取下图(b)为力法基本体系,EI=常数,则下述结果中错误的是______。
- A.δ23=0
- B.δ31=0
- C.Δ2P=0
- D.δ12=0
A B C D
D
[解析] 本题为中心对称结构,分别画出
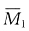
图、
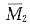
图、M
3图及M
P图,可知
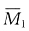
图、
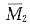
图是正对称的,
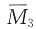
图、M
P图是反对称的,根据对称性的结论——正对称图形与反对称图形图乘结果为零,可知选项D错误。
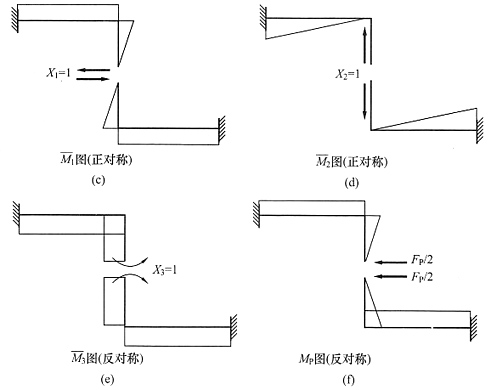
9. 图(a)所示结构支座A的弯矩M
A等于______。
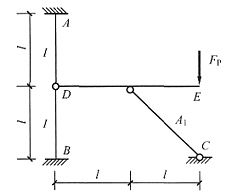
(a)
- A.FPl/2(右侧受拉)
- B.FPl/4(左侧受拉)
- C.FPl(右侧受拉)
- D.2FPl(右侧受拉)
A B C D
C
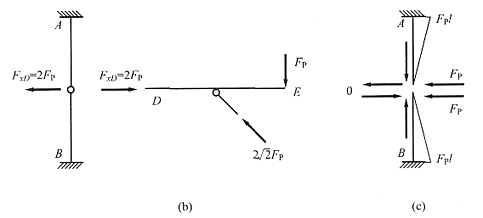
[解析] DEC为静定的附属部分,取DE杆作隔离体[见下图(b)],易求出F
xD=2F
P,将其作用于基本部分。此时基本部分为正对称结构受正对称荷载,从对称轴处去掉多余约束[见下图(c)],根据对称性结论可知反对称未知力为零,将集中荷载2F
P对称分配,可得每个固定端弯矩均为F
Pl,右侧受拉。
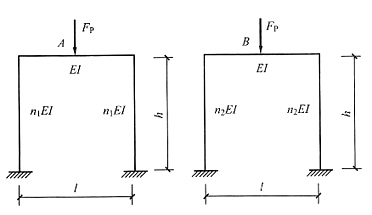
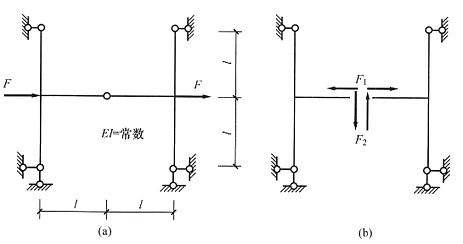
11. 图(a)、(b)所示两结构(EI=常数),右端支座均沉降Δ=1,两支座弯矩关系为______。
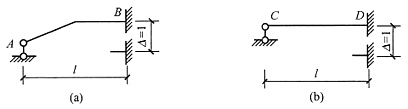
- A.MB>MD
- B.MB=MD
- C.MB<MD
- D.MB=-MD
A B C D
C
[解析] 画出(a)、(b)两图对应的

图及支座位移引起的位移图,分别见图(c)、(d)、(e)、(f),对应的力法方程分别为δ
11X
1+Δ
1C=0和
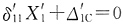
。两式系数的关系为
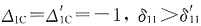
[因为图乘时图(c)中斜杆的长度大于图(e)中相应直杆的长度],因此
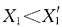
。而M
B=X
1l,
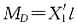
,所以M
B<M
D。

12. 图(a)所示对称无铰拱,全拱温度均匀升高t℃,则拱顶截面弯矩(以下侧受拉为正):______。
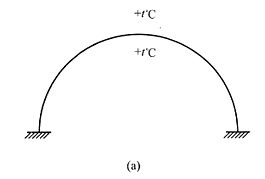
- A.为正值
- B.为负值
- C.为零
- D.正负不能确定,取决于截面变化规律
A B C D
B
[解析] (1)取半结构如图(b)所示,用力法解,画出基本体系[见图(c)]。
(2)列出第二个力法方程为δ
21X
1+δ
22X
2+Δ
2t=0。
(3)对各个柔度系数和自由项进行分析:δ
22为主系数,总大于零;δ
21为X
1=1引起的沿X
2方向的转角,从图(d)中的虚线所示位移图可以看出该转角与X
2方向相反,故为负值;
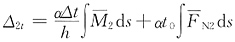
,其中Δt=0,t
0=t,
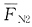
为X
2=1引起的轴力(为零),因此Δ
2t=0,这时力法方程变为Δ
21X
1+δ
22X
2=0。
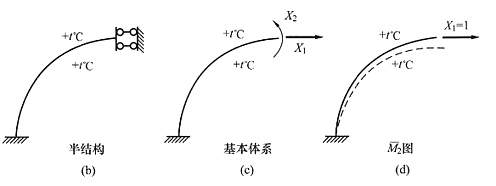
(4)由于经过上述分析得到的δ
21为负值,δ
22为正值,代入方程可得X
1和X
2符号相同。
(5)观察原结构,X
1为对称轴处的轴力,在温度升高时该力是挤压力,与假设方向相反,故X
1为负值,因此X
2必为负值,即上侧受拉。






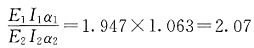 ,因此MB缩小为原来的2.07倍,即MB2=128/2.07=61.84kN·m。
,因此MB缩小为原来的2.07倍,即MB2=128/2.07=61.84kN·m。
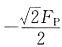

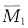 图、
图、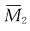 图和MP图,见下图(b)、(c)(d);再用图乘法求系数,Δ2P为
图和MP图,见下图(b)、(c)(d);再用图乘法求系数,Δ2P为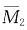 和MP图乘,δ11为
和MP图乘,δ11为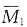 和
和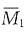 图乘,乘积中均不含EI2,因此Δ2P和δ11这两个系数不变;而δ22为
图乘,乘积中均不含EI2,因此Δ2P和δ11这两个系数不变;而δ22为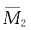 和
和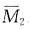 图乘,分母中含有EI2,因此当EI2增大时,δ22减小。
图乘,分母中含有EI2,因此当EI2增大时,δ22减小。

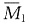 图和MP图[见下图(c)、(d)],列出力法方程为δ11X1+Δ1P=0;柔度系数
图和MP图[见下图(c)、(d)],列出力法方程为δ11X1+Δ1P=0;柔度系数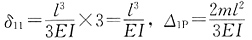 (算式略);将系数代入力法方程解得
(算式略);将系数代入力法方程解得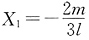 ;由式
;由式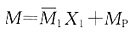 叠加得结构最后弯矩图,如下图(e)所示。由根据弯矩图求剪力的方法,可求得FQA右=(m-2m/3)/l=m/3l(正号),FQA右=(2m/3-0)/l=2m/3l(正号)。
叠加得结构最后弯矩图,如下图(e)所示。由根据弯矩图求剪力的方法,可求得FQA右=(m-2m/3)/l=m/3l(正号),FQA右=(2m/3-0)/l=2m/3l(正号)。

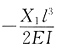
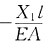 (可由BC杆B端位移求出,负号是指B端实际位移与X1方向相反)。将
(可由BC杆B端位移求出,负号是指B端实际位移与X1方向相反)。将 代入,则上式变为
代入,则上式变为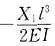 。
。






 和FNP示于图(c)、(d)中,
和FNP示于图(c)、(d)中,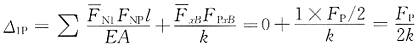 。
。


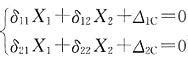 其中,自由项Δ1C=______,Δ2C=______。
其中,自由项Δ1C=______,Δ2C=______。


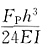 (向右)。
(向右)。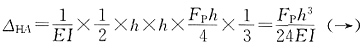 。
。



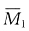 图、
图、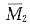 图和MP图都很容易画出,且自由项Δ1P=0,求其余系数时图乘也很方便;如果选其他基本体系,则弯矩图、图乘都会复杂一些,且没有等于零的副系数或自由项。
图和MP图都很容易画出,且自由项Δ1P=0,求其余系数时图乘也很方便;如果选其他基本体系,则弯矩图、图乘都会复杂一些,且没有等于零的副系数或自由项。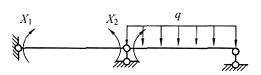

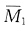 图和MP图如下图(c)、(d)所示,力法方程δ11X1+Δ1P=0。已知支座A反力等于零,即X1=0,代入力法方程得Δ1P=0,其中Δ1P可以由
图和MP图如下图(c)、(d)所示,力法方程δ11X1+Δ1P=0。已知支座A反力等于零,即X1=0,代入力法方程得Δ1P=0,其中Δ1P可以由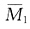 和MP图乘得到,即
和MP图乘得到,即 ,整理得I3=4I2。
,整理得I3=4I2。

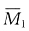 图、
图、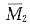 图、M3图及MP图,可知
图、M3图及MP图,可知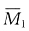 图、
图、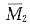 图是正对称的,
图是正对称的,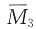 图、MP图是反对称的,根据对称性的结论——正对称图形与反对称图形图乘结果为零,可知选项D错误。
图、MP图是反对称的,根据对称性的结论——正对称图形与反对称图形图乘结果为零,可知选项D错误。


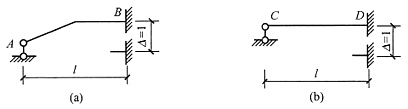
 图及支座位移引起的位移图,分别见图(c)、(d)、(e)、(f),对应的力法方程分别为δ11X1+Δ1C=0和
图及支座位移引起的位移图,分别见图(c)、(d)、(e)、(f),对应的力法方程分别为δ11X1+Δ1C=0和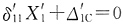 。两式系数的关系为
。两式系数的关系为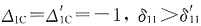 [因为图乘时图(c)中斜杆的长度大于图(e)中相应直杆的长度],因此
[因为图乘时图(c)中斜杆的长度大于图(e)中相应直杆的长度],因此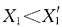 。而MB=X1l,
。而MB=X1l,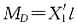 ,所以MB<MD。
,所以MB<MD。

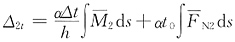 ,其中Δt=0,t0=t,
,其中Δt=0,t0=t,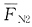 为X2=1引起的轴力(为零),因此Δ2t=0,这时力法方程变为Δ21X1+δ22X2=0。
为X2=1引起的轴力(为零),因此Δ2t=0,这时力法方程变为Δ21X1+δ22X2=0。

 图[见图(c)]与M图同侧受拉,因此可以断定图乘结果为正值,即A点水平位移向右。
图[见图(c)]与M图同侧受拉,因此可以断定图乘结果为正值,即A点水平位移向右。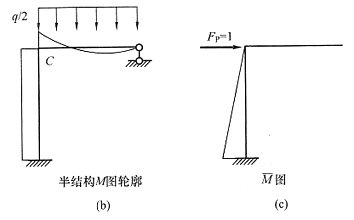
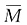 图见图(e),图中右支座的转角不出现,因为相应的约束已被去除,而左支座的转角应保留,该转角引起的位移图见虚线。图乘时
图见图(e),图中右支座的转角不出现,因为相应的约束已被去除,而左支座的转角应保留,该转角引起的位移图见虚线。图乘时 图求面积,M图取竖标,则
图求面积,M图取竖标,则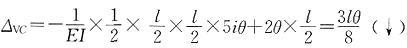 。
。