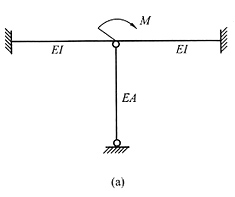
计算分析题1. 求解图(a)所示对称结构,并画出M图。
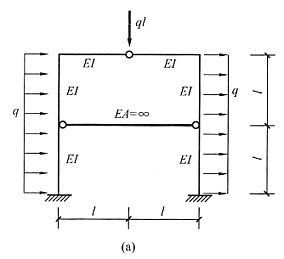
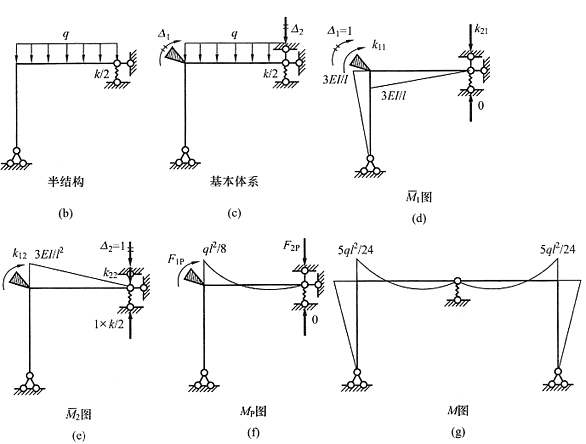
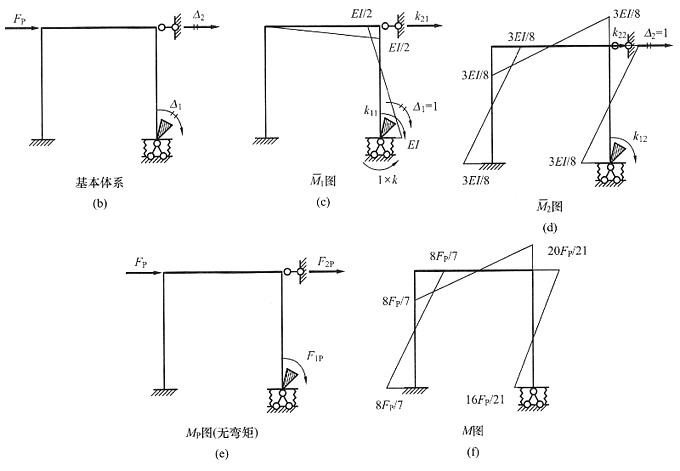
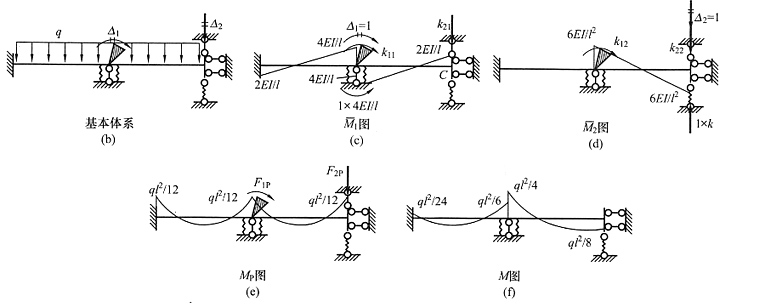
解 本题的荷载有正对称和反对称两种,用半结构求解。在正对称荷载下半结构见图(b)(中间的轴力杆没有位移,化为一链杆支座),反对称荷载下半结构见图(c)(根据反对称荷载下正对称的未知力为零判断出中间轴力杆轴力为零)。由于题目没有指定方法,因此可以选择最方便的方法。正对称半结构只有一个转角未知量,可用位移法或力矩分配法求解,过程略,正对称弯矩图见图(d);反对称半结构用力法最方便,过程略,反对称弯矩图见图(e)。叠加后的总弯矩图见图(f)。
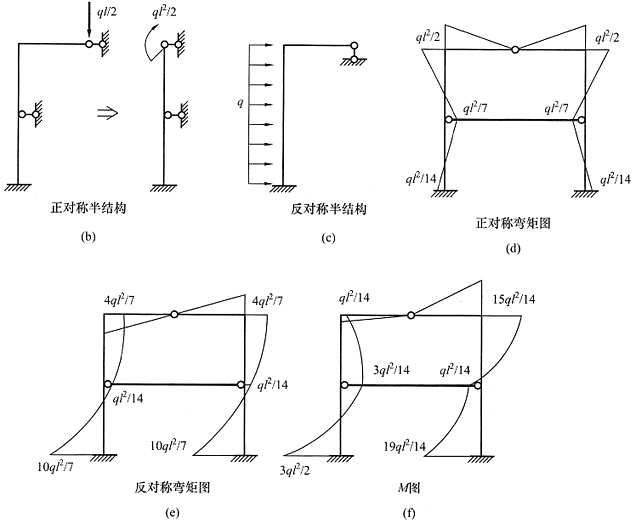
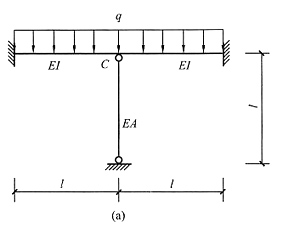
2. 所有杆件均不计轴向变形,用位移法计算图(a)所示结构并作M图,各杆EI=常数。
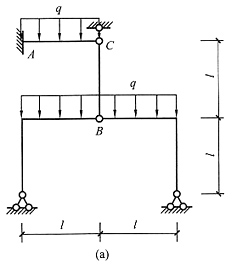
解 本例虽然从整体看不是对称结构,但上下层之间通过一根无轴向变形的轴力杆相连,结点B相当于下层的固定铰支座,仅看下层是对称的,可以简化为图(b)所示的半结构,有一个转角未知量,用位移法求解很方便,过程略。AC杆为一端固定一端铰支的单跨梁,可以直接画出弯矩图。综合后的结构总弯矩图见图(c)。
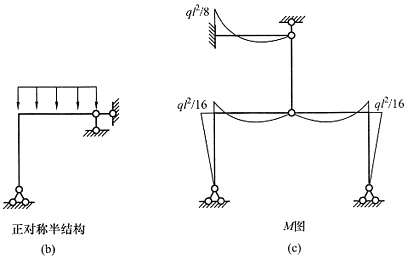
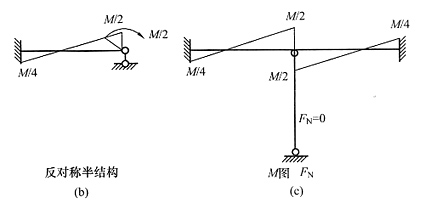
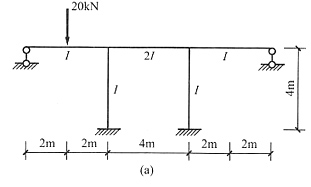
3. 画图(a)所示结构弯矩图和轴力图(可不写过程)。
解 本题为反对称荷载,根据本书第二章所讲对称性的零杆判断方法,可以判断出中间二力杆在反对称荷载下为零杆,简化半结构[见图(b)],不需计算即可画出弯矩图。水平杆由于不考虑轴向变形,轴力无法求出。综合以上分析,画出原结构弯矩图和轴力,见图(c)。
4. 已知图(a)所示结构C点的线位移为2ql
3/49i,EA =EI/2l
2,作M图。
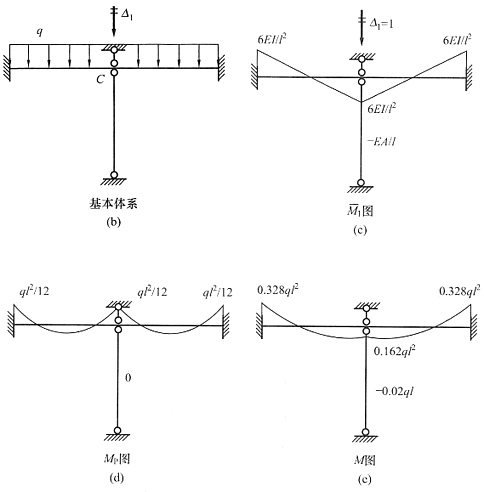
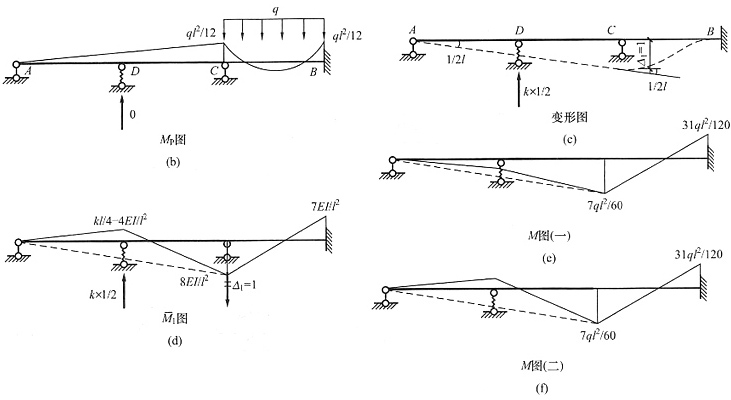
解 本题为正对称荷载,因此C结点无转角,只有一个线位移未知量,增加一个附加约束,基本体系见图(b),C点实际位移向下。
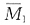
图和M
P图见图(c)、(d)。利用公式
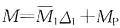
,并将C点线位移代入Δ
1叠加后得结构的弯矩图,见图(e)。
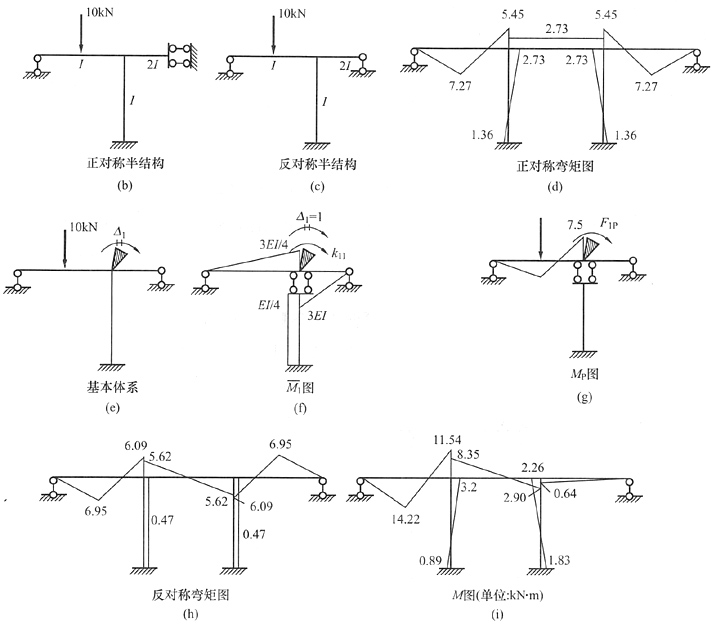
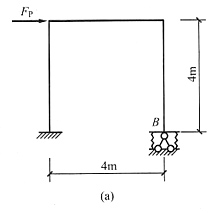
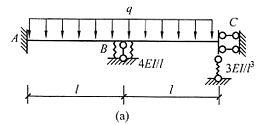
5. 利用对称性,并以最简便位移法计算图(a)所示结构,绘弯矩图,EI为常数。
解 将荷载分解成正对称和反对称荷载,并取相应的半结构[见图(b)、(c)]。正对称半结构只有一个结点转角未知量,计算过程略,正对称弯矩图见图(d)。
以下将重点讲解反对称荷载的计算。从图(c)可以看出,中间竖杆为剪力静定杆,可以不取水平位移未知量,只取转角未知量,这样做位移法未知量最少。基本体系见图(e)。继续画出
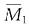
图和M
P图[见图(f)、(g)],注意中间竖杆上端水平位移是不受约束的,相当于定向结点(道理同渐进法中的无剪力分配法)。位移法方程k
11Δ
1+F
1P=0,k
11=4EI,F
1P=7.5,代入方程求解得Δ
1=-15/8EI,反对称荷载下的弯矩图见图(h)。将正反对称荷载的弯矩图叠加后得原结构弯矩图,见图(i)。
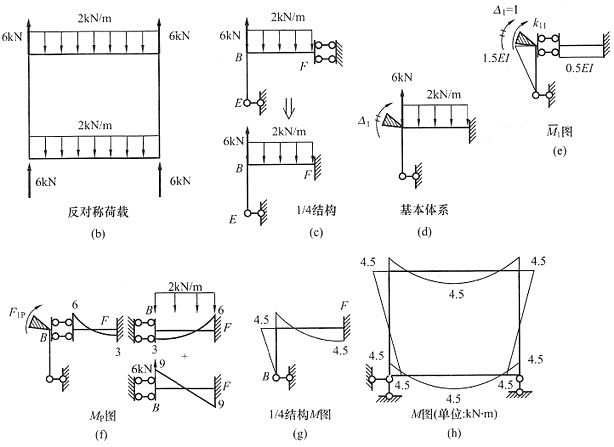
6. 考虑对称性,用位移法作图(a)所示结构的弯矩图,分布荷载方向向下。
解 先求出支座反力,并将其分解成正反对称荷载,在正对称荷载下无弯矩(前面已有不少这样的例题),反对称荷载见图(b)。从图(b)中可以看出,此时的荷载沿y轴是正对称,沿x轴是反对称,简化成1/4结构见图(c)。图(c)中的上图是直接从图(b)中简化来的,但是在竖向缺少约束,是几何可变体系,为保证其几何不变性,需要增加一个竖向约束(该约束的反力应等于零),在E点或F点加都可以,实际的1/4结构是(c)中的下图。求解时可以取两个未知量,也可以只取一个转角未知量(因为BF为剪力静定杆),本例选择后一种方法。增加一个附加约束,基本体系见图(d)。应注意画
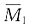
和M
P图时BF杆的B端相当于定向结点,M
P图中的BF杆弯矩图为两种荷载叠加。位移法方程为k
11Δ
1+F
1P=0,系数k
11=2EI,F
1P=-6kN·m,解方程得Δ
1=3/EI。1/4结构弯矩图见图(g),整个结构弯矩图见图(h)。
7. 试用位移法分析图(a)所示刚架并绘M图。设备杆的EI值相同。
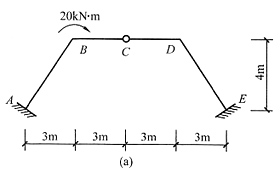
解 将荷载分解为正反对称并简化半结构,正对称半结构见图(b),不需计算可以直接画出弯矩图。反对称半结构见图(c),属于复杂的斜刚架,在此不再赘述,反对称半结构的弯矩图见图(d)。叠加后原结构的弯矩图见图(e)。
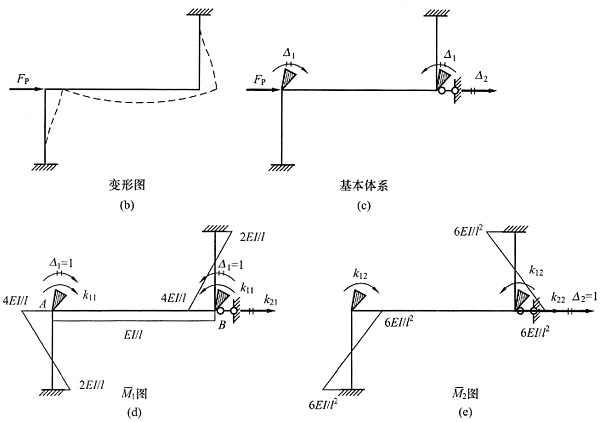
8. 用位移法作图(a)所示结构的弯矩图。各杆EI相同且为常数。
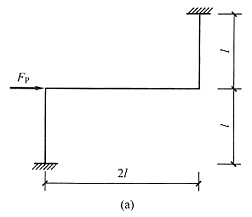
解 先大致画出变形图见图(b),从图中可以看出,整个结构为中心对称结构,有两个转角和一个水平位移,由于荷载反对称,因此两个转角的绝对值是相等的,方向也从图中容易看出,所以本题采用两个未知量计算,基本体系见图(c)。再画出
和M
P图,
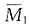
图中AB杆弯矩为两端固定杆在两端同时发生支座转角时产生的弯矩。位移法方程为
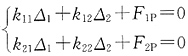
,求刚度系数和自由项应注意,k
11、k
12、F
1P应等于两个附加刚臂上的力之和,k
11=10EI/l,k
12=k
21=-6EI/l
2×2=-12EI/l
2,k
22=24EI/l
3,F
1P=0,F
2P=-F
P。将各系数代入位移法方程并求解,得Δ
1=F
Pl
2/8EI,Δ
2=5F
Pl
3/48EI。叠加得最后弯矩图见图(g)。
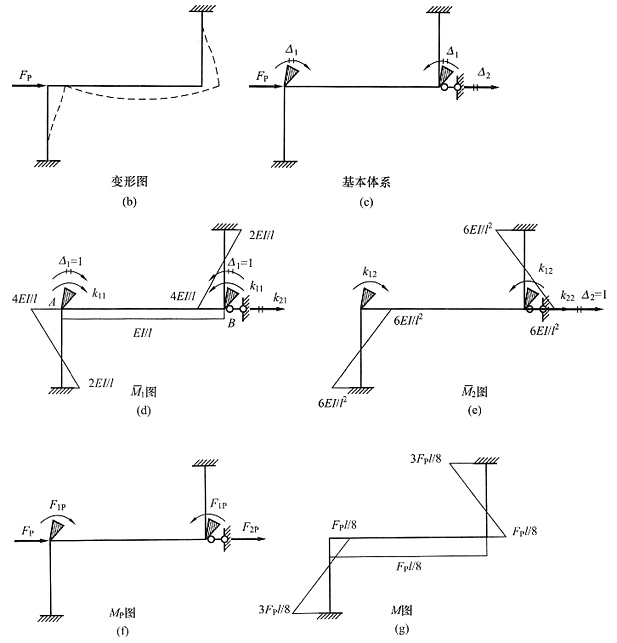
[解析] 本题是中心对称结构,其实用力法最简便,将荷载分解为正对称和反对称,正对称荷载下无弯矩,反对称荷载下对称轴处只有弯矩不为零,即只有一组未知量。但题目要求用位移法,具体求解过程如下。
9. 用位移法作图(a)所示结构M图。设备杆EI=常数。
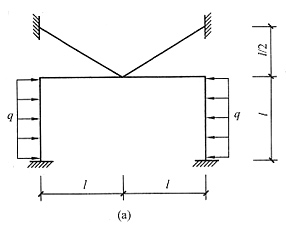
解 本题荷载正对称,且由于斜杆的作用,对称轴处的结点无位移,相当于固定支座,半结构见图(b),一个转角未知量,计算过程略。弯矩图见图(c)。
10. 利用对称性作出图(a)所示结构简化分析的计算简图,并进行计算(自选计算方法),作出原结构的弯矩图。
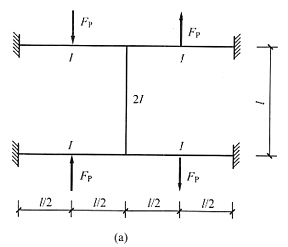
解 本题荷载沿y轴反对称,取半结构见图(b),该半结构又沿x轴正对称,简化为1/4结构见图(c)。用力矩分配法或位移法计算都很方便,过程略。1/4结构弯矩图见图(d),最后画出原结构弯矩图见图(e)。
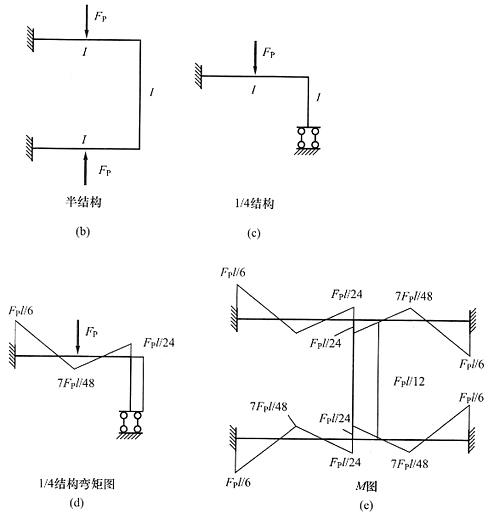
11. 用位移法计算图(a)所示结构,并作出M图。EI=常数。
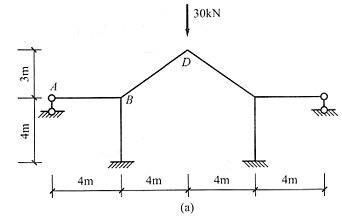
解 利用对称性取半结构,有两个未知量,B点转角和A点水平位移,位移法方程为
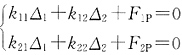
,
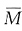
图、
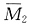
和M
P图见图(d)、(f)、(b)。画
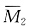
图时,应先弄清楚Δ
2=1时结构的变形图[见图(e)],B点左移单位位移至B'点,D点将下移至D'点,且应保证位移后的BD杆沿原方向的投影长度与原长相等,即BB' cosα=DD'sinα,将BB'=1代入求出DD'=4/3,接下来可以继续求出垂直于BD杆的位移分量,该位移分量作为BD两点的相对线位移,将引起BD杆的弯矩。求刚度系数和自由项的过程如下:
(1)由M
P图中B结点力矩平衡易得F
1P=0。求自由项F
2P时,根据M
P图,取隔离体[见图(c)]。由上图∑M
B=0得F
RA=0,再由下图∑M
0=0得,F
2P=-20kN。
(2)由
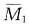
图中B结点力矩平衡可得
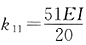
。
(3)再分析
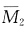
图。由结点B的力矩平衡得是
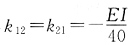
。求k
22时,见图(g)。在上图中,由∑M
B=0得F
RA=0,再由下图,∑M
O=0得,k
22=109EI/240。
将系数带入方程解得Δ
1=0.432/ET,Δ
2=44.06/EI,画出弯矩图,如图(h)所示。
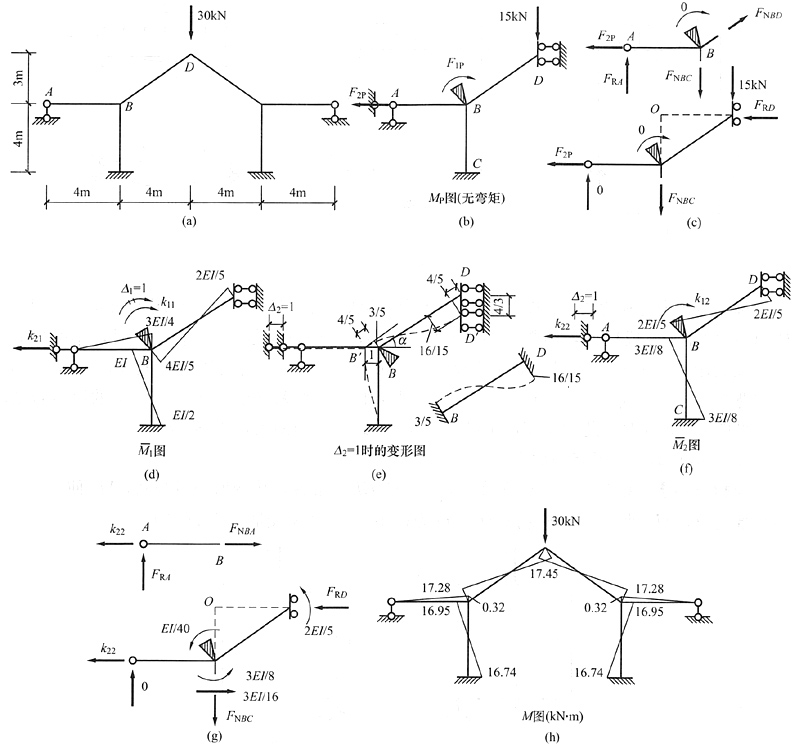
本题特点:本题中的斜杆两端位移方向不同,这时为保证杆长不变,两端位移是有比例关系的,需要准确找到这个比例关系才能画出弯矩图。这类题目是位移法中最复杂的一类。
12. 图(a)所示刚架中,梁的抗弯刚度、线刚度i
b=EI
b/l,柱的抗弯刚度EI
c、线刚度i
c=EI
c/h,梁柱线刚度比α=i
b/i
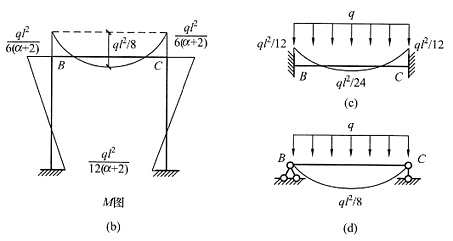
c。要求分析该刚架结构弯矩分布随梁柱线刚度比α的变化而变化的情况(提示:尤其要分析α→0及α→∞这两种特殊情况)。

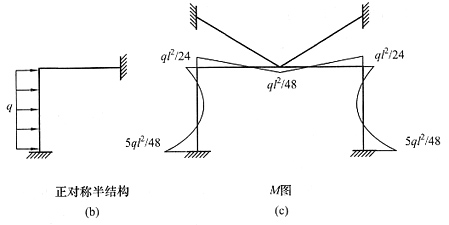
解 本题为对称荷载,可以简化半结构用位移法计算,过程略,弯矩图见图(b)。B、C点弯矩与α成反比,α越大,结点弯矩越小,跨中弯矩越大。当α→0时,梁刚度相对于柱无限小,柱相当于梁的固定支座,见图(c),此时支座弯矩最大,为ql
2/12,跨中弯矩最小,为ql
2/24。当α→∞时,柱刚度相对于梁无限小,柱相当于梁的固定铰支座,见图(d),此时支座弯矩最小,为0,跨中弯矩最大,为ql
2/8。
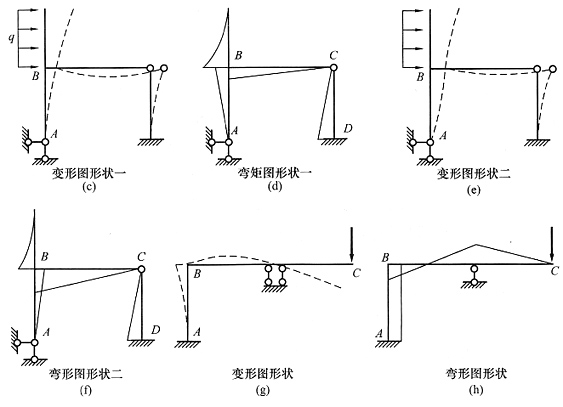
13. 画出图(a)、(b)所示结构弯矩图的轮廓,杆件抗弯刚度EI=常数。
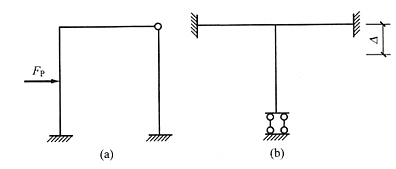
解 本题中的两图为超静定结构,应先画变形图的轮廓才能画出弯矩图轮廓。
(1)图(a)。先画出变形图[见图(c)]。变形的顺序是AB杆在荷载作用下先发生变形,B点和C点右移且B点顺时针转动,再由位移协调条件判断出BC杆向下弯曲,CD杆向右弯曲。注意,有些读者画出的变形图为图(d),两者的区别在于图(c)中BA杆有拐点,图(d)中无拐点,通过B结点的弯矩平衡可以判断,图(d)错误。再进一步根据变形图的弯曲侧画出弯矩图的形状,见图(e)。还应注意,BE段的弯矩图应向右倾斜,剪力为负值,否则两竖杆的剪力为同方向,不能保持平衡。
(2)图(b)。变形图和弯矩图分别见图(f)、(g)。需要注意的是BC杆应有拐点,B点顺时针旋转,结点B弯矩应保持平衡。BC杆C端弯矩应大于B端,这可以用力矩分配法大致计算一下,Δ引起的固端弯矩为-6iΔ/l,B点转角引起的弯矩为B端4iθ、C端2iθ,两者叠加后可得C端弯矩大一些。
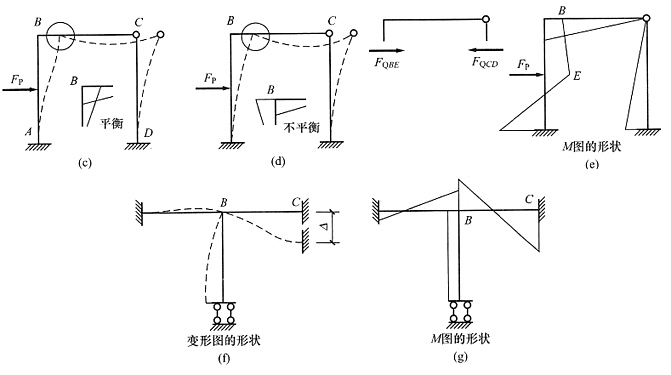
14. 画出下图(a)所示结构内力图(弯矩、剪力、轴力)形状(不要求准确计算);并画出结构变形趋势。EI、EA均为常数,弯矩要求画在构件受拉侧。
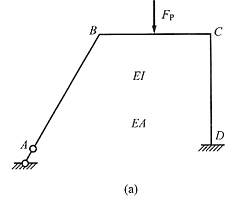
由于A支座反力沿AB杆轴线方向作用,不引起AB杆的弯矩,因此AB杆只有轴力,可以化为图(b)结构并且B支座反力沿图示方向。将B支座反力分解,可见沿x向分量水平朝右,因此水平杆位移向右,结构变形图示于图(b)中。根据变形图的受拉侧可以较容易地画出弯矩图形状,见图(c)。
(2)剪力图根据弯矩图求出,由于弯矩图都是直线,计算很简单。例如,BE段剪力等于两端弯矩差除以长度;正负号判断方法是:从杆轴至弯矩图顺时针旋转时剪力为正,例如BE段剪力为正值,结构剪力图形状见图(d)。
(3)结构轴力图正负号判断如下:由于荷载向下,因此AB杆和CD杆受压,BC杆是根据支座反力的水平分量向右判断出轴力为压力。也可以根据结点的受力平衡,由剪力图求轴力。结构轴力图形状见图(e)。
(4)原结构变形图见图(f),由于各杆EA有限大,所以各杆变形后的投影长度应小于原长。
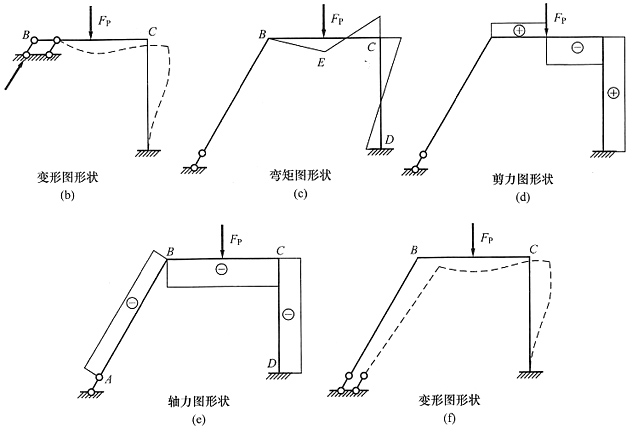
15. 试绘出图(a)所示结构M图和F
Q图的大致形状。各杆抗弯刚度均为EI,且为常数(M<F
Pl/8)。

解 根据外荷载的方向可以判断出A点顺时针旋转,B点逆时针旋转,变形图形状见图(b)。应注意:
(1)AB杆在靠近A端应上凸,这是根据弯矩上侧受拉判断的,判断方法如下:应用力矩分配法的原理,在A、B两点加刚臂,有S
AB=S
AD,在外荷载作用下A点的不平衡力矩为-M-F
Pl/8,分配后的M
AB近似变为(M-F
Pl/8)/2(暂时忽略了B点传递来的弯矩,因此是近似),将已知条件M<F
Pl/8代入前式可得M
AB为负值,上侧受拉,如果再考虑B点传来的弯矩,M
AB应该是增加的。
(2)B点弯矩应注意平衡,在三杆弯矩中M
BA是最大的。
(3)整个结构的弯矩中M
AD最大,也是应用力矩分配法的原理判断。根据变形图画出的M图,如图(c)所示。
剪力图可以由弯矩图确定,直线弯矩图对应的剪力为常数,正负号根据弯矩图的倾斜方向确定,最终剪力图见图(d)。
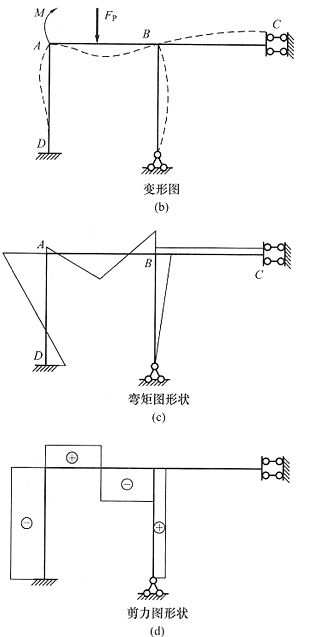
16. 直接绘出图(a)所示结构弯矩图和剪力图的轮廓,不计杆件的轴向变形,除AB杆外EI均为有限值。
解 本题从D点分成左右两个独立的结构,右半部分由于支座F的反力沿杆轴作用,对弯矩无影响,因此可以看作静定部分,弯矩图形状很容易画出,见图(b)。注意:E点有力偶作用,弯矩图应该有突变,但左右两侧弯矩图不平行,是因为E点有支座反力,如果没有该反力,力偶两侧弯矩图应该平行。
再分析D点左侧部分。采用力矩分配法的原理,先大致求一下转动刚度和分配系数,S
CD=3EI/l,S
CB=EI/l(由于AB杆刚度无穷大,所以不弯曲,B点可以沿竖向移动,因此B点相当于CB杆的定向支座),μ
CD=3/4,μ
CB=1/4。再将荷载分成结点力偶和均布力单独作用,在结点力偶作用下,直接画弯矩图,见图(c);在均布荷载下先求出BC杆的固端弯矩(C端固定,B端定向),再按分配系数分配画出弯矩图[见图(d)]。两图叠加并加上右半部分得总弯矩图形状,如图(e)所示。

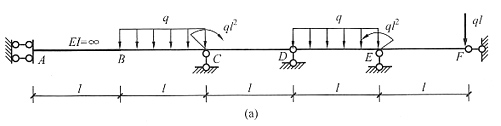
17. 已知图(a)所示三跨连续梁,中间的两个支座分别发生竖向沉降a、b,并且a>b;试根据力学概念绘出弯矩图形状。
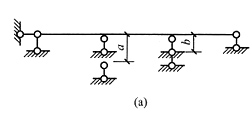
解 先将左支座的沉降分解成b和a-b两部分,结构沉降变成图(b)和图(c)两部分叠加。图(b)沉降量为正对称,支座下移导致杆向下弯曲,弯矩下侧受拉,示于图中。图(c)中先画出变形图用虚线表示,再根据变形图的凸向画出弯矩图。将图(b)和(c)叠加,可以看出B点弯矩是两图相加,C点弯矩两图是相反的,应该相减,但不确定是上侧受拉还是下侧受拉,因为沉降量相差多少不确定。当沉降量a比b大很多时,图(c)中的C点弯矩大于图(b)中的C点弯矩,弯矩图将如图(e)所示,否则将是图(d)。
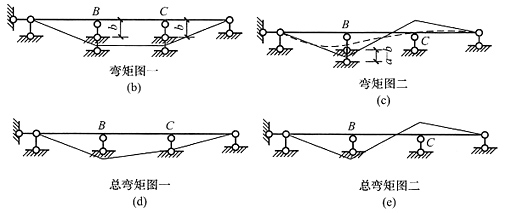
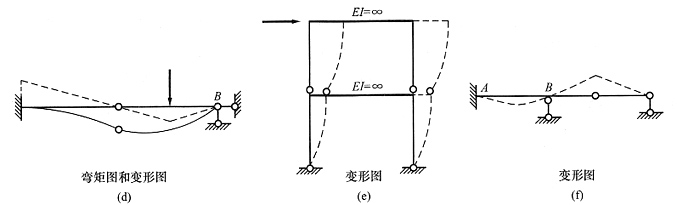
18. 绘制出下图所示结构各杆件的变形示意图。图中未注明杆件的EI=常数。
结构变形图见下图

[解析] 先画下层变形图,竖杆在水平荷载作用下右移,且刚结点顺时针转动,根据水平杆应与竖杆保持垂直的特点,画出水平杆变形图。上层因为水平杆刚度无穷大,所以竖杆上端只平动,不转动,竖杆下端与下层转角保持一致。
19. 定性地画出图(a)、(b)、(c)所示结构在图示荷载(包括广义荷载)作用下变形图的大致形状。
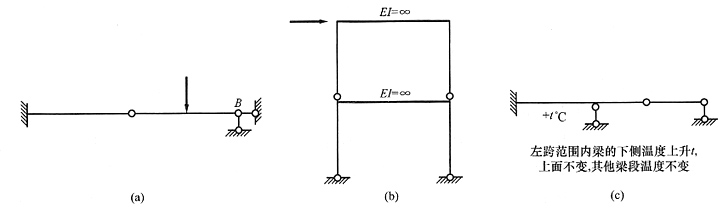
(1)图(a)应当看作静定结构,因为B支座水平反力不引起弯矩,可以去掉,去掉后就变成了静定结构。静定结构应先画弯矩图形状,才能准确判断变形图的弯曲方向。对应的弯矩图和变形图分别见图(d)中的虚线和实线。
(2)图(b)为超静定结构,可以先画变形图。由于上下层柱均有剪力且剪力相等,因此两层柱都有侧移,其中上层侧移为下层的2倍,并且刚结点处无转角(因为横梁刚度无穷大)。最后变形图见图(e)。
(3)图(c)中AB部分为超静定,B点以右为静定部分。本题只有超静定部分产生弯矩,静定部分无荷载,也无温度变化,因此无弯曲。变形图见图(f)。
20. 定性地画出图(a)、(b)所示结构在图示荷载作用下弯矩图的大致形状。
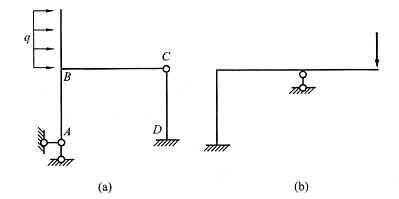
(1)图(a)。先画变形图,在荷载作用下B点右移并顺时针转动,大致的变形图见图(c)。这里需要注意的问题是BA杆和BC杆是否有拐点,这是变形图中的细节问题,要结合弯矩图才能最终作出判断。根据变形图的弯曲侧大致画出弯矩图的形状,见图(d)。从中可以看出A、C两点为铰结点,弯矩为零,AB和BC杆只能单侧受拉,杆中不会出现拐点(拐点是变形曲线的凸向从一侧到另一侧的过渡点,拐点处的弯矩应该等于零),图(c)的变形图是正确的,不需要修正。还有一种可能是AB杆的弯曲变形凸向右侧,对应的弯矩图是右侧受拉,见图(e)、(f)。注意:无论哪种情况,画弯矩图时,与B结点相连的各杆端弯矩竖标都应符合结点B的弯矩平衡。
(2)解图(b)的关键是判断B点是左移还是右移。先画出水平杆的变形图,可知B结点逆时针旋转,则AB杆的B端也应逆时针旋转。又由于荷载和C支座反力沿竖直方向,则它们到AB杆任意一点的力臂是相同的,因此对AB杆的力矩也是相同的,所以AB杆的弯矩是常数。这就要求B点必须左移才能同时保证AB杆逆时针旋转和弯矩为常数这两个条件。最终弯矩图可以根据变形图的弯曲侧画出,变形图和弯矩图分别见图(e)、(f)。还需注意:B点弯矩应保持平衡,因此BC杆有拐点,这一点在变形图中应该准确表达出来。
21. 定性地画出图(a)所示结构在图示荷载作用下弯矩图及变形图的大致形状。
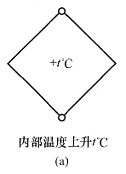
解 本题为正对称,简化半结构见图(b),其中A点y方向的支座是为结构保证几何不变而增加的,反力为零,对内力无影响。可见半结构是静定结构,在温度变化下不产生内力,因此结构的弯矩图为零。变形图见图(d)。画变形图时应注意:C、D两点保持刚结点,各杆由于温度升高应伸长且向内弯曲,变形图应对称。
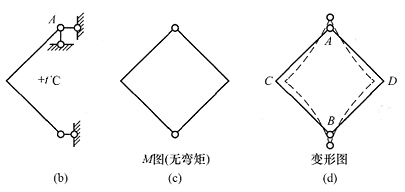
本题所表达的知识点是:超静定结构并不是在温度变化下一定能产生内力,从根本上说,只有变形受到阻碍时才会引起内力,而本题的变形是不受阻碍的,因此不产生内力。
22. 用位移法计算图(a)所示刚架并作M图,各杆EI=常数,其中支座C处弹簧刚度k=6EI/l
3。
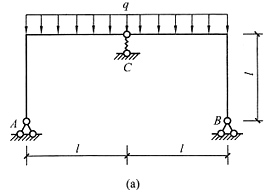
解 本题荷载正对称,先简化半结构见图(b),注意半结构中弹簧刚度应减半。半结构有两个未知量,刚结点转角和弹簧处的线位移,画出基本体系、
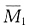
图、
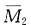
图和M
P图分别见图(c)、(d)、(e)、(f)。位移法方程为
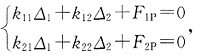
各系数如下:k
11=6EI/l,k
12=k
21=-3EI/l
2,k
22=3EI/l
3+k/2=6EI/l
3,F
1P=-ql
28,F
2P=-3ql/8。代入方程求解得Δ
1=5ql
3/72EI,Δ
2=7ql
4/72EI。
原结构最后的弯矩图见图(g)。
23. 用位移法作图(a)所示结构的弯矩图,并对计算结果进行校核,已知横梁EI=常数,k=EI/l
3。
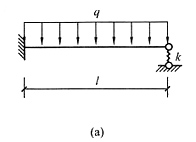
解 本题在弹簧支座处有一个线位移未知量,此处略去,弯矩图见图(b)。下面将重点进行校核,先校核平衡条件,用弹簧支座反力和外荷载对A点取矩,求出
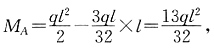
M图中A点的弯矩,可见满足平衡条件。再校核位移条件,校核固定支座处的转角是否等于零。取图(c)的基本结构并施加一虚单位力偶,画出

图,图乘得
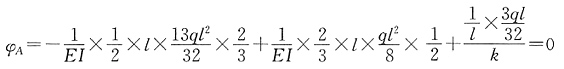
,满足位移条件。所以计算结果正确。
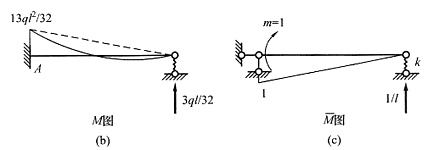
24. 试用位移法绘制图(a)所示结构的弯矩图。已知C点处弹簧刚度系数k=EI/l
3。
解 本题由于CD杆的刚度无穷大,所以C点线位移和转角不独立,因此取两个未知量,B点转角和C点线位移,基本体系见图(b)。画出
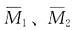
、M
P图,应注意无穷大杆的弯矩必须满足平衡条件,在Δ
2=1时弹簧有变形并产生反力,其余情况弹簧均没有反力。位移法方程为
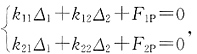
其中k
11=8EI/l,k
12=k
21=-4EI/l
2,k
22=16EI/l
3+k=17EI/l
3,F
1P=0,F
2P=-F
P。代入方程求解得Δ
1=F
Pl
2/30EI,Δ
2=F
Pl
3/15EI。叠加后的原结构弯矩图见图(g)。
25. 用位移法画图(a)所示结构弯矩图。弹簧刚度k=2EI,横梁EI无穷大,柱EI为常数。
解 本题有两个未知量,横梁的水平位移和弹簧支座处的转角,基本体系见图(b),再画出
、M
P图。弹簧对应的转角编号为Δ
1,其只对k
11有影响,将k
11加上k即可。位移法方程为
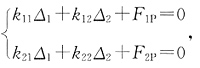
其中k
11=EI+k=3EI,k
12=k
21=-3EI/8,k
22=3EI/8,F
1P=0,F
2P=-F
P。代入方程求解得Δ
1=8F
P/21EI,Δ
2=64F
P/21EI。叠加后的原结构弯矩图见图(f)。
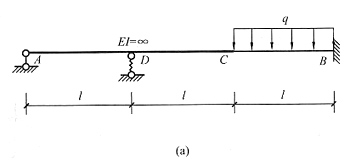
26. 图(a)所示梁CB段的抗弯刚度为EI,而ADC段的抗弯刚度为∞,已知在图示荷载作用下C点竖直向下的线位移为ql
4/(40EI),求作梁的M图,弹簧刚度为k。
解 本题只取一个线位移未知量,在C点加一附加链杆,画出

图和M
P图。注意以下两点:
(1)M
P图中先画CB杆的弯矩图,再将AC两点连成直线,弹簧支座无变形所以反力等于零,对弯矩没有影响。
(2)
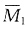
图中支座下移,CB杆相当于两端固定,由C点转角1/2l和竖向单位位移两个因素引起弯矩[见图(c)],先画出CB杆的弯矩;无穷大杆的弯矩按下述方法画出:弹簧支座受到压缩,求出产生的反力,再将AC两点弯矩连成虚线,用分段叠加法叠加上弹簧反力引起的弯矩,由于刚度k没有给出具体数值,因此叠加后D点的弯矩图有上侧受拉和下侧受拉两种情况,图(d)中只画出一种。将Δ
1=ql
4/(40EI)代入公式
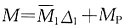
中,可以得到结构的弯矩图,见图(e)或(f)。
27. 图(a)所示连续梁,EI为常数,支座B是弹性抗转支座,抗转刚度为4EI/l,支座C处弹簧刚度为k=3EI/l
3。试用位移法求解,绘制弯矩图。
解 本题有两个未知量,分别是抗转弹簧处的转角和支座C处的线位移,增加约束画出基本体系,见图(b)。
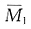
图中,抗转弹簧有反力,支座C处的弹簧受到约束不变形;
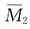
图中C支座弹簧有反力,抗转弹簧不变形;M
P图中两个弹簧均被固定住,均无反力。位移法方程为
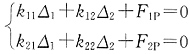
,各系数k
11=4EI/l+4EI/l+4EI/l=12EI/l,k
12=k
21=-6EI/l
2,k
22=12EI/l
3+3EI/l
3=15EI/l
3,F
1P=0,F
2P=-ql/2。代入方程求解得Δ
1=ql
3/48EI,Δ
2=ql
4/24EI。叠加后的原结构弯矩图见图(f)。
28. 用位移法求图(a)所示梁的M图。已知EI=常数,B支座弹簧刚度k=3EI/l
3。
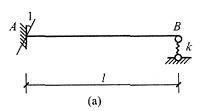
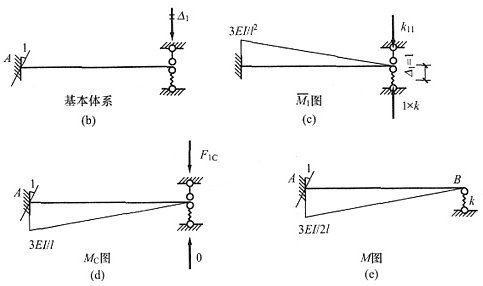
解 B点有一个线位移未知量,画出基本体系见图(b)。
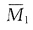
图和M
C图见图(c)、(d)。位移法方程为k
11Δ
1+F
1C=0,k
11=3EI/l
3+k=6EI/l
3,F
1C=-3EI/l
2,代入方程解出Δ
1=l/2。弯矩图见图(e)。
29. 用位移法画图(a)所示结构弯矩图。设k=3EI/l
3 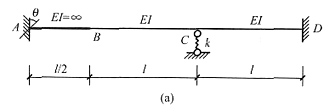
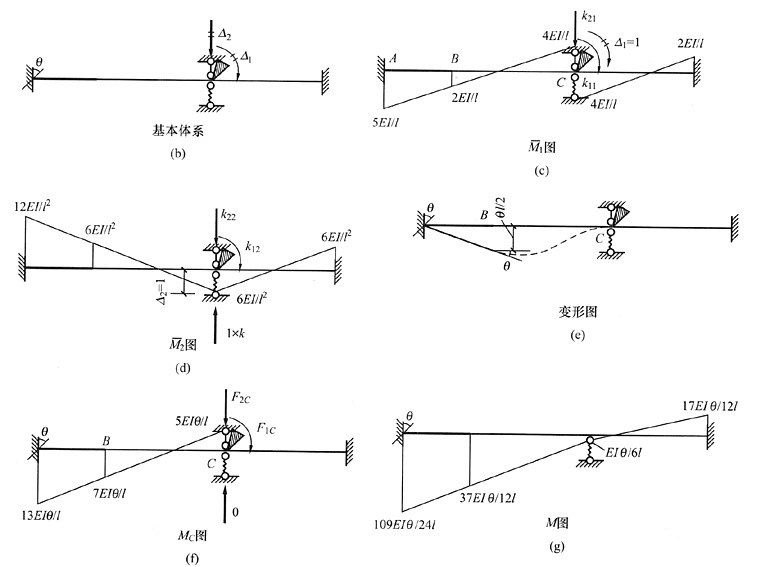
解 本题是无穷大杆、支座位移及弹性支座的综合性题目。先判断未知量,当A支座转动时,AB杆刚体转动,B点有转角和竖向位移,但都与已知位移θ有关,未知量只有C点转角和竖向位移。画
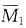
图时应注意,BC杆相当于两端固定,画出其弯矩图后,等斜率延伸至A点就是无穷大杆的弯矩图,这是因为AC杆上无外荷载,因此弯矩图是直线且无折角,其余弯矩图类似。M
C图是由支座转角引起的,先画清楚杆件的变形图,再据此画弯矩图,其中BC杆是两端固定杆在B点转角θ和线位移θl/2下产生弯矩。各系数k
11=8EI/l,k
12=k
21=0,k
22=24EI/l
3+k=27EI/l
3,F
1C=5EIθ/l,F
2C=-12EIθ/l
2。代入位移法方程
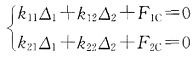
,求解得Δ
1=-5θ/8,Δ
2=4lθ/9。结构弯矩图见图(g)。







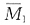 图和MP图见图(c)、(d)。利用公式
图和MP图见图(c)、(d)。利用公式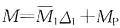 ,并将C点线位移代入Δ1叠加后得结构的弯矩图,见图(e)。
,并将C点线位移代入Δ1叠加后得结构的弯矩图,见图(e)。

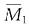 图和MP图[见图(f)、(g)],注意中间竖杆上端水平位移是不受约束的,相当于定向结点(道理同渐进法中的无剪力分配法)。位移法方程k11Δ1+F1P=0,k11=4EI,F1P=7.5,代入方程求解得Δ1=-15/8EI,反对称荷载下的弯矩图见图(h)。将正反对称荷载的弯矩图叠加后得原结构弯矩图,见图(i)。
图和MP图[见图(f)、(g)],注意中间竖杆上端水平位移是不受约束的,相当于定向结点(道理同渐进法中的无剪力分配法)。位移法方程k11Δ1+F1P=0,k11=4EI,F1P=7.5,代入方程求解得Δ1=-15/8EI,反对称荷载下的弯矩图见图(h)。将正反对称荷载的弯矩图叠加后得原结构弯矩图,见图(i)。

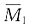 和MP图时BF杆的B端相当于定向结点,MP图中的BF杆弯矩图为两种荷载叠加。位移法方程为k11Δ1+F1P=0,系数k11=2EI,F1P=-6kN·m,解方程得Δ1=3/EI。1/4结构弯矩图见图(g),整个结构弯矩图见图(h)。
和MP图时BF杆的B端相当于定向结点,MP图中的BF杆弯矩图为两种荷载叠加。位移法方程为k11Δ1+F1P=0,系数k11=2EI,F1P=-6kN·m,解方程得Δ1=3/EI。1/4结构弯矩图见图(g),整个结构弯矩图见图(h)。



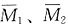 和MP图,
和MP图,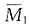 图中AB杆弯矩为两端固定杆在两端同时发生支座转角时产生的弯矩。位移法方程为
图中AB杆弯矩为两端固定杆在两端同时发生支座转角时产生的弯矩。位移法方程为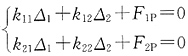 ,求刚度系数和自由项应注意,k11、k12、F1P应等于两个附加刚臂上的力之和,k11=10EI/l,k12=k21=-6EI/l2×2=-12EI/l2,k22=24EI/l3,F1P=0,F2P=-FP。将各系数代入位移法方程并求解,得Δ1=FPl2/8EI,Δ2=5FPl3/48EI。叠加得最后弯矩图见图(g)。
,求刚度系数和自由项应注意,k11、k12、F1P应等于两个附加刚臂上的力之和,k11=10EI/l,k12=k21=-6EI/l2×2=-12EI/l2,k22=24EI/l3,F1P=0,F2P=-FP。将各系数代入位移法方程并求解,得Δ1=FPl2/8EI,Δ2=5FPl3/48EI。叠加得最后弯矩图见图(g)。





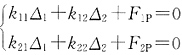 ,
,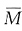 图、
图、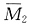 和MP图见图(d)、(f)、(b)。画
和MP图见图(d)、(f)、(b)。画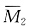 图时,应先弄清楚Δ2=1时结构的变形图[见图(e)],B点左移单位位移至B'点,D点将下移至D'点,且应保证位移后的BD杆沿原方向的投影长度与原长相等,即BB' cosα=DD'sinα,将BB'=1代入求出DD'=4/3,接下来可以继续求出垂直于BD杆的位移分量,该位移分量作为BD两点的相对线位移,将引起BD杆的弯矩。求刚度系数和自由项的过程如下:
图时,应先弄清楚Δ2=1时结构的变形图[见图(e)],B点左移单位位移至B'点,D点将下移至D'点,且应保证位移后的BD杆沿原方向的投影长度与原长相等,即BB' cosα=DD'sinα,将BB'=1代入求出DD'=4/3,接下来可以继续求出垂直于BD杆的位移分量,该位移分量作为BD两点的相对线位移,将引起BD杆的弯矩。求刚度系数和自由项的过程如下: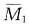 图中B结点力矩平衡可得
图中B结点力矩平衡可得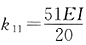 。
。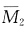 图。由结点B的力矩平衡得是
图。由结点B的力矩平衡得是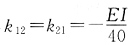 。求k22时,见图(g)。在上图中,由∑MB=0得FRA=0,再由下图,∑MO=0得,k22=109EI/240。
。求k22时,见图(g)。在上图中,由∑MB=0得FRA=0,再由下图,∑MO=0得,k22=109EI/240。





















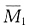 图、
图、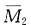 图和MP图分别见图(c)、(d)、(e)、(f)。位移法方程为
图和MP图分别见图(c)、(d)、(e)、(f)。位移法方程为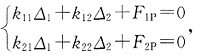 各系数如下:k11=6EI/l,k12=k21=-3EI/l2,k22=3EI/l3+k/2=6EI/l3,F1P=-ql28,F2P=-3ql/8。代入方程求解得Δ1=5ql3/72EI,Δ2=7ql4/72EI。
各系数如下:k11=6EI/l,k12=k21=-3EI/l2,k22=3EI/l3+k/2=6EI/l3,F1P=-ql28,F2P=-3ql/8。代入方程求解得Δ1=5ql3/72EI,Δ2=7ql4/72EI。

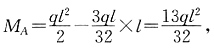 M图中A点的弯矩,可见满足平衡条件。再校核位移条件,校核固定支座处的转角是否等于零。取图(c)的基本结构并施加一虚单位力偶,画出
M图中A点的弯矩,可见满足平衡条件。再校核位移条件,校核固定支座处的转角是否等于零。取图(c)的基本结构并施加一虚单位力偶,画出 图,图乘得
图,图乘得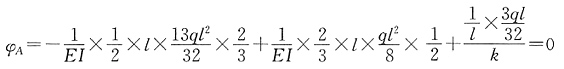 ,满足位移条件。所以计算结果正确。
,满足位移条件。所以计算结果正确。

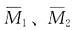 、MP图,应注意无穷大杆的弯矩必须满足平衡条件,在Δ2=1时弹簧有变形并产生反力,其余情况弹簧均没有反力。位移法方程为
、MP图,应注意无穷大杆的弯矩必须满足平衡条件,在Δ2=1时弹簧有变形并产生反力,其余情况弹簧均没有反力。位移法方程为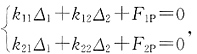 其中k11=8EI/l,k12=k21=-4EI/l2,k22=16EI/l3+k=17EI/l3,F1P=0,F2P=-FP。代入方程求解得Δ1=FPl2/30EI,Δ2=FPl3/15EI。叠加后的原结构弯矩图见图(g)。
其中k11=8EI/l,k12=k21=-4EI/l2,k22=16EI/l3+k=17EI/l3,F1P=0,F2P=-FP。代入方程求解得Δ1=FPl2/30EI,Δ2=FPl3/15EI。叠加后的原结构弯矩图见图(g)。

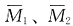 、MP图。弹簧对应的转角编号为Δ1,其只对k11有影响,将k11加上k即可。位移法方程为
、MP图。弹簧对应的转角编号为Δ1,其只对k11有影响,将k11加上k即可。位移法方程为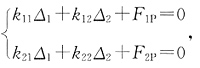 其中k11=EI+k=3EI,k12=k21=-3EI/8,k22=3EI/8,F1P=0,F2P=-FP。代入方程求解得Δ1=8FP/21EI,Δ2=64FP/21EI。叠加后的原结构弯矩图见图(f)。
其中k11=EI+k=3EI,k12=k21=-3EI/8,k22=3EI/8,F1P=0,F2P=-FP。代入方程求解得Δ1=8FP/21EI,Δ2=64FP/21EI。叠加后的原结构弯矩图见图(f)。

 图和MP图。注意以下两点:
图和MP图。注意以下两点: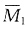 图中支座下移,CB杆相当于两端固定,由C点转角1/2l和竖向单位位移两个因素引起弯矩[见图(c)],先画出CB杆的弯矩;无穷大杆的弯矩按下述方法画出:弹簧支座受到压缩,求出产生的反力,再将AC两点弯矩连成虚线,用分段叠加法叠加上弹簧反力引起的弯矩,由于刚度k没有给出具体数值,因此叠加后D点的弯矩图有上侧受拉和下侧受拉两种情况,图(d)中只画出一种。将Δ1=ql4/(40EI)代入公式
图中支座下移,CB杆相当于两端固定,由C点转角1/2l和竖向单位位移两个因素引起弯矩[见图(c)],先画出CB杆的弯矩;无穷大杆的弯矩按下述方法画出:弹簧支座受到压缩,求出产生的反力,再将AC两点弯矩连成虚线,用分段叠加法叠加上弹簧反力引起的弯矩,由于刚度k没有给出具体数值,因此叠加后D点的弯矩图有上侧受拉和下侧受拉两种情况,图(d)中只画出一种。将Δ1=ql4/(40EI)代入公式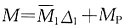 中,可以得到结构的弯矩图,见图(e)或(f)。
中,可以得到结构的弯矩图,见图(e)或(f)。

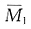 图中,抗转弹簧有反力,支座C处的弹簧受到约束不变形;
图中,抗转弹簧有反力,支座C处的弹簧受到约束不变形;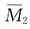 图中C支座弹簧有反力,抗转弹簧不变形;MP图中两个弹簧均被固定住,均无反力。位移法方程为
图中C支座弹簧有反力,抗转弹簧不变形;MP图中两个弹簧均被固定住,均无反力。位移法方程为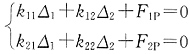 ,各系数k11=4EI/l+4EI/l+4EI/l=12EI/l,k12=k21=-6EI/l2,k22=12EI/l3+3EI/l3=15EI/l3,F1P=0,F2P=-ql/2。代入方程求解得Δ1=ql3/48EI,Δ2=ql4/24EI。叠加后的原结构弯矩图见图(f)。
,各系数k11=4EI/l+4EI/l+4EI/l=12EI/l,k12=k21=-6EI/l2,k22=12EI/l3+3EI/l3=15EI/l3,F1P=0,F2P=-ql/2。代入方程求解得Δ1=ql3/48EI,Δ2=ql4/24EI。叠加后的原结构弯矩图见图(f)。

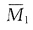 图和MC图见图(c)、(d)。位移法方程为k11Δ1+F1C=0,k11=3EI/l3+k=6EI/l3,F1C=-3EI/l2,代入方程解出Δ1=l/2。弯矩图见图(e)。
图和MC图见图(c)、(d)。位移法方程为k11Δ1+F1C=0,k11=3EI/l3+k=6EI/l3,F1C=-3EI/l2,代入方程解出Δ1=l/2。弯矩图见图(e)。

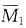 图时应注意,BC杆相当于两端固定,画出其弯矩图后,等斜率延伸至A点就是无穷大杆的弯矩图,这是因为AC杆上无外荷载,因此弯矩图是直线且无折角,其余弯矩图类似。MC图是由支座转角引起的,先画清楚杆件的变形图,再据此画弯矩图,其中BC杆是两端固定杆在B点转角θ和线位移θl/2下产生弯矩。各系数k11=8EI/l,k12=k21=0,k22=24EI/l3+k=27EI/l3,F1C=5EIθ/l,F2C=-12EIθ/l2。代入位移法方程
图时应注意,BC杆相当于两端固定,画出其弯矩图后,等斜率延伸至A点就是无穷大杆的弯矩图,这是因为AC杆上无外荷载,因此弯矩图是直线且无折角,其余弯矩图类似。MC图是由支座转角引起的,先画清楚杆件的变形图,再据此画弯矩图,其中BC杆是两端固定杆在B点转角θ和线位移θl/2下产生弯矩。各系数k11=8EI/l,k12=k21=0,k22=24EI/l3+k=27EI/l3,F1C=5EIθ/l,F2C=-12EIθ/l2。代入位移法方程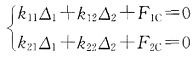 ,求解得Δ1=-5θ/8,Δ2=4lθ/9。结构弯矩图见图(g)。
,求解得Δ1=-5θ/8,Δ2=4lθ/9。结构弯矩图见图(g)。
