一、选择题1. 设函数y=f(x)在点x
0处可导，且下式各极限都存在，其中一定成立的是______
A．
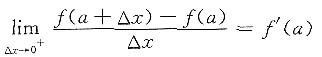
B．
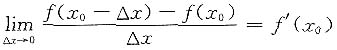
C．
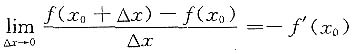
D．
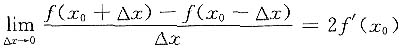
A B C D
D
[解析] 因为
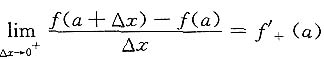
，不一定等于f'(a)，或f'(a)不存在，故A不成立．
对B，
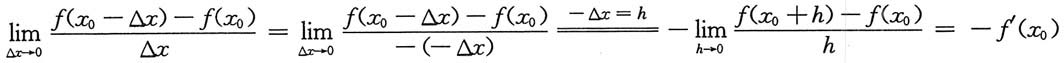
故B不正确．
由定义，知C不成立，故应选D．事实上
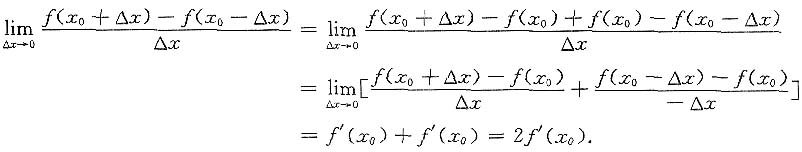
3. 设y=f(x)在x=x
0处可导，且f'(x
0)=-2，则
等于______
A．
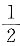
B．2
C．
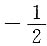
D．-2
A B C D
B
[解析]
=-f'(x
0)=-(-2)=2，故选B．
二、填空题1. 设f(x)在点x=0处可导，且f(0)=0，则
______．
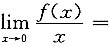
f'(0)
[解析] 因f(0)=0，由导数定义可知，
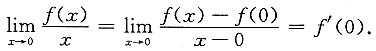
2. 设y=x
e+e
x+lnx+e
e，则y'=______．
3. 设f(x)=2
x，g(x)=x
2，则f'(g'(x))=______．
4xln2．
[解析] f'(x)=2xln2，g'(x)=2x，则f'(g'(x))=22xln2=4xln2．
4. 设
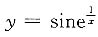
，则
______．
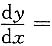
[解析] 用复合函数求导法，
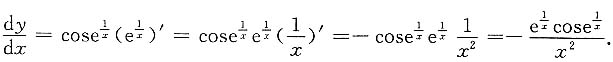
5. 设f'(1)=1，则
=______．
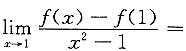
[解析]
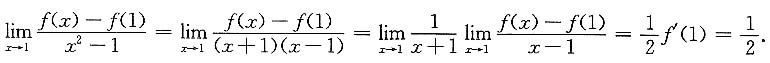
6. 设xy
2-e
xy+2=0，则
______．
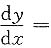
[解析] 利用隐函数求导法，两端对x求导：
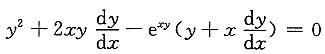
解出
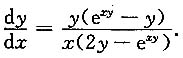
7. 设
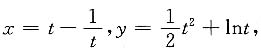
则
______．
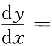
t
[解析] 利用参数方程确定的函数求导法，得
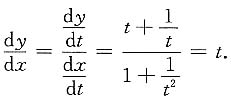
8. 曲线y=x+e
x在点x=0处的切线方程是______，法线方程是______．
y=2x+1，
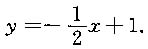
[解析] 设f(x)=x+e
x，则f'(x)=1+e
x，f'(0)=2，又当x=0时，y=1，故切线方程为
y-1=2(x-0)，即y=2x+1．
法线方程为
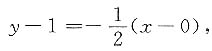
即
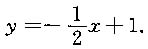
9. 设
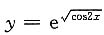
，则dy=______dcos2x．
[解析] 利用一阶微分形式不变性，则
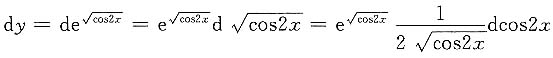
，故填
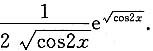
10. 设f'(x
0)=-1，则
______．
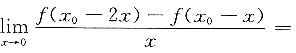
11. 设f(x)=x
2sin(x-1)，则f'(1)=______．
12. 设f(x)=sin(lnx)+ln(sinx)，则f'(x)=______．
13. 已知由方程x
2+y
2=e
y确定函数y=y(x)，则
______．
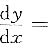
14. 曲线
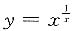
在(1，1)的切线方程是______，法线方程是______．
15. 设f(x)的二阶导数存在，y=ln[f(x)]，则y"=______．
16. 设
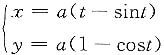
，则
______．
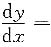
17. 设y=arctane
x4+arctane
-x，则dy=______．
18. 设
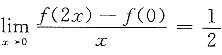
，则f'(0)=______．
19. 设f(x)=2
x，g(x)=x
2，则f'[g'(x)]=______．
20. 由方程xy
2-e
xy+3=0确定的隐函数y=y(x)的导数
______．
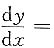
21. 设f(x)=ln(1+x
2)，则f"(-1)=______．
23. 设
，则
______．
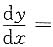
在点x=0处______
在点x=1处连续可导，则a和b的值分别是______
______
，则
______
，则y'=______
在点
处的切线方程是______
深色：已答题 浅色：未答题