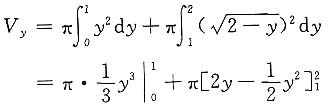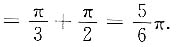银符考试题库B12
现在是：
试卷总分：100.0
您的得分：
考试时间为：
点击“开始答卷”进行答题
交卷
评分
存入我的题库
晒成绩
打印模式
隐藏答案解析
打印
下载
背景
字体
较大
大
中
小
较小
退出
专升本高等数学(一)分类模拟31
一、选择题
1. 函数f(x)在区间[a，b]上连续是f(x)在[a，b]上可积的______
A.充分条件
B.必要条件
C.充分必要条件
D.既非充分又非必要条件
A
B
C
D
A
2. 定积分
是______
A.f(x)的一个原函数
B.f(x)的全体原函数
C.确定的常数
D.任意常数
A
B
C
D
C
3. 变上限积分
是______
A.f(x)的一个原函数
B.f(x)的全体原函数
C.f'(x)的一个原函数
D.f'(x)的全体原函数
A
B
C
D
A
4. 设f(x)是连续函数，
则
等于______
A.0
B.a
C.f(a)
D.不存在
A
B
C
D
C
5.
等于______
A．arcsinx
B．
C．arcsinb-arcsina
D．0
A
B
C
D
D
6. 设
，则I的值______
A．
B．
C．
D．I≥1
A
B
C
D
A
7. 下列积分中能用Newton-Leibniz公式的是______
A．
B．
C．
D．
A
B
C
D
D
8. 下列广义积分中，收敛的是______
A．
B．
C．
D．
A
B
C
D
D
9. 下列广义积分中，错误的是______
A．
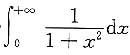
收敛
B．
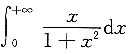
发散
C．
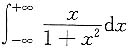
发散
D．
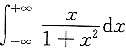
收敛
A
B
C
D
D
10. 设
且f(0)=1，则f(x)等于______
A．
B．
C．
D．e
2x
A
B
C
D
D
二、填空题
1. 由定积分的几何意义，
______．
2. 设
，则
______．
3. 比较积分的大小：
(1)
______
；
(2)
______
；
(3)
______
(1)≤
(2)≥
(3)≥
4. 估计积分的值______＜
＜______．
1，e
5.
______．
0
6.
______，
______．
，π
7. 设
收敛，则P的取值范围是______．
p＜-1
8. 设
收敛，则k的取值范围是______．
k＜-1
9. 设
，则x=______．
-2，3
10.
______．
2
三、解答题
1. 讨论
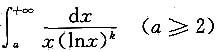
的敛散性．
(1)当k＜1时，
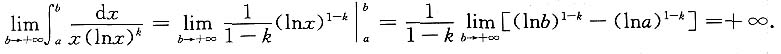
当k=1时，
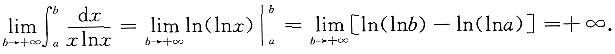
(2)当k＞1时，
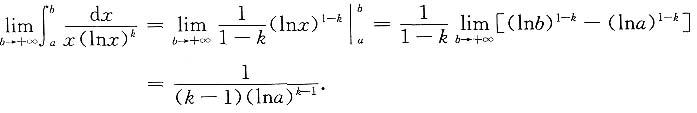
故
当k≤1时，
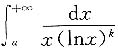
发散；当k＞1时，
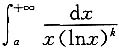
收敛．
2. 计算
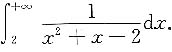
解
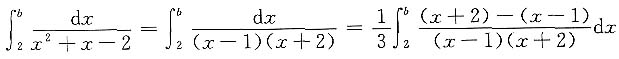
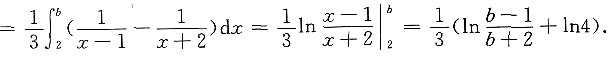
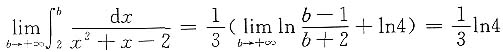
，故
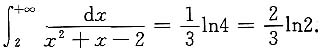
注意 在题中涉及lnx的结果，由于x的积分区间均大于零，我们均去掉了绝对值符号．
3. 讨论
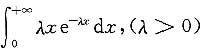
的敛散性．
解 由于
故
因此，
收敛且其广义积分值为
4. 求由抛物线y=1-x
2
与y=x
2
-1所围图形的面积．
解 图形见下图．解联立方程
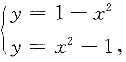
交点为
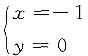
和
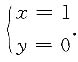
图形面积为
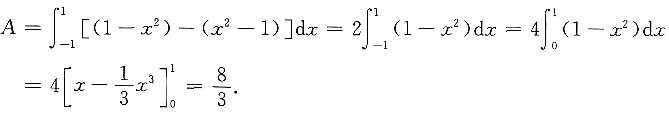
如改为用y作为积分变量，则
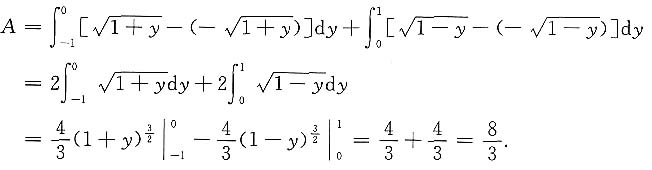
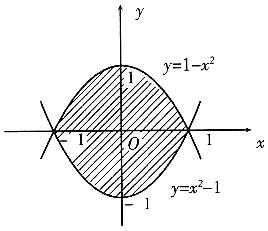
由此看到，选用不同的积分变量计算平面图形的面积，计算的工作量可能不一样．另外，此类问题也可以用二重积分的方法求解，题目为：
计算二重积分
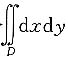
，其中区域D由曲线y=1-x
2
与y=x
2
-1围成．
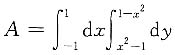
或
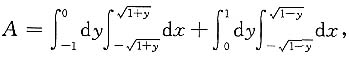
5. 求由抛物线y=4-x
2
与直线x=4，x=0，y=0在区间[0，4]上所围图形的面积．
解 图形见下图，y=4-x
2
与x轴交点为x=2，故
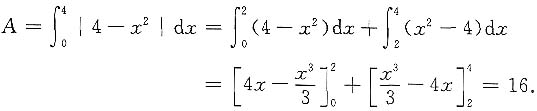
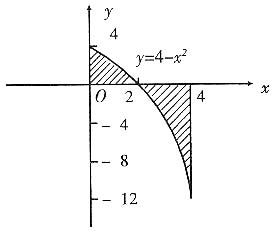
如改为用y作为积分变量，则y=4-x
2
与y轴的交点为(0，4)，与x=4的交点为(4，-12)，故
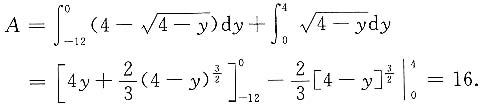
6. 求抛物线y
2
=2x与其在点
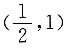
处的法线所围成图形的面积．
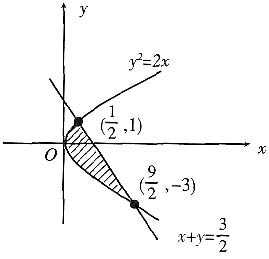
解 图形见下图．y
2
=2x在点
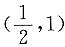
处的切线斜率k
1
为
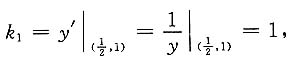
故y
2
=2x在点
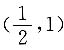
的法线斜率
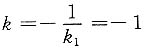
，法线方程为
，
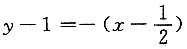
即
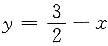
，所求问题转化为求抛物线y
2
=2x与直线
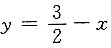
所围图形的面积．
解联立方程
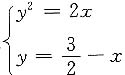
，交点为
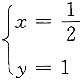
和
，
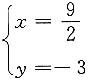
图形面积为
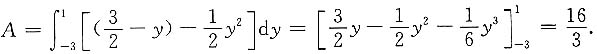
如用x作为积分变量，计算较复杂．
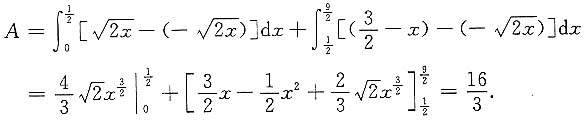
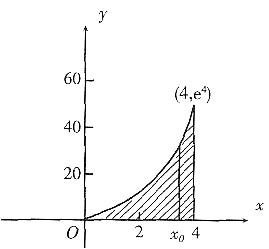
7. 直线x=x
0
平分由曲线y=e
x
与直线x=0，x=4及y=0所围图形的面积，求x
0
．
解 图形见下图．由题意可知
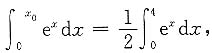
即
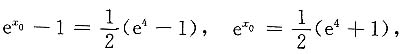
故
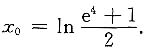
此题也可由
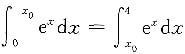
，积分得e
x
0
-1=e
4
-e
x
0
，由此解出
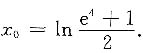
8. 求椭圆
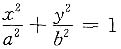
的面积．
解1 利用对称性，得
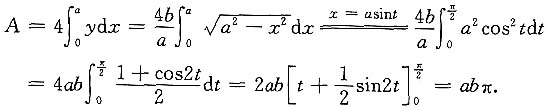
解2 利用椭圆的参数方程
x=cost，y=bsint，则dx=-asintdt．当x=0时，
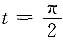
；当x=a时，t=0，故
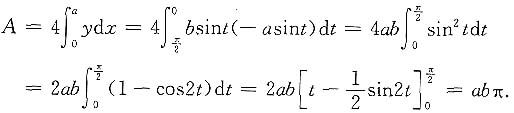
当a=b时，得到圆的面积是a
2
π．
9. 求椭圆
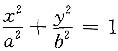
绕x轴旋转一周所生成的旋转体体积．
解1 由
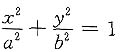
，得
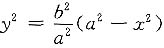
，故旋转体体积
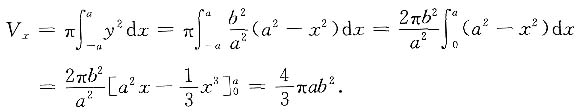
解2 利用椭圆的参数方程
x=acost，y=bsint(0≤t≤π)，则旋转体体积
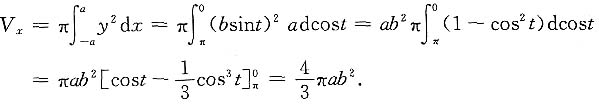
当a=b时，得到球的体积是
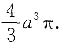
如椭圆绕y轴旋转一周，所生成的旋转体体积为
．
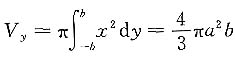
10. 求由抛物线y=2-x
2
与直线y=x(x≥0)x=0围成的平面图形绕x或y轴旋转一周所生成的旋转体体积．
解 图形见下图．解联立方程
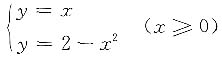
，交点为
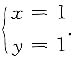
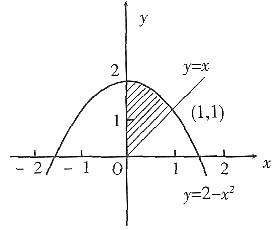
则绕x轴旋转的旋转体体积为,
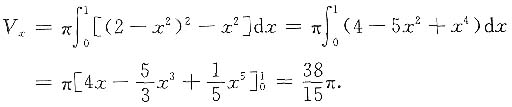
绕y轴旋转的旋转体体积为
一、选择题
1
2
3
4
5
6
7
8
9
10
二、填空题
1
2
3
4
5
6
7
8
9
10
三、解答题
1
2
3
4
5
6
7
8
9
10
深色：已答题 浅色：未答题
提交纠错信息
评价难易度
提交知识点
是______
是______
则
等于______
等于______
，则I的值______
收敛
发散
发散
收敛
且f(0)=1，则f(x)等于______
______．
，则
______．
______
；
______
；
______
＜______．
______．
______，
______．
，π
收敛，则P的取值范围是______．
收敛，则k的取值范围是______．
，则x=______．
______．
的敛散性．
发散；当k＞1时，
收敛．
，故
的敛散性．
收敛且其广义积分值为
和
，其中区域D由曲线y=1-x2与y=x2-1围成．
或
处的法线所围成图形的面积．
处的切线斜率k1为
的法线斜率
，法线方程为
，
，所求问题转化为求抛物线y2=2x与直线
所围图形的面积．
，交点为
和
，
，积分得ex0-1=e4-ex0，由此解出
的面积．
；当x=a时，t=0，故
绕x轴旋转一周所生成的旋转体体积．
，得
，故旋转体体积
．
，交点为
深色：已答题 浅色：未答题