三、解答题1. 求通过点M(1,1,1)且法向量为{4,2,1}的平面方程.
解 由平面的点法式方程有
4(x-1)+2(y-1)+z-1=0,
即
4x+2y+z-7=0.
2. 求过三点A(0,0,0),B(-2,1,3)和C(1,2,4)的平面方程.
解1 设所求平面的法向量为n,由
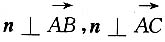
,得到
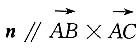
,而
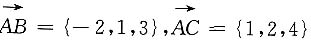
,
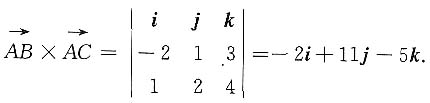
取n={-2,11,-5},由平面的点法式方程,得
-2(x-0)+11(y-0)-5(2-0)=0.
即
2x-11y+5z=0.
解2 因平面方程过原点,由一般式方程知道D=0,故设
Ax+By+Cz=0(A,B,C不全为零)
为所求平面方程.又平面过B,C点,于是
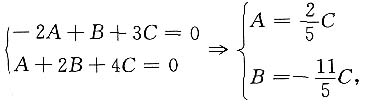
代入所求方程整理并消去C得所求平面方程为
2x-11y+5z=0.
在本题中,A,B,C三个参数有两个是独立的,可解出其中两个参数表示为第三个参数的关系,除将其代入所求平面方程消去第三个参数外,也可将第三个参数取适当值,如取C=5即可.
3. 求过两点A(1,1,1)和B(-1,1,0)且与平面x+y-z=0垂直的平面.
解 设所求平面方程为
A(x-x0)+B(y-y0)+C(z-z0)=0,A,B,C不全为零.
因平面过A点,故
A(x-1)+B(y-1)+C(z-1)=0.
又平面过B点,则
A(-1-1)+B(1-1)+C(0-1)=-2A-C=0.
于是
C=-2A.
又所求平面垂直于平面x+y-z=0,故{A,B,C}⊥(1,1,-1},即
A+B-C=0.
在C=-2A中,取A=1,得C=-2,代入上式得B=-3,所求平面方程为
(x-1)-3(y-1)-2(z-1)=0.
整理得
x-3y-2z+4=0.
4. 求过点M(4,-3,-2)且垂直于两平面x+2y-z=0和2x-3y+4z-5=0的平面方程.
解 设所求平面的法向量为n,因为两平面的法向量分别为n
1={1,2,-1},n
2={2,-3,4},n∥n
1×n
2,
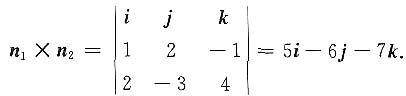
取n={5,-6,-7},又平面过点M(4,-3,-2),由点法式得
5(x-4)-6(y+3)-7(z+2)=0,
整理得
5x-6y-7z-52=0.
5. 确定两平面2x+3y+4z+4=0与2x-3y+4z-4=0的位置关系.
解 因为两平面的法向量分别是n1={2,3,4}和n2={2,-3,4}显然,n1与n2不平行,则两平面不平行也不重合;又n1·n2=2×2+3×(-3)+4×4=11≠0,故两平面不垂直,应为相交但不重合.
6. 两平面3x+by+3z-5=0与ax-6y-z+2=0平行;
解 两平面的法向量分别是n
1={3,b,3}和n
2=(a,-6,-1),由于两平面平行,故n
1∥n
2等价于n
1=λn
2(A是常数).于是
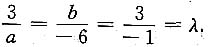
由后一等式,得λ=-3,代入其余等式,得a=-1,b=18.
7. 两平面3x+4y+3z-3=0与ax-6y-z+2=0垂直.
解 两垂直的平面的法向量分别是n1={3,4,3},n2={a,-6,-1},由于,n1⊥n2,故,n1·n2=3a-24-3=0,得a=9.
8. 若平面π过点M(2,-1,5)且与直线l:
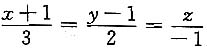
垂直,求π的方程.
解 由于l⊥π,π的法向量可取n={3,2,-1},又π过M点,由点法式得平面方程为
3(x-2)+2(y+1)-(z-5)=0,
整理得
3x+2y-z+1=0.
9. 求过点A(1,2,1)和B(2,4,3)的直线方程.
解 所求直线的方向向量
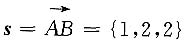
,由直线的点向式方程得
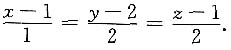
注意 过两定点(x
1,y
1,z
1)和(x
2,y
2,z
2)的两点式方程为
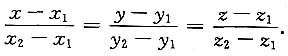
10. 将
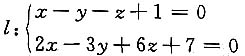
化为标准式方程.
解 设所求直线的方向矢量是s,由两平面的法向量分别是n
1={1,-1,-1)和,n
2={2,-3,6},s∥n
1∥n
2,
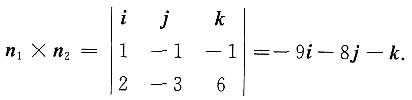
取s={9,8,1},在l上任取一点,令z=0,得方程组
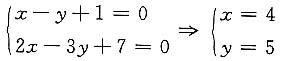
得点(4,5,0).所求标准式方程为
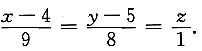
11. 确定直l
1:
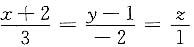
和
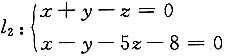
的位置关系.
解 l
1的方向向量s
1={3,-2,1},
l
2的方向向量

,由于-2s
1=s
2,故l
1∥l
2.
12. 求直线l:
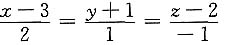
与平面π:x-y-2=0的位置关系.
解 将l化为参数方程
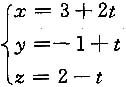
代入平面π,得
3+2t+1-t-2=0
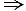
t=-2,
故x=-1,y=-3,z=4,即直线l与平面π相交.
13. 求过点M(1,2,3)且与直线x=2+3t,y=2t,z=-1+t垂直的平面方程.
解 取直线的方向向量s={3,2,1}作为平面的法向量,由点法式即得平面方程为
3(x-1)+2(y-2)+z-3=0.
整理得
3x+2y+z-10=0.
14. 求直线l:
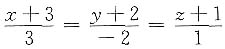
与平面π:x+2y+2z-8=0的交点和夹角.
解 将l化为参数式
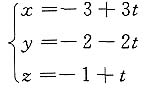
代入π的方程得
-3+3t-2(2+2t)+2(-1+t)-8=0.
解出t=17,从而交点坐标为x=-3+3×17=48,y=-2-2×17=-36,z=-1+17=16,即l与π的交点为(48,-36,16).
l的方向向量
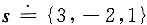
,π的法向量n={1,2,2},设φ为l与π的夹角,则
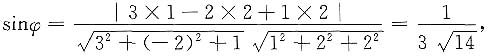
故
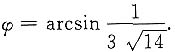
15. 求球面x
2+y
2+z
2+2x-8y+6z+1=0的球心和半径.
解 因x2+y2+z2+2x-8y+6z+1=(x+1)2+(y-4)2+(z+3)2-1-16-9+1=0,故
(x+1)2+(y-4)2+(x+3)2=52
球心坐标(-1,4,-3),半径为5.
16. 一球面过点A(0,0,0),B(1,-1,1),C(1,2,-1)和D(2,3,0),求球面方程.
解 设球面方程为
x
2+y
2+z
2+ax+by+cz+d=0
因B,C,D,A点的坐标满足上述方程,代入得
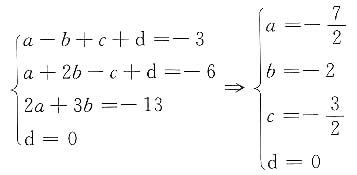
所求球面方程为
2x
2+2y
2+2z
2-7x-4y-3z=0
也可化为标准形式
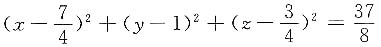
若设所求球面方程为(x-a)
2+(y-b)
2+(z-c)
2=r
2,也可求出所求球面方程,略.
17. 指出下列方程在空间直角坐标系下所表示的曲面.
(1)
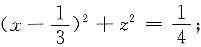
(2)4x
2+9z
2=36;
(3)4x
2+9y
2+16z
2=36;
(4)4x
2-9z
2=36;
(5)x
2+y
2-2z=0;
(6)z
2=x
2+y
2;
(7)2x
2+y
2+z
2=1;
(8)z=1-y
2.
解 (1)母线平行于y轴,准线为
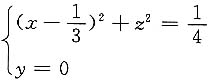
的圆柱面.
缺一变数的方程一般都表示一柱面(x
2+y
2=0表示直线).反之不一定成立.
(2),(4),(8)均为柱面:(2)是椭圆柱面,(4)是双曲柱面,(8)是抛物柱面.
(3),(7)是椭球面.
(5)可看作曲线
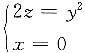
绕z轴旋转一周而成的旋转抛物面,也可看作曲线
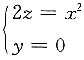
绕x轴旋转一周而成.
(6)可看作直线
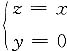
或
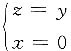
绕z轴旋转而成的锥面.
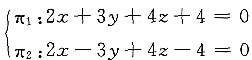 的位置关系是______
的位置关系是______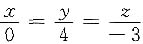 ,则该直线必定______
,则该直线必定______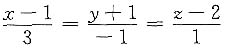 的位置关系是______
的位置关系是______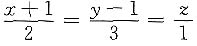 的平面方程是______
的平面方程是______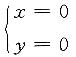 表示______.
表示______.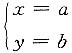 表示______.
表示______.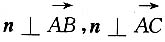 ,得到
,得到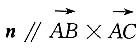 ,而
,而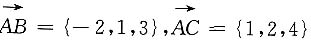 ,
,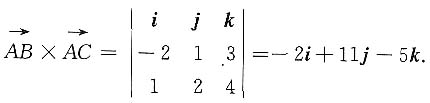
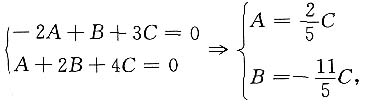
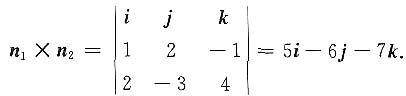
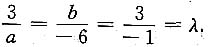
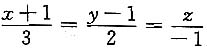 垂直,求π的方程.
垂直,求π的方程.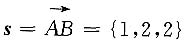 ,由直线的点向式方程得
,由直线的点向式方程得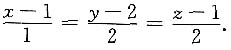
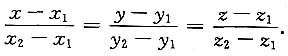
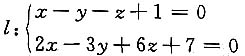 化为标准式方程.
化为标准式方程.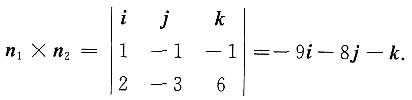
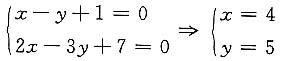
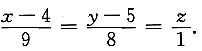
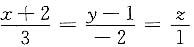 和
和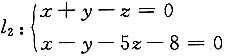 的位置关系.
的位置关系. ,由于-2s1=s2,故l1∥l2.
,由于-2s1=s2,故l1∥l2.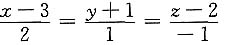 与平面π:x-y-2=0的位置关系.
与平面π:x-y-2=0的位置关系.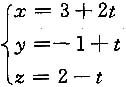 代入平面π,得
代入平面π,得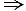 t=-2,
t=-2,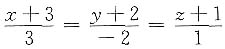 与平面π:x+2y+2z-8=0的交点和夹角.
与平面π:x+2y+2z-8=0的交点和夹角.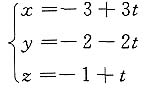 代入π的方程得
代入π的方程得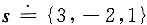 ,π的法向量n={1,2,2},设φ为l与π的夹角,则
,π的法向量n={1,2,2},设φ为l与π的夹角,则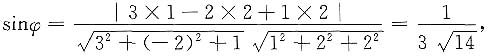
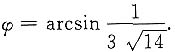
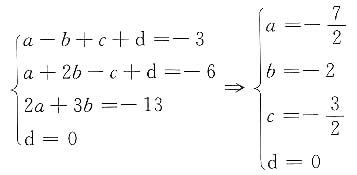
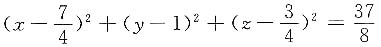
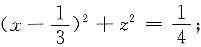
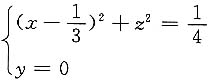 的圆柱面.
的圆柱面.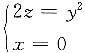 绕z轴旋转一周而成的旋转抛物面,也可看作曲线
绕z轴旋转一周而成的旋转抛物面,也可看作曲线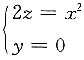 绕x轴旋转一周而成.
绕x轴旋转一周而成.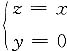 或
或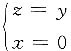 绕z轴旋转而成的锥面.
绕z轴旋转而成的锥面.