一、逻辑推理题下列每题给出的A、B、C、D、E五个选项中,只有一个选项符合试题要求。
二、数学单项选择题下列每题给出的A、B、C、D四个选项中,只有一个选项符合试题要求。
1. 设
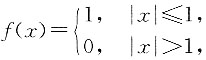
则f{f[f(x)]}=______.
A.
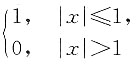
B.
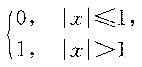
C.0
D.1
A B C D
D
[解析] 由复合函数的定义,
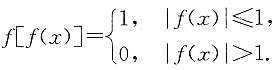
由题意知|f(x)|≤1,因此f[f(x)]=1,故f{f[f(x)]}=1.
复合函数的解析式问题需要按照定义进行处理,尤其是分段函数的复合函数.
2. 当x→0时,下列无穷小中,______是比其他三个更高阶的无穷小?
A.x
2 B.
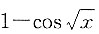
C.
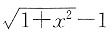
D.x-tan x
A B C D
D
[解析] 由

,而
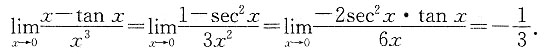
故x-tan x与x
3同阶,所以选D项.
本题考查无穷小量阶的比较,无穷小量阶的比较题型分类较多,但万变不离其宗,方法上要大体抓住阶的定义,利用界限的方式进行处理.另外,要记住常见的几组等价无穷小量公式.如果能够熟练运用Taylor公式,对处理此类问题大有裨益.如本题中

3. 设函数f(x)在区间(-1,1)内有定义,且恒有|f(x)|≤ln(1+x
2),则x=0是f(x)的______.
- A.间断点
- B.连续但不可导点
- C.可导点,且f'(0)=0
- D.可导点,但f'(0)≠0
A B C D
C
[解析] 显然,f(0)=0,而0≤|f(x)|≤ln(1+x
2),又
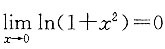
,由夹逼准则知,
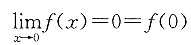
,故f(x)在x=0处连续.另外,
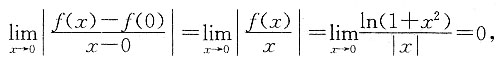
故f(x)在x=0处可导,且f'(0)=0.
抽象函数的连续性与可导性讨论需要利用定义(极限)的方法.
4. 设
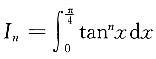
,若n≥2,则I
n+I
n-2=______.
A.
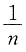
B.
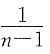
C.
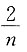
D.
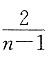
A B C D
B
[解析]
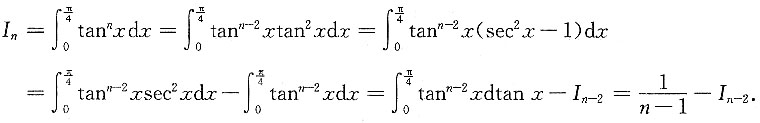
因此,
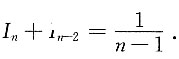
5. 设y=f(x)是区间[0,4]上的可导函数,f(0)=l,f'(x)的图形如下图所示,其中三块图形的面积分别为S
1=1,S
2=5,
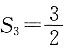
,则f(x)在[0,4]上______.
A.最大值为4,最小值为
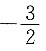
B.最大值为4,最小值为-1
C.最大值为5,最小值为-1
D.最大值为5,最小值为0
A B C D
D
[解析] 由牛顿-莱布尼茨公式及定积分几何意义知,

由f(x)在区间[0,4]上连续,故
f
max=max{f(0),f(1),f(3),f(4)}=5.
f
min=min{f(0),f(1),f(3),f(4)}=0.
第一,曲边梯形的面积问题可以归结为定积分问题,这正是定积分的几何意义所在;第二,连续函数在闭区间上的最值可以归结为端点值、内部驻点值、内部不可导点值的最大值.
6. 若函数f,g均可微,设z=f[xy,ln x+g(xy)],则
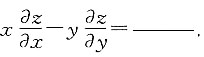
A.
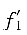
B.

C.0
D.1
A B C D
B
[解析]
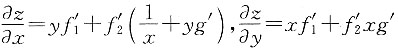
,故
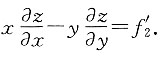
7. 设α
1,α
2,α
3线性无关,则下列向量组线性相关的是______.
- A.α1-2α2,α2-2α3,α3-2α1
- B.α1+2α2,α2+2α3,α3+2α1
- C.α1+α2,α2+α3
- D.α1+α3,α1-α2,3α1-2α2+α3
A B C D
D
[解析]
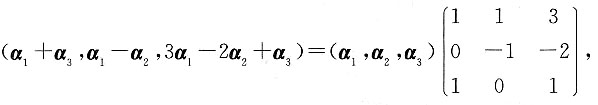
而矩阵
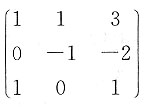
不可逆,故α
1+α
3,α
1-α
2,3α
1-2α
2+α
3线性相关.
类似地,可以说明其他选项的向量线性无关.
本题用到一个非常重要的判定线性相关(无关)的方法:
设向量组α
1,…,α
r线性无关,向量组β
1,…,β
s可由α
1,…,α
t线性表示,即存在P=(c
ij)
t×s,使
(β
1,…,β
s)=(α
1,…,α
r)P,
则:①r(β
1,…,β
s)=r(P);
②当t=s时,β
1,…,β
s线性无关
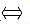
|P|≠0.
10. 设随机变量X的密度函数为f(x),且f(x)为偶函数,X的分布函数为F(x),则对任意实数a,有______.
A.
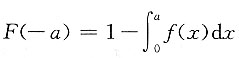
B.
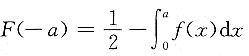
C.F(-a)=F(a)
D.F(-a)=2F(a)-1
A B C D
B
[解析]
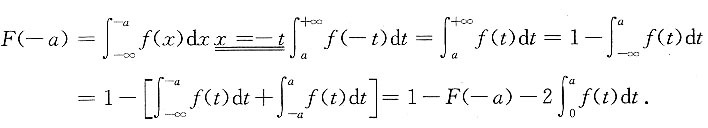
故应选B.
三、数学计算题1. 求极限
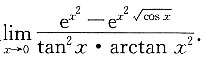
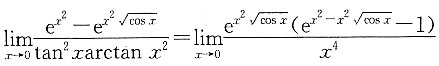
,而
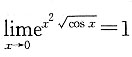
及
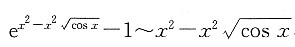
,故

这是
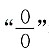
型不定式,利用洛必达法则,得

计算极限要先观察其特征,尽量先等价替换,化简极限,再观察是否能够使用洛必达法则.值得一提的是,提取因子变加减为乘积再等价替换的思想在极限计算中经常遇到.
2. 求不定积分
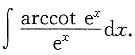
3. 设
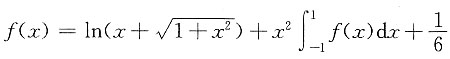
,求f(x).
定积分是一个数,于是设
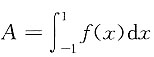
,等式两边积分得
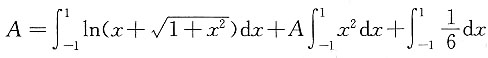
,注意到
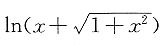
为一个奇函数,故
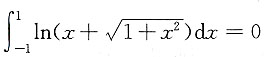
,故
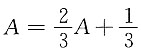
,因此,A=1,
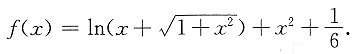
此类题型可以看作积分方程的问题,积分方程大体可以分为两大类:一类是定积分方程,处理此类问题的方法是两边积分法;二是变上限积分方程,处理此类问题的方法是两边求导法.
4. 使利润最大的x,y和最大利润;
这是一个极值问题.
由
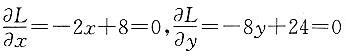
,得x=4,y=3.
即点(4,3)为L(x,y)唯一可能取到极值的点,由该问题最大值一定存在,可知
L
max=L(4,3)=37(万元).
5. 如果原料降至12000千克,求这时利润最大的产量和最大利润.
这是一个条件极值问题,因为2000x+2000y≤12000,即x+y≤6,设拉格朗日函数为
F(x,y,λ)]=-x
2-4y
2+8x+24y-15+λ(x+y-6).
由
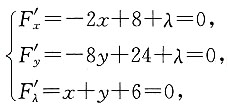
得x=3.2,y=2.8.
同样,由该问题的实际意思知,最大值一定存在,且一定在唯一可能的极值点(3.2,2.8)
处取到,故最大值L(3.2,2.8)=36.2.
计算极值问题一定要看清其是否带有约束条件.

7. 求f(x,y)及f'y(x,y).
由第1小题可得
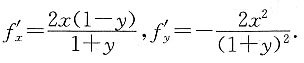
本题第二问也可以采用两边求偏导的方法,这样会更便捷.
8. 有甲、乙两个口袋,两袋中都是3个白球、2个黑球,现从甲袋中任取一球放入乙袋,再从乙袋中任取4个球,设4个球中的黑球数用X表示,求X的分布律.
设A={从甲袋中取出黑球},X的可能取值为0,1,2,3,令{X=i}=B
i,i=0,1,2,3,则
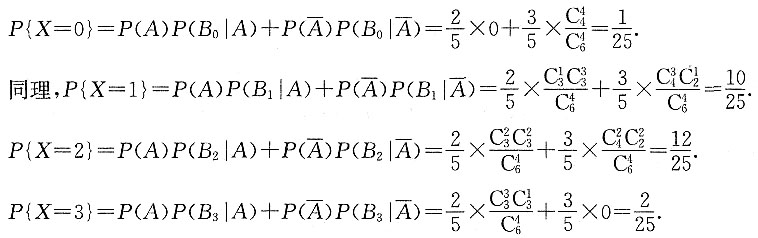
所以X的分布律
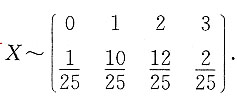
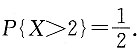
9. 求μ;
由X~N(μ,σ
2),故
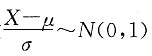
,所以,
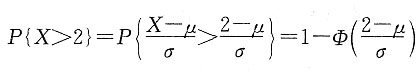
,因此
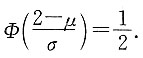
又由于
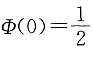
,知μ=2.
10. 已知P{X<0}=0.2,求P{0<x<4}.
依题意,
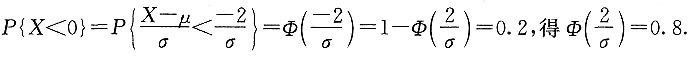
故
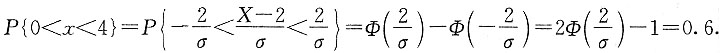
与正态分布相关的问题的一个重要思路是标准化,标准化方便计算.
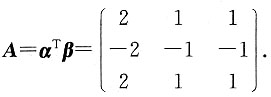
求:11. βα
T;
因为
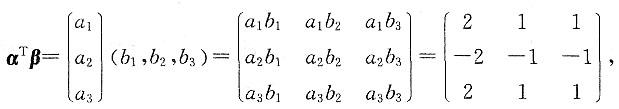
所以
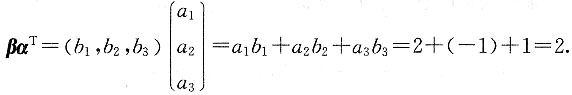
12. A
n.
An=αT(βαT)n-1β=2n-1αTβ=2n-1A.
在矩阵运算问题中,行向量乘以列向量为一个数,列向量乘以行向量为一个矩阵,要注意区分.
13. 设α
1,α
2,α
3是齐次方程组Ax=0的一个基础解系,
β
1=2α
1+α
2,β
2=2α
2+α
3,β
3=2α
3+α
1,
证明:β
1,β
2,β
3也是Ax=0的一个基础解系.
[证明] 首先,Aβ
1=A(2α
1+α
2)=2Aα
1+Aα
2=0,故β
1是Ax=0的解.
同理,β
2,β
3也是Ax=0的解.以下证β
1,β
2,β
3线性无关.
设k
1β
1+k
2β
2+k
3β
3=0,得:
(2k
1+k
3)α
1+(k
1+2k
2)α
2+(k
2+2k
3)α
3=0.
由α
1,α
2,α
3线性无关,知
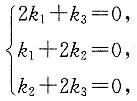
解得k
1=k
2=k
3=0.
故β
1,β
2,β
3线性无关,从而是Ax=0的一个基础解系.
齐次线性方程组的基础解系必须满足以下三条:①均是方程组的解;②线性无关;③个数必须是n-r(A)个.
四、写作题其中论证有效性分析20分,论说文20分。
1. 论证有效性分析:分析下述论证中存在的缺陷和漏洞,选择若干要点,写一篇600字左右的文章,对该论证的有效性进行分析和评论。(论证有效性分析的一般要点是:概念特别是核心概念的界定和使用是否准确并前后一致,有无各种明显的逻辑错误,论证的论据是否成立并支持结论,结论成立的条件是否充分等。要注意分析的内容深度、逻辑结构和语言表达等)
北京市发改委昨日发布消息,5月1日起,北京居民水价、非居民水价和特殊行业水价将同时进行调整。居民阶梯水价按照提交听证会的方案二执行,即第一阶梯户年用水量不超过180立方米,每立方米水价为5元;第二阶梯户年用水量在181~260立方米之间,每立方米水价为7元;第三阶梯户年用水量为260立方米以上,每立方米水价为9元。
4月2日,北京公布水价调整方案,在现行每吨4元的基础上,提出拟上调0.95元或1元两个方案。两套方案均设置了阶梯水价,根据用水量的不同,两套方案水价分别为4.95元、7元、9元以及5元、7元、9元。
4月17日,在居民用水价格调整听证会上,25位听证代表均同意实施居民用水价格调整,其中6人同意方案一,即第一阶梯户年用水量不超过145立方米,每立方米水价为4.95元;17人同意方案二,即第一阶梯户年用水量不超过180立方米,每立方米水价为5元。另有2人提出了新的方案。
为何会选择方案二?北京市发展改革委委员李素芳说:“调价将保基本,区分基本需求和非基本需求,用水越多付费越多,促进用水大户节约用水。”通过适度调整水价,优先保障水资源费、排水成本,促进水资源的节约,也为社会成本进入排水行业创造一定条件。水费负担将增加多少?记者随机采访几位普通市民,他们表示支持阶梯水价,每月增加的水费是可以承担的。家住北京市东城区交道口的王女士说,一家三口一个月用水15吨左右,一年用水180吨,自己算比较节省的,洗菜、洗漱后的水都用来冲厕所,按照方案一属于第二阶梯用户。
北京市发展改革委成本调查队对供排水成本进行了监审。在供水成本方面,2012年,北京市属企业供水成本为每立方米3.08元,而现行居民自来水费为1.7元。在排水成本方面,2012年市属企业排水成本为每立方米1.7元,而现行居民用水污水处理费为1.04元。在水资源费方面,根据2013年国家对各地区水资源费调整文件的要求,北京市水资源费平均征收标准应不低于每立方米1.6元,而现行居民用水水资源费为1.26元。这样计算,北京市总的用水成本为每立方米6.38元,如果考虑供水企业需缴纳增值税等影响,含税成本为每立方米6.59元。
目前,全国普遍存在自来水厂亏损运营的状况,北京的相关企业情况亦堪忧。业内人士表示,水价长期较低,根本体现不了水资源的紧张状况,更无法支撑自来水、排水等企业的发展和设备更新。实行阶梯水价,将有助于解决一部分情况。
[参考范文] 缺乏说服力的论证
原文通过一系列材料和推理,论述了北京市水价调整的合理性,但其论证过程却存在诸多不足之处,具体分析如下。
首先,“25位听证代表均同意实施居民用水价格调整”这一论断值得商榷。25位听证代表的意见是否具有普遍代表性?他们是谁?来自哪里?25代表的数量是否足够?如果答案为否,那么该论断与实际情况可能存在较大偏差,因此无法有效地得出居民同意水价调整的提案。
其次,从记者给出的调查结果可以看出,在非常节省的情况下,一年用水约180吨。以此计算,就一年水费来说,方案二只比方案一的费用差0.25元,两种方案的实际差异不大,可见实质上并无选择的必要。
再次,供水企业成本高,不一定要提高水的价格。造成水厂亏损运营的原因可能是多方面的,比如企业效率、管理机制等。针对具体的原因,只有实施有效的解决方法与途径,才能从根本上解决问题。如果深层问题得不到解决,即使提高水价,可能也无法扭转亏损的局面。甚至由于这种单科归因的思想,不深入研究解决,从而无法避免问题。
最后,业内人士的理由有些偏颇,以水价高低来体现水资源的紧张状况有待商榷。自来水、排水等企业的发展和设备更新,也是一个长期的任务,需要多方面的统筹,不能仅以基础水价来调整,从而作为调整的有力论据。现在很多制水卖水企业,效益与发展很好,值得这些业内人士思考。
原论证中虽然还存在其他不足之处,但仅以上述分析已经足以说明该论证的缺陷,其论述难以令人信服。
2. 论说文:根据下述材料,写一篇700字左右的论说文,题目自拟。
“水至清则无鱼,人至察则无徒”这句话,源于《大戴礼记·子张问入官》,后人多用此告诫人们指责人不要太苛刻,看问题不要过于严厉,否则,就容易使大家因害怕而不愿意与之打交道,就像水过于清澈养不住鱼儿一样。但是,实际中总有一些人在“创新”地应用:凡事不必认真。得饶人处且饶人,甚至见了危害人们利益的人或事,也睁一只眼闭一只眼。企业管理中,也常见这样的情况:我知道啊,反正没什么大损失,他可是我的干将,差不多就得了。
[参考范文] 水清鱼更多
古语云:“水至清则无鱼,人至察则无徒。”本意是好的,但现今某些人对它的创新性误用,则危害甚大,尤其是对企业的生存与发展来说。我认为,企业要良性发展,要做到基业长青,就要正本清源,要做到“水至清”。
合抱之木,生于毫末;九层之台,起于累土。再大型的企业,也是由基本的微小事物组成;再伟大的事业,也是由细小的单元组成;再优秀的管理,也是由具体的流程组成。每个单元、每个细节做好了,才能保证整体目标的有效实现。“细节决定成败”,也正说明了这些“微末之处”的重要性。
而在实际的企业管理中,“犯了小错,反正没什么大损失,就算了吧”的情况很常见。殊不知,“千里之堤,溃于蚁穴”。这种漠视微小不足的行为是很危险的。业务或行为上小的过失,如果不能及时纠正,可能会变成影响整个项目,乃至整个企业的危险因素。三鹿奶粉倒闭,起于第一次加有害物质而不察;冠生园倒闭,源于第一次欺骗消费者的行为而不纠。再小的过失与缺陷,也要得到根本的纠正,切莫让它发展为“危害大坝的蚁穴”。
另外,企业对某个人或某个部门的细小过失的不察,会影响其他人的行为,甚至会形成错误的行为准则。就考勤来说,王五迟到了,而领导认为他辛苦了,迟到一会儿可以原谅,那么张三、李四也感觉自己辛苦了,则要怎样处理呢?当辛苦成为迟到的理由时,考勤制度几乎就等同于虚设了。其他事情亦是如此。所以,再小的过失也要得到根本的纠正,不让它成为“坏的榜样”。
再者,如果出现小的过失而不从根本上纠正,或者由于各种借口理由而忽略,那么当类似的过失出现时再纠正,可能会产生因同一性质的问题不公平的对待,而出现负面情绪的情况。这也可能会对企业的发展产生不良影响。
可见,对任何违反企业制度或行为规范的过失,都要从根本上进行纠正。只有正本清源,才能确保企业的长远、良性发展。
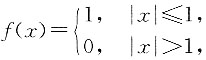 则f{f[f(x)]}=______.
则f{f[f(x)]}=______.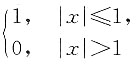
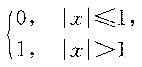
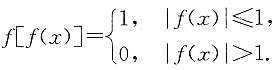
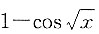
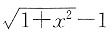
 ,而
,而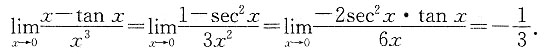

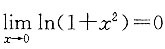 ,由夹逼准则知,
,由夹逼准则知,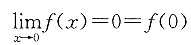 ,故f(x)在x=0处连续.另外,
,故f(x)在x=0处连续.另外,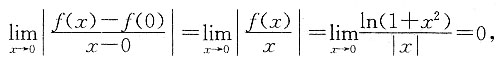
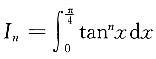 ,若n≥2,则In+In-2=______.
,若n≥2,则In+In-2=______.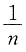
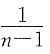
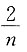
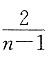
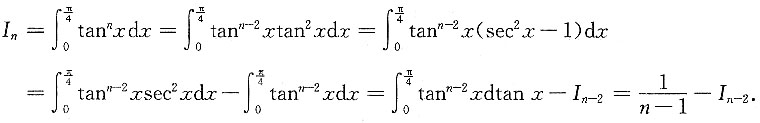
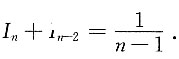
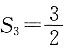 ,则f(x)在[0,4]上______.
,则f(x)在[0,4]上______.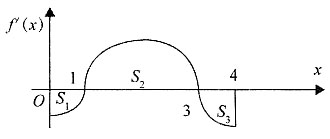
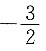

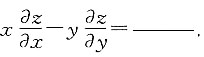
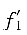

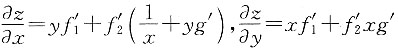 ,故
,故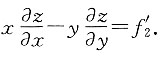
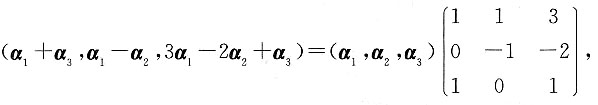
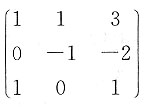 不可逆,故α1+α3,α1-α2,3α1-2α2+α3线性相关.
不可逆,故α1+α3,α1-α2,3α1-2α2+α3线性相关.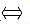 |P|≠0.
|P|≠0.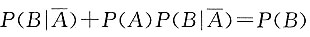
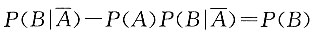
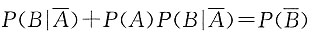
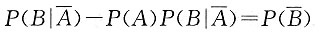
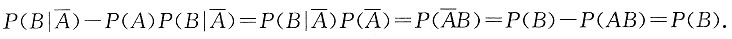
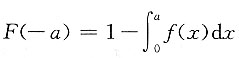
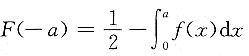
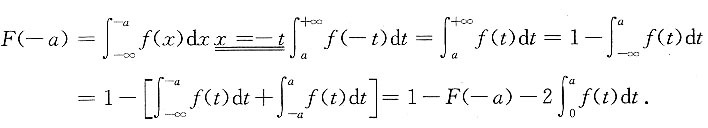
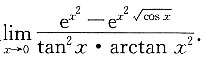
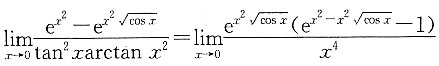 ,而
,而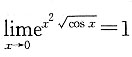 及
及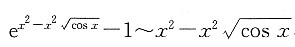 ,故
,故
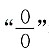 型不定式,利用洛必达法则,得
型不定式,利用洛必达法则,得
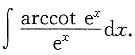
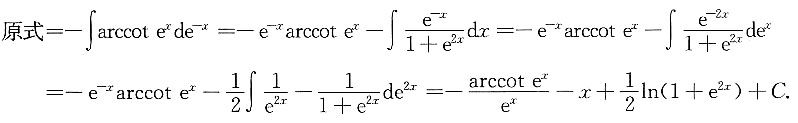
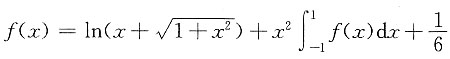 ,求f(x).
,求f(x).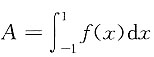 ,等式两边积分得
,等式两边积分得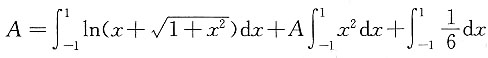 ,注意到
,注意到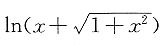 为一个奇函数,故
为一个奇函数,故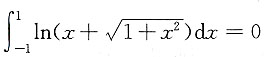 ,故
,故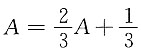 ,因此,A=1,
,因此,A=1,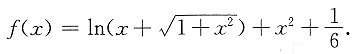
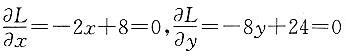 ,得x=4,y=3.
,得x=4,y=3.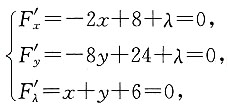 得x=3.2,y=2.8.
得x=3.2,y=2.8.
 ,则
,则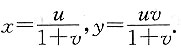
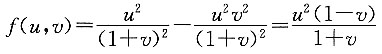 ,即
,即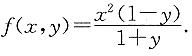
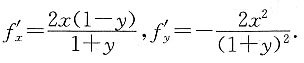
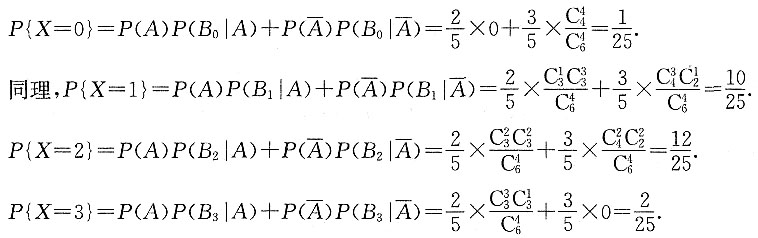
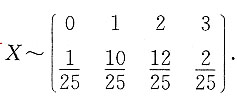
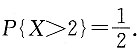
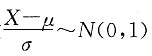 ,所以,
,所以,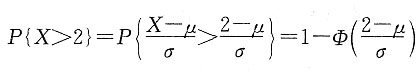 ,因此
,因此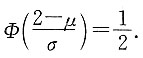
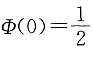 ,知μ=2.
,知μ=2.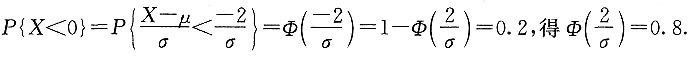
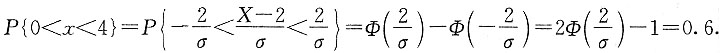
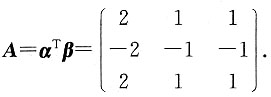
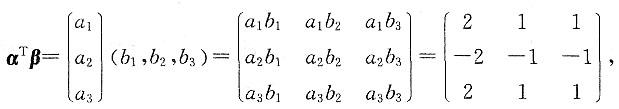
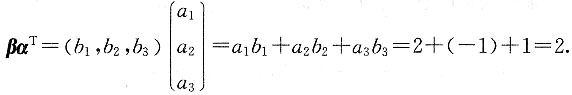
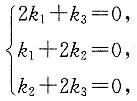 解得k1=k2=k3=0.
解得k1=k2=k3=0.