一、逻辑推理题下列每题给出的A、B、C、D、E五个选项中,只有一个选项符合试题要求。
赵亮:和古代奥运会不同,现代奥运会允许专业运动员和业余运动员一起比赛。专业运动员一般都有业余运动员所缺少的物质和技术资源,特别是有些专业运动员是由国家直接培养的,这使得专业运动员和业余运动员之间的比赛事实上不平等。因此,允许专业运动员参加比赛违反奥运会的平等原则,不符合奥林匹克精神。
王宜:现代奥运会的精神是向更高的体育竞赛纪录冲击,不管此种纪录是专业或是业余运动员创造的。因此,不允许专业运动员参加奥林匹克比赛是没有道理的。 二、数学单项选择题下列每题给出的A、B、C、D四个选项中,只有一个选项符合试题要求。
2. 设x
nsin x是f(x)的一个原函数,
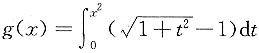
,若x→0时,f(x)与g(x)是同阶无穷小,则n=______.
A B C D
D
[解析] 因为x
nsin x是f(x)的一个原函数,则可得到f(x)=nx
n-1sin x+x
ncos x,当x→0时,(n+1)x
n是f(x)的等价无穷小,则由洛必达法则可得
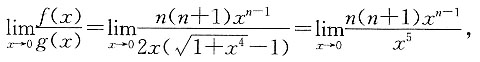
又因为当x→0时,f(x)与g(x)是同阶无穷小,故n=6.
4. 曲线

的渐近线条数为______.
A B C D
A
[解析] 由
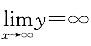
,所以,曲线
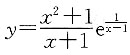
无水平渐近线;
由
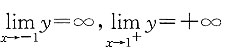
,所以,曲线
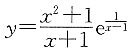
有两条垂直渐近线;
由
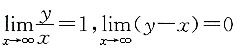
,所以,曲线
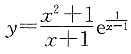
有一条斜渐近线.
求渐近线可遵循“三步走”的方法:先水平,再垂直,最后斜.直接套用极限的公式即可.这是基本题.
5. 双纽线(x
2+y
2)
2=x
2-y
2所围平面图形的面积S=______.
A.

B.
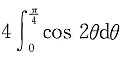
C.
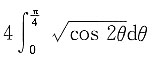
D.
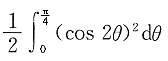
A B C D
A
[解析] 令x=rcos θ,y=rsin θ,代入双纽线公式(x
2+y
2)
2=x
2-y
2中,则可得到r
2=cos 2θ,再根据对称性,有

6. 若
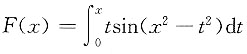
,则F'(x)=______.
- A.xsin x2
- B.-xsin x2
- C.2xsin x2
- D.-2xsin x2
A B C D
A
[解析] 做代换u=x
2-t
2,
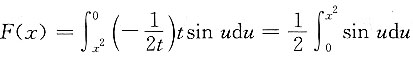
,于是,

对于被积函数中混有自变量的函数求导问题,往往考虑用分离变量法或代换法,将问题化为变上限积分求导问题.
7. 设3维行向量
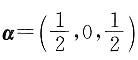
,A=E-α
Tα,B=E+2α
Tα,则AB为______.
A B C D
C
[解析] 这是一道矩阵运算的计算题,直接带入计算即可.
因为,
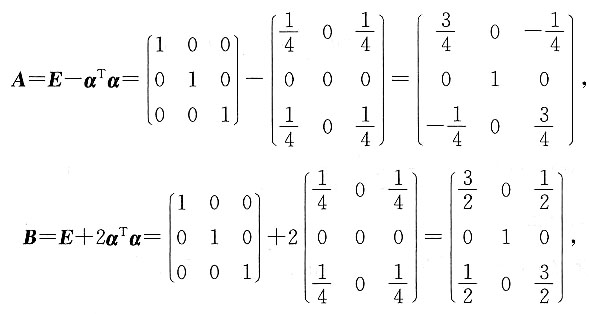
则
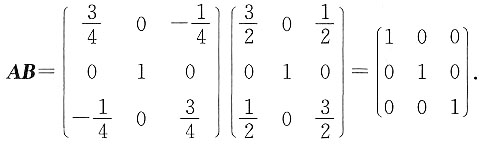
8. 设A是m×n矩阵,r(A)=n,则下列结论不正确的是______.
- A.若AB=O,则B=O
- B.对任意矩阵B,有r(AB)=r(B)
- C.存在B,使得BA=E
- D.对任意矩阵B,有r(BA)=r(B)
A B C D
D
[解析] 因为r(A)=n,所以方程组Ax=0只有零解,而由AB=O,得B的列向量为方程组Ax=0的解,故若AB=O,则B=O;
令Bx=0,ABx=0为两个方程组,显然若Bx=0,则ABx=0,反之,若ABx=0,因为r(A)=n,所以方程组Ax=0只有零解,于是Bx=0,即方程组Bx=0与ABx=0为同解方程组,故r(AB)=r(B);
因为r(A)=n,所以A经过有限初等行变换化为
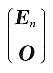
,即存在可逆矩阵P,使得
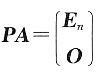
,令B=(E
n O)P,则BA=E;
令
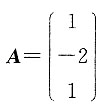
,B=(1,1,1),r(A)=0,但r(BA)=0≠r(B)=1,故选D.
三、数学计算题1. 设P是满足一定条件的常数,且
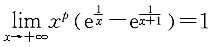
,求P的值.
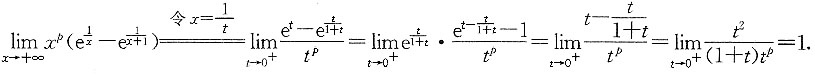
所以,p=2.
2. 设曲线y=f(x)过点(0,0),且当x在x=0处取得增量Δx时,相应的函数值增量Δy=3Δx+o(Δx)(Δx→0),求极限
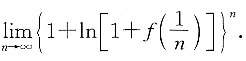
3. 设
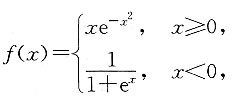
计算
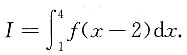
令t=x-2,则
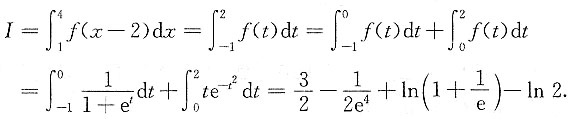
分段函数的积分问题往往利用定积分区间可加性,换元可以大大简化积分的计算.
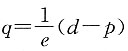 ,其中C为成本,q为需求量(即产量),p为单价,a,b,c,d,e都是正的常数,且d>b,求:
,其中C为成本,q为需求量(即产量),p为单价,a,b,c,d,e都是正的常数,且d>b,求:4. 利润最大时的产量及最大利润;
利润函数L=pq-C=(d-eq)q-(aq
2+bq+c)=(d-b)q-(e+a)q
2-c.
令
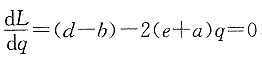
,得
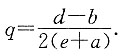
由

,故当
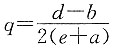
时,利润最大,且
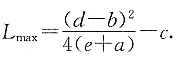
5. 需求对价格的弹性.
由
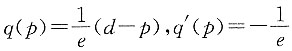
,故需求对价格的弹性为
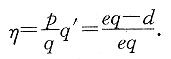
需求乘以价格等于收益,收益减去成本等于利润.对于经济学中的应用问题,我们常根据需求、价格、成本、收益的关系建立函数关系,再利用极值思想处理问题.
6. 设z=f(x,y,)由方程z-y-x+xe
z-y-x=0确定,求dz.
对z-y-x+xe
z-y-x=0两边微分,得
dz-dy-dx+e
z-y-xdx+xe
z-y-x(dz-dy-dx)=0,
即

本题也可以利用两边求偏导的方法,先求出两个偏导数,再求微分.
7. 设随机变量X服从正态分布N(0,4),Y=|X|,求方差D(Y).
依题意,X的概率密度函数
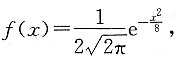
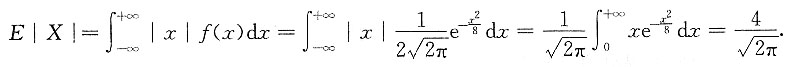
E(X
2)=D(X)+[E(X)]
2=4+0=4,
故
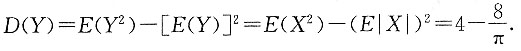
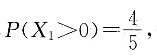
8. 求P(X
2<1);
由题可知,X
1,X
2的分布律为
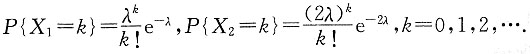
又因为

,得
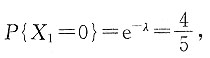
故λ=ln 5.所以
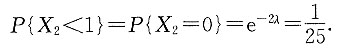
9. 求E[(X
2+1)(X
2-1)].
E[(X2-1)(X2-1)]=E[(X2)2-1]=E(X2)2-1=D(X2)+[E(X2)]2-1
=2λ+(2λ)2-1=4ln25+2ln 5-1.
10. 求向量组α
1=(1,0,2,0)
T,α
2=(0,-1,1,2)
T,α
3=(1,-2,4,4)
T,α
4=(2,-1,4,2)
T的秩和一个极大线性无关组.
依题意,将向量组按列排成矩阵并作初等行变换.
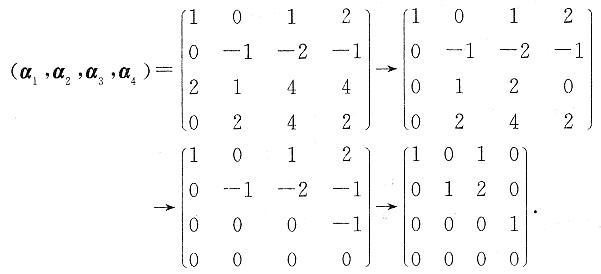
故r(α
1,α
2,α
3,α
4)=3,α
1,α
2,α
4为向量组的一个极大无关组.
11. 已知方程组
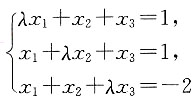
有无穷多个解,求λ的值及方程组的通解.
依题意,对方程组的增广矩阵作初等行变换.
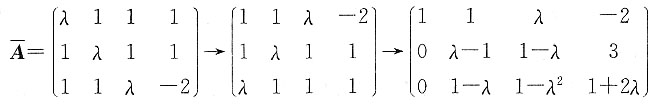
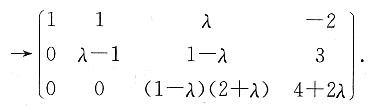
当λ=1时,r(A)=1,
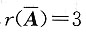
,方程组无解,不符合题意;
当λ=-2时,
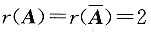
,方程组有无穷多个解,符合题意.
对应的方程组为
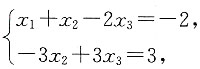
令自由未知量x
3=0,得非齐次方程组的一个特解
η=(-1,-1,0)
T.
对应齐次方程组

的基础解系为
ξ=(1,1,1)
T.
故原方程组的通解为
x=kξ+η=k(1,1,1)
T+(-1,-1,0)
T,k为常数.
四、写作题其中论证有效性分析20分,论说文20分。
1. 论证有效性分析:分析下述论证中存在的缺陷和漏洞,选择若干要点,写一篇600字左右的文章,对该论证的有效性进行分析和评论。(论证有效性分析的一般要点是:概念特别是核心概念的界定和使用是否准确并前后一致,有无各种明显的逻辑错误,论证的论据是否成立并支持结论。结论成立的条件是否充分等。要注意分析的内容深度、逻辑结构和语言表达等)
2014年夏季,“冰桶挑战”风靡全球。活动规则非常简单,被好友点名后必须在24小时内二选一,要么接受“冰桶挑战”,要么向ALS慈善团体捐款。若选择挑战,则需在社交网站上发布自己被冰水浇遍全身的视频,而后任意挑选另外三人发起挑战,以此将活动延续下去。“冰桶挑战”效应显著,所获募捐均创纪录。主要捐款对象“美国ALS协会”在不到1个月的时间内就募集到5330万美元,是去年同期的24倍。但另一方面也开始有人指责其流于游戏化,偏离了活动的初衷。网上出现了一系列的激烈讨论。
正方主要意见:
“冰桶挑战”是一种创新的慈善做法。曾任美国掴客网编辑的尼特赞·齐默尔曼被公认为解读各种流行现象的专家。他说:“将互联网对挑战的热爱同捐款和慈善相结合是一种天才想法。”从某种意义上说,“冰桶挑战”是“开放、平等、协作、分享”的互联网精神在慈善领域的创新应用。
虽然多数人决定把冰水倒到自己头上,而不是捐款到ALS协会。但这些湿淋淋的参与民众仍然看起来像个英雄,因为他们毕竞是为了慈善目的而把自己搞得这么狼狈。从另一方面来说,如果你安安静静地捐钱给ALS协会,而没有在社交媒体上大肆宣传,你的朋友会知道你是好人吗?当然不会,他们只会觉得你自私自利。除了让自己觉得做了件好事,同时也让朋友知道你是个好人,那何乐而不为呢?
反方主要意见:
“冰桶挑战”的目的是提高人们对ALS的认识,同时也号召人们为ALS捐款。现在大佬的做法炒作的意义大于公益,还不如直接做慈善。和外界对活动保持的高昂热情不同,患者小恺表示了对“冰桶挑战”的不看好:“说实话,应该对我们没什么用,大家好像都是在围观名人被浇,而这个活动背后的来龙去脉很少有人知道。”患者小刘表达得则更为直接:“这活动也就这样了,闹腾几天就消停了。”因为不管有多少明星参加活动,接受多少次采访,小刘目前都未从中得到任何实质帮助,而其他几位患者的情况也都和小刘差不多。
最近有一篇文章对“冰桶挑战”的用水量进行了粗略估算:假设挑战者平均用水15升,那么截至目前,大概已浪费1900万升水,该数量相当于9500万瓶装水。这对严重缺水的国家来说,是一种严重的浪费。而实际上,多个国家遭受旱灾的地区均出现了不同程度的反对声音。
[参考范文] 漏洞百出的辩论
原文中正反两方就“冰桶挑战”事件,展开了一场激烈的辩论,但在辩论过程中双方都出现了明显的逻辑缺陷。
首先,正方说“冰桶挑战”是“开放、平等、协作、分享”的互联网精神在慈善领域的创新应用,这一论断有不妥之处。我们承认互联网的精神,但从“冰桶挑战”的规则来看,它却带有一定的强制性,即我挑战你了,而且有人围观了,你看着办吧!这与互联网精神不符。
其次,做慈善,而又让他人知道,这无可厚非,但正方认为“为了慈善目的而把自己搞得很狼狈,却不捐款,仍然像个英雄”,却是欠妥当的。这就像“我不做,我只是告诉你们要做”。这样的人多了,或许对该项目来说会适得其反:这个项目更广为人知,但慈善的目的却未达到。
再次,反方认为“大佬的做法炒作的意义大于公益,还不如直接做慈善”。这一论断也不必然成立。如果通过炒作使更多的人了解此项慈善项目,并且通过以自身为榜样,带动更多的人参与进来,进而实质性地推进该项目的发展,或许其做法也是值得肯定的。
另外,两位患者的看法有不妥之处。项目的实施有一个过程,即使现在未得到有效帮助,不代表后续没有实质性帮助,其间存在时滞性。而且,活动形式本身与活动本身的目的可以是不同的,而活动的目标实现与否与是否了解其根源也没有必然的联系。
最后,该活动用水是全球的数量,1900万吨水对于全球正常用水来说是微不足道的。同时,用瓶装水也有故意夸大之嫌,原数据没有给出其中的饮用水占多大比例。再者,即使这些水不用于此项目,也不一定能运送到缺水地区。
由此可见,原文正方双方在辩论过程中存在较多的不足之处,其辩论的有效性值得商榷。
2. 论说文:根据下述材料,写一篇700字左右的论说文。题目自拟。
中宣部、国家发改委日前发出开展节俭养德全民节约行动的通知,要求以实现中华民族伟大复兴中国梦为根本目标,紧紧围绕社会主义核心价值观的培育践行,深入进行节俭节约宣传教育,广泛开展多种形式的节俭节约实践活动,在全社会营造厉行节约、拒绝浪费的浓厚氛围。
“勤俭节约、勤俭持家”,素来是中华民族的传统美德,但何以需要国家发出如此的通知呢?众所周知,实际中确实有些人做得不尽如人意。办公室没人了,空调、电脑、灯依然在耗费着电,但这些情况在家里却很少发生……
[参考范文] 以教育和制度促进节约
读完材料,我内心被深深地触动了。“勤俭节约、勤俭持家”,素来是中华民族的传统美德,但何以需要国家两大部委发出“开展节俭养德全民节约行动的通知”呢?那是因为“勤俭节约”美德已经缺失得比较严重了。
细究“勤俭节约”缺失的原因,大概有以下两点:一是有些人没有意识到自己的浪费;二是正如材料中所说,有人意识到,但某些地方“节约”,而在另一些地方又不节约了。所以,要想使“勤俭节约”落到实地,恐怕只“宣传教育”是不够的,还得加上制度。以宣传教育和制度管理双重措施来促进节约。
针对没有意识到浪费的人,加强宣传教育是行之有效的。教育的作用之一,是使“未意识到”的人认识到什么是节约,进而促使其改变不节约的行为方式和习惯。比如家庭生活中的空调温度,26度是最佳的人体舒适点,调到20度就是浪费了。个体的浪费虽少,且成本不高,但整个社会的浪费却是巨大的。我想,这些人中至少会有部分人因为“知道节约”而做出改变。
对于已经意识到节约,但不愿做出改变,至少在某些场合不愿做出改变的人,比如在家里“可以节约”,但在单位或其他场合,却是“反正不是我的,浪费不浪费与我无关”的人,则需要用制度来制约。以制度的形式明确什么是节约,违反后有什么样的处理措施,可能对这些人是有效果的,比如单位里的“用电管理制度”等。一方面,制度可以提醒一些人,不能“不节约”;另一方面,可以对“不节约的行为”进行纠正处理,从而达到节约的目的。
从长远来看,节约制度化可以强化宣传教育的效果,从行为实施到养成习惯,在一定程度上可以促进“节约关德”的养成。“遵守交通规则”的美德的养成,也恰能说明这一点。
由此来看,只有一方面加强“培养节约意识的宣传教育”,一方面建立有效的“节约管理制度”,才能促进节约美德的实现。
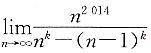 存在且不为零,则常数k=______.
存在且不为零,则常数k=______.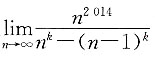 存在且不为零,所以分子、分母为同阶的无穷大量.当k=2 015时,分母的最高次抵消后,最高次也是2 014次,符合题意.
存在且不为零,所以分子、分母为同阶的无穷大量.当k=2 015时,分母的最高次抵消后,最高次也是2 014次,符合题意.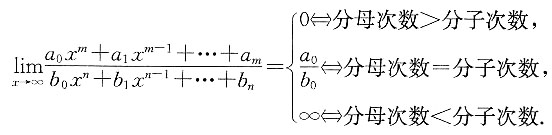
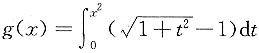 ,若x→0时,f(x)与g(x)是同阶无穷小,则n=______.
,若x→0时,f(x)与g(x)是同阶无穷小,则n=______.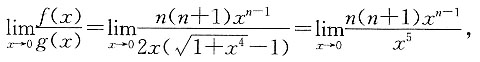
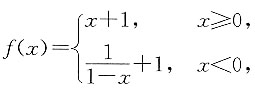 则x=0是f[f(x)]的______.
则x=0是f[f(x)]的______.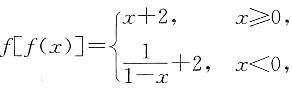 显然,
显然,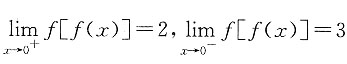 ,故x=0是f[(x)]的跳跃间断点.
,故x=0是f[(x)]的跳跃间断点. 的渐近线条数为______.
的渐近线条数为______.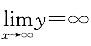 ,所以,曲线
,所以,曲线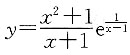 无水平渐近线;
无水平渐近线;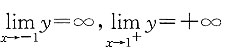 ,所以,曲线
,所以,曲线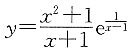 有两条垂直渐近线;
有两条垂直渐近线;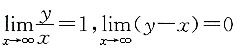 ,所以,曲线
,所以,曲线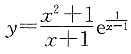 有一条斜渐近线.
有一条斜渐近线.
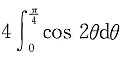
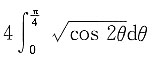
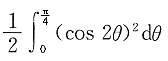

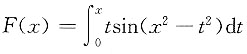 ,则F'(x)=______.
,则F'(x)=______.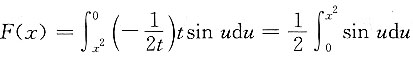 ,于是,
,于是,
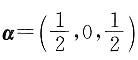 ,A=E-αTα,B=E+2αTα,则AB为______.
,A=E-αTα,B=E+2αTα,则AB为______.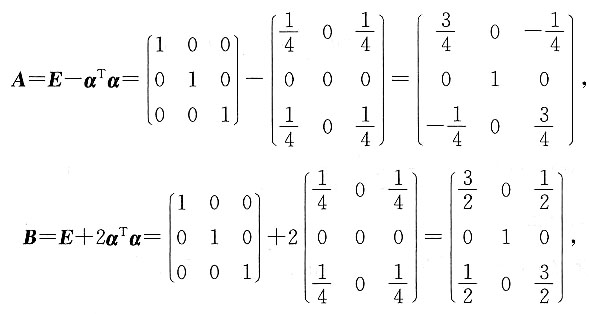
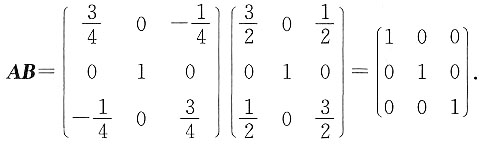
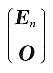 ,即存在可逆矩阵P,使得
,即存在可逆矩阵P,使得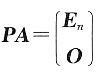 ,令B=(En O)P,则BA=E;
,令B=(En O)P,则BA=E;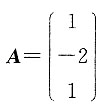 ,B=(1,1,1),r(A)=0,但r(BA)=0≠r(B)=1,故选D.
,B=(1,1,1),r(A)=0,但r(BA)=0≠r(B)=1,故选D.
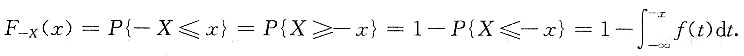
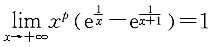 ,求P的值.
,求P的值.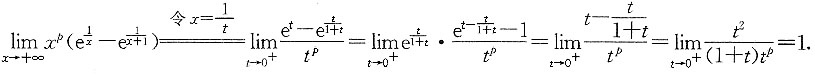
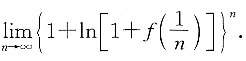
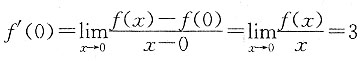 ,所以
,所以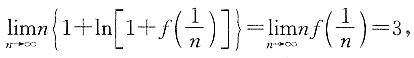
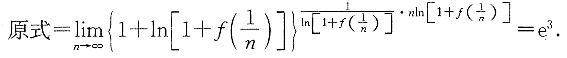
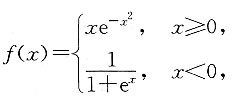 计算
计算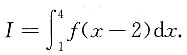
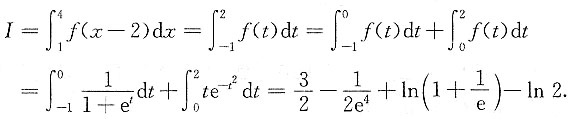
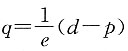 ,其中C为成本,q为需求量(即产量),p为单价,a,b,c,d,e都是正的常数,且d>b,求:
,其中C为成本,q为需求量(即产量),p为单价,a,b,c,d,e都是正的常数,且d>b,求: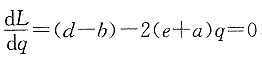 ,得
,得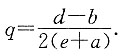
 ,故当
,故当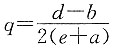 时,利润最大,且
时,利润最大,且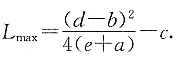
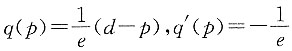 ,故需求对价格的弹性为
,故需求对价格的弹性为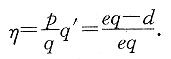

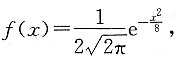
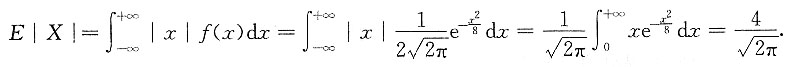
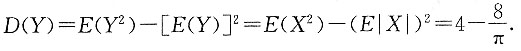
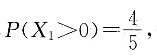
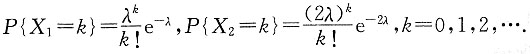
 ,得
,得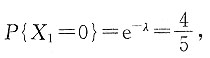
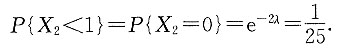

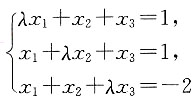 有无穷多个解,求λ的值及方程组的通解.
有无穷多个解,求λ的值及方程组的通解.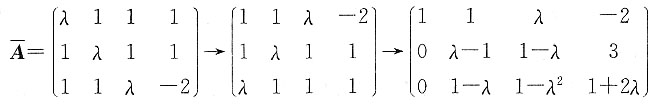
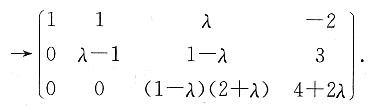
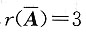 ,方程组无解,不符合题意;
,方程组无解,不符合题意;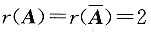 ,方程组有无穷多个解,符合题意.
,方程组有无穷多个解,符合题意.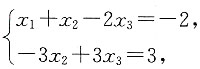 令自由未知量x3=0,得非齐次方程组的一个特解
令自由未知量x3=0,得非齐次方程组的一个特解 的基础解系为
的基础解系为