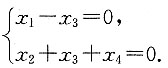一、逻辑推理题下列每题给出的A、B、C、D、E五个选项中,只有一个选项符合试题要求。
六个城市的位置如下表所示: 在这6个城市所覆盖的区域中,有4所医院、2座监狱和2所大学。这8个单位的位置如下:
(1)没有一个单位跨不同的城市。
(2)没有一个城市有两座监狱,也没有一个城市有两所大学。
(3)没有一个城市既有监狱又有大学。
(4)每座监狱位于至少有一所医院的城市。
(5)有大学的两个城市没有共同的边界。
(6)城市3有一所大学,城市6有一座监狱。 二、数学单项选择题下列每题给出的A、B、C、D四个选项中,只有一个选项符合试题要求。
1. 设有两个数列{x
n}与{y
n},以下结论一定正确的是______.
A.若
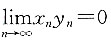
,则必有
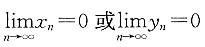
B.若
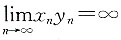
,则必有
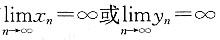
C.若x
ny
n有界,则必有x
ny
n都有界
D.若x
ny
n无界,则必有x
n无界或y
n无界
A B C D
D
[解析] A、B、C项均可通过举反例来说明.
A项错误,可举反例:x
n=1,0,1,0,…;y
n=0,1,0,1,….
B项错误,可举反例:
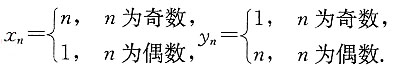
C项错误,可举反例:
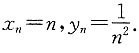
D项正确,可用反证法证明:若x
n,y
n均有界,则x
n,y
n有界,矛盾.
4. 设函数f(x)连续,下列函数中必为偶函数的是______.
A.
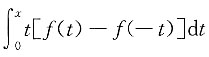
B.
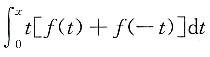
C.
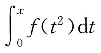
D.
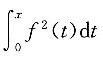
A B C D
B
[解析] 若F(x)为偶函数,必有F(x)=F(-x).令
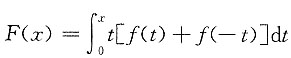
,则

故选B.A项为奇函数,C项也为奇函数,D项不能确定.
5. 下列关于函数
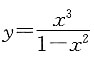
的结论,错误的是______.
- A.有一个零点
- B.有两个极值点
- C.有一个拐点
- D.有两条渐近线
A B C D
D
[解析] 对于
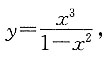
因为
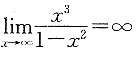
,故函数没有水平渐近线.
因为
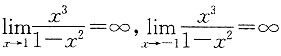
,故函数有铅直渐近线x=1,x=-1.
因为
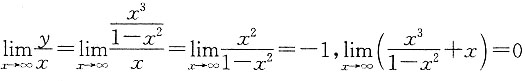
,故函数有斜渐近线y=-x.
综上,曲线有三条渐近线,则D项说法错误.
6. 已知函数z=f(x,y)在点(0,0)某邻域内有定义,且
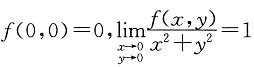
,则f(x,y)在点(0,0)处______.
- A.连续且可微
- B.连续不可微
- C.可微不连续
- D.不连续也不可微
A B C D
A
[解析] 由
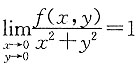
,得
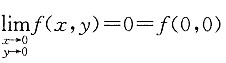
,因此,f(x,y)在点(0,0)处连续.
由
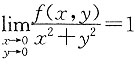
,得
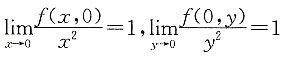
,则f'
x(0,0)=f'
y(0,0)=0
故
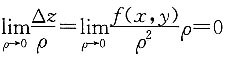
,因此,f(x,y)在点(0,0)处可微,故选A.
7. 设向量组α
1,α
2,α
3线性无关,β
1不能由α
1,α
2,α
3线性表示,而β
2可由α
1,α
2,α
3线性表示,则下列结论正确的是______.
- A.α1,α2,β2线性相关
- B.α1,α2,β2线性无关
- C.α1,α2,α3,β1+β2线性相关
- D.α2,α2,α3,β1+β2线性无关
A B C D
D
[解析] 因为β1不能由α1,α2,α3线性表示,而β2可由α1,α2,α3线性表示,所以β1+β2不能由α1,α2,α3线性表示,从而α1,α2,α3,β1+β2线性无关,故选D.
8. 设A,B,A+B,A
-1+B
-1皆为可逆矩阵,则(A
-1+B
-1)
-1等于______.
- A.A+B
- B.A-1+B-1
- C.A(A+B)-1B
- D.(A+B)-1
A B C D
C
[解析] 按照可逆的定义进行验证.对于C项,有
A(A+B)-1B(A-1+B-1)=[(A+B)A-1]-1(BA-1+E)
=(BA-1+E)-1(BA-1+E)=E.
9. 在3次的独立试验中,每次试验成功的概率为p,且至少成功一次的概率为
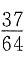
,则概率p=______.
A.
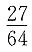
B.
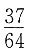
C.
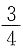
D.
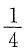
A B C D
D
[解析] 由每次试验成功的概率为p,则3次试验中至少有一次成功的概率为
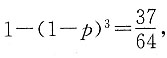
所以
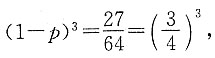
即
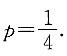
三、数学计算题1. 计算极限
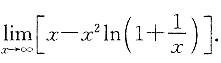
2. 设y=f(x)在x=0处连续,且
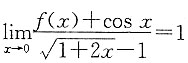
,求曲线y=f(x)在x=0处的切线方程.
因为
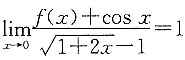
且
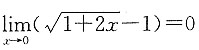
,所以
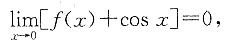
即f(0)+1=0,因此,
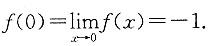
因为当x→0时,
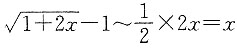
,所以
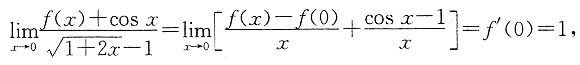
所以f'(0)=1,故所求切线方程为y=x+1.
4. 计算积分
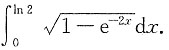
令e
-x=sin t,则
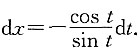
当x=0时,
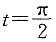
;x=ln 2时,
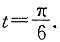
所以,
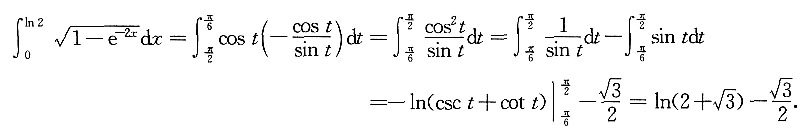
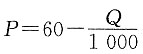 ,其中P是单价,单位:元/件,Q是销量,单位:件,已知产销平衡,求
,其中P是单价,单位:元/件,Q是销量,单位:件,已知产销平衡,求5. 该商品的边际利润;
设利润函数
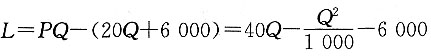
,则边际利润为
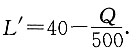
6. 使得利润最大的定价P.
令
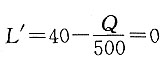
,得Q=20000,则
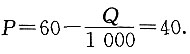
故使得利润最大的定价P为40元/件.
7. 两个盒子中分别装有2个红球,1个白球;2个红球,2个白球.从每个盒中任取一个放在一起,再从中任取一个,求
(1)这个球是红球的概率;
(2)在这个球是红球时,第一个盒中取出的是红球的概率.
A
i={第i个盒中取出的是红球}(i=1,2),B={取出的是红球}.
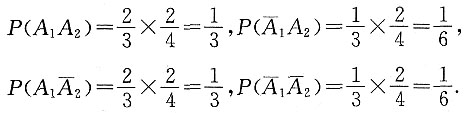
(1)由全概率公式得:
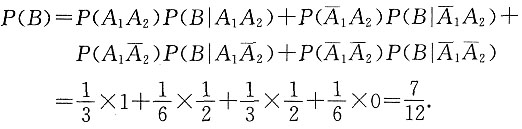
(2)由贝叶斯公式可得:
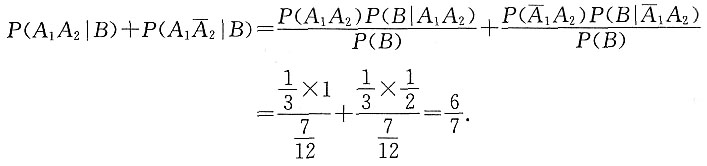
8. 设随机变量X的分布函数为
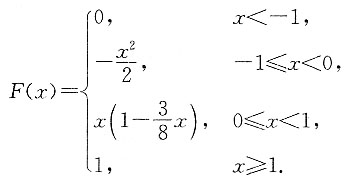
(1)求P{|X|>5X-2};
(2)求E(2|X|-1).
9. 设X=AX+B,其中
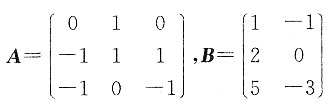
,求X.
依题意,(E-A)X=B,
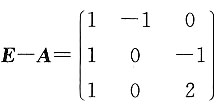
,因为|E-A|=3≠0,所以E-A可逆,故X=(E-A)
-1B.

故
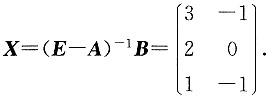
10. 设
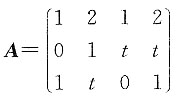
,且方程组AX=0的基础解系中仅含有两个线性无关的解向量,求齐次线性方程组Ax=0的通解.
依题意,r(A)=2,而
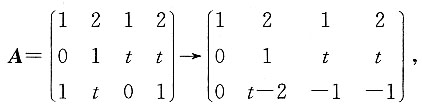
故
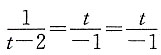
,得t=1,于是

所以由Ax=0得

解得
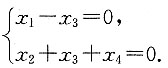
选x
3,x
4为自由未知量,得基础解系
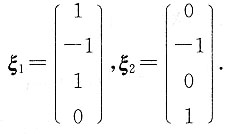
故通解x=k,k
1ξ
1+k
2ξ
2,k
1,k
2为常数.
四、写作题其中论证有效性分析20分,论说文20分。
1. 论证有效性分析:分析下述论证中存在的缺陷和漏洞,选择若干要点,写一篇600字左右的文章,对该论证的有效性进行分析和评论。(论证有效性分析的一般要点是:概念特别是核心概念的界定和使用是否准确并前后一致,有无各种明显的逻辑错误,论证的论据是否成立并支持结论。结论成立的条件是否充分等。要注意分析的内容深度、逻辑结构和语言表达等)
《河南法制报》报道,3月31日至4月1日,张立勇到下辖5个法院调研,在社旗县法院桥头法庭,他提出中午这顿饭非常重要,“法庭庭长必须学会做饭,还要会炒几个菜,今后这项工作要纳入考核机制”。
为何省高院院长强调基层法庭庭长做饭、法官吃好午饭?省高院相关负责人介绍,这和我省基层法庭的现状息息相关。目前,全省法院共有163个基层法院,722个基层人民法庭,承担了全省80%的审判任务。经调查,在基层法庭中连续工作10年以上的有840人,其中连续工作20年以上的有182人。不过.该负责人介绍,由于经费紧张,内部装备配备不到位,基层法庭的法官吃住困难,影响了工作积极性。
张立勇称,“中午饭吃不好,下午工作就不可能干好;中午饭吃不好,大家就不会坚守岗位;如果恰好当事人请客,可能就出去吃人家的了,这事关法院形象,还有腐败之嫌,都是隐患。”
张立勇院长提倡基层法庭要自己解决好吃饭问题,庭长要带头学会做饭。此举目的在于加强基层法院的基础建设,落实中央八项规定和从优待警政策,让法官扎根基层,防止法官接受吃请。如果庭长在法庭做好了午饭,就在一定程度上降低了吃请的可能性。
张立勇的话并非说说而已。南都记者检索发现,南阳市中级人民法院召开专题会议,提出了具体方案。在做饭问题上,南阳法院要求中院班子成员到基层法院调研时,要到每一个法庭吃顿饭,“检验庭长的做饭水平”,同时开展“优秀法庭、优秀法庭庭长”创建评比活动,把“支部建在法庭”,“法庭庭长会做饭”作为评选条件,并在年底对法庭庭长履职情况进行考核,不称职的要采取组织措施。
[参考范文] 经不起推敲的论证
河南高院要求法庭庭长必须学会做饭,并将这项工作纳入考核机制。且不说这一要求是否合适,单其论述过程就存在诸多漏洞。具体分析如下:
首先,基层法庭的法官吃住困难与工作积极性没有必然的因果联系。如果在单位吃住困难,就会影响工作的积极性,那么那些在单位根本就不能吃住的企事业单位员工的积极性是不是就没了呢?但事实却显然不是这样的。可见,这一论据的恰当性值得探讨。
其次,中午饭吃不好,下午工作就不可能干好,就不会坚守岗位。这一断定有些绝对了。吃不好不等于吃不饱,如果能吃饱,但未达到“好”的程度,仅以此为由就做不好工作,甚至不能坚守岗位,那么高院需要考虑的就不仅仅是能不能吃饱饭的问题了。同时,“吃好”的标准是不确定的,也是难以衡量的。
再次,如果吃不好,并恰逢当事人请客,可能就出去吃人家的了。这一断定也似乎难以成立。吃不好,不一定会导致腐败;而腐败也不一定是因为吃得不好。按原文的推理,我们似乎可以得到如下推论:庭长做饭不合胃口,又恰逢当事人请客,也就有理由去吃当事人的了。可见,把吃不好作为腐败的理由是牵强的。
最后,庭长在法庭做好了午饭,也不是必然会降低吃请的可能性。原论断不当地假设了“吃请是因为吃得不好”,同时庭长的做饭水平不明显弱于请客场所的水平,但这实际上是很难成立的。
由此来看,原论证在概念、论据及推理等方面存在诸多漏洞,其有效性是值得怀疑的,河南高院基层法院要求基层法庭庭长必须会做饭的合理性是有待商榷的。
2. 论说文:根据下述材料,写一篇700字左右的论说文,题目自拟。
国务院总理李克强2014年8月22日来到中国铁路总公司考察并主持召开座谈会。他强调,国有企业特别是自然垄断行业要放开竞争性业务,推进公共资源配置市场化,完善法人治理结构,真正成为自主经营、充满活力的市场主体。
自然垄断的合理性并不意味着其有天然的排斥竞争的借口。机场里的商品售价常常高出市区好几倍,石化企业在利润增长五六成的情况下还意图再提高油价,电信企业把获取的超额利润转化为员工的“红包”……很多时候,垄断地位造就了一些企业为所欲为的行为惯性,也激起了社会的不满。
随着改革进入攻坚期和深水区,难啃的“骨头”正变得越来越硬。在一些国有企业当中,长期以来的垄断经营,某种程度上已经异化为利益藩篱。政资政企不分、官商不分的积弊,养成了个别企业这样那样的坏毛病。成本一提就要涨价,经营不力就要政策,在一些环节和领域甚至形成了内部人控制的格局,“挤出效应”日益凸显。
改革要走向深入,这块硬“骨头”躲不开绕不过。只有打破垄断,把那些既不符合经济规律又不符合行业特征的行为清除掉,把市场前景好的项目和竞争性业务拿出来,才能真正激发市场活力,促进国企发展进步,实现国有资产保值增值。
[参考范文] 竞争促发展
李克强总理强调国有企业要放开竞争性业务,引入市场竞争,真正激发市场活力,促进国企发展进步。我深深地赞同,而且真正放开竞争的应该不只是国有企业,而是所有的企业。主动放开竞争,在竞争中才能发展壮大自己。
主动放开竞争,会促使企业不断了解市场的需求,不断提升自身的能力,而这是企业保持不断发展的根本;主动放开竞争,也会促使企业保持警惕,不断超越自己,超越竞争对手,进而保持发展的动力。
总的来看,市场是开放的,竞争者的发展是自由的。竞争者的存在也需要企业树立竞争的意识,放开竞争。谁能更好地满足市场的需求,谁就能得到更好的发展;谁能引领消费者的需求,谁就能获得发展的领先优势。苹果手机创造了3G时代的奇迹,原因之一在于它引领了消费者的需求,而手机巨头诺基亚与摩托罗拉却黯然离场,其原因可能很多,但在新的消费趋势出现时,后者的固守使其忽略了新形势下的竞争,也是重要因素之一。
我们知道,消费者是上帝,而这些上帝的需求是不断变化的、不断前进的。从一定意义上来说,企业与消费者也是竞争关系,即“我需要的是今天的这个,而你提供的是昨天的那个”。这种竞争的来源,在于消费者的自由选择权利和平等交换的理念。如果你的产品与服务不符合市场需求,则消费者可以选择其他竞争者提供的产品与服务。正如我国某些企业,大打民族品牌,甚至爱国旗帜,但其本身做得却不尽如人意,最终还是会失去消费者的支持。企业应树立与消费者竞争的理念,努力超越他们的需求,进而赢得生存与发展。
放开竞争,不等于放弃现有优势。在某些情况下的垄断,可以形成竞争优势,需要保持,但同时要树立竞争意识,而非一味固守。优劣势会在一定条件下相互转化,常将有日思无日,莫待无时思有时。所以,企业应尽早树立竞争意识,放开竞争,不断超越,才能不断发展壮大自己。
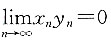 ,则必有
,则必有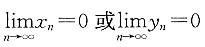
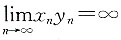 ,则必有
,则必有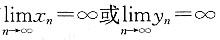
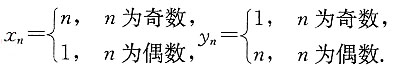
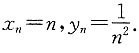
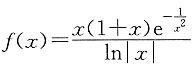 的可去间断点有______个.
的可去间断点有______个.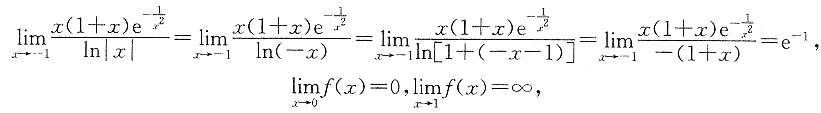
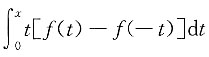
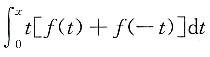
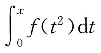
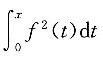
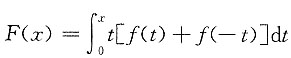 ,则
,则
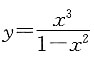 的结论,错误的是______.
的结论,错误的是______.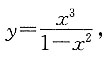
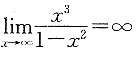 ,故函数没有水平渐近线.
,故函数没有水平渐近线.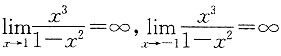 ,故函数有铅直渐近线x=1,x=-1.
,故函数有铅直渐近线x=1,x=-1.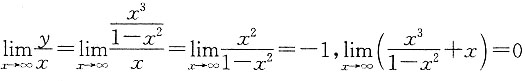 ,故函数有斜渐近线y=-x.
,故函数有斜渐近线y=-x.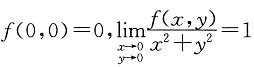 ,则f(x,y)在点(0,0)处______.
,则f(x,y)在点(0,0)处______.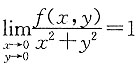 ,得
,得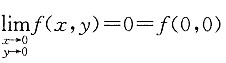 ,因此,f(x,y)在点(0,0)处连续.
,因此,f(x,y)在点(0,0)处连续.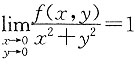 ,得
,得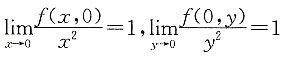 ,则f'x(0,0)=f'y(0,0)=0
,则f'x(0,0)=f'y(0,0)=0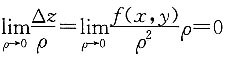 ,因此,f(x,y)在点(0,0)处可微,故选A.
,因此,f(x,y)在点(0,0)处可微,故选A.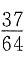 ,则概率p=______.
,则概率p=______.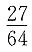
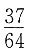
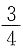
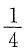
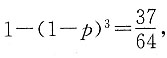
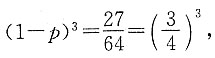
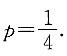
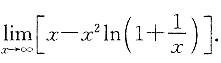
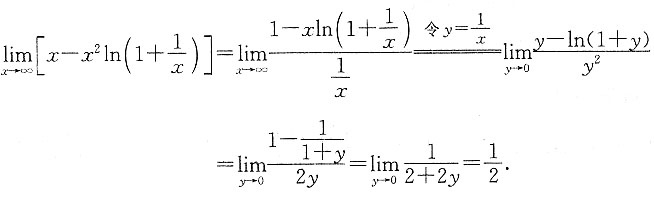
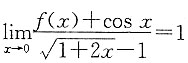 ,求曲线y=f(x)在x=0处的切线方程.
,求曲线y=f(x)在x=0处的切线方程.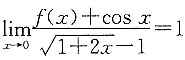 且
且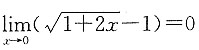 ,所以
,所以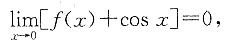
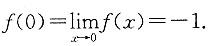
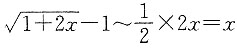 ,所以
,所以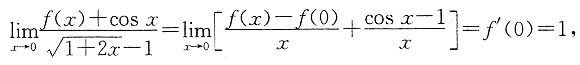
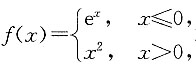 求极限
求极限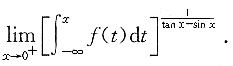
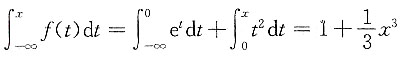 ,则
,则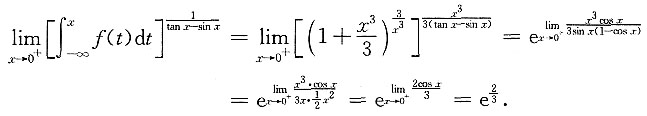
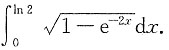
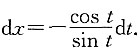 当x=0时,
当x=0时,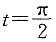 ;x=ln 2时,
;x=ln 2时,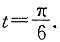 所以,
所以,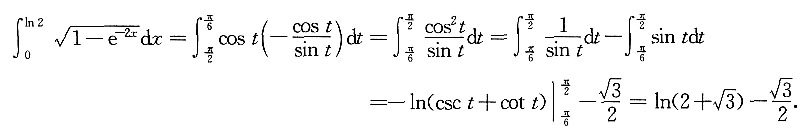
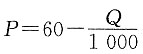 ,其中P是单价,单位:元/件,Q是销量,单位:件,已知产销平衡,求
,其中P是单价,单位:元/件,Q是销量,单位:件,已知产销平衡,求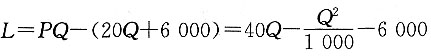 ,则边际利润为
,则边际利润为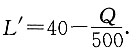
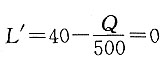 ,得Q=20000,则
,得Q=20000,则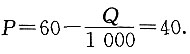 故使得利润最大的定价P为40元/件.
故使得利润最大的定价P为40元/件.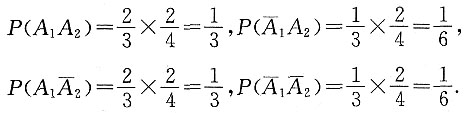
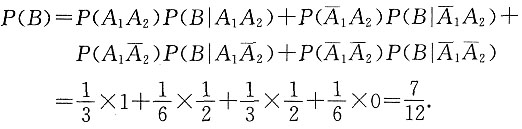

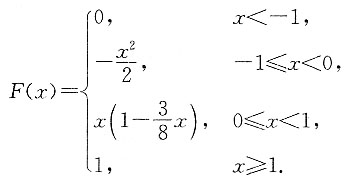
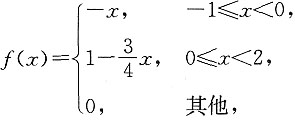 则
则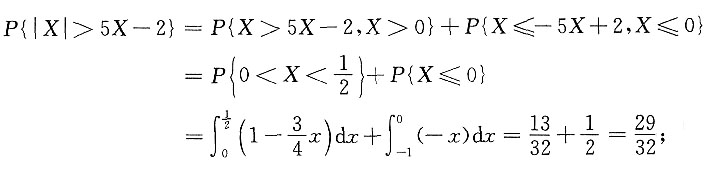
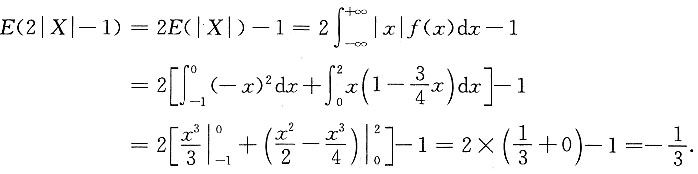
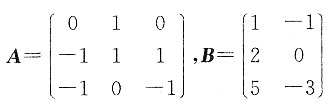 ,求X.
,求X.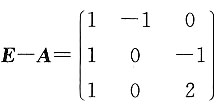 ,因为|E-A|=3≠0,所以E-A可逆,故X=(E-A)-1B.
,因为|E-A|=3≠0,所以E-A可逆,故X=(E-A)-1B.
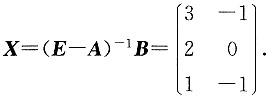
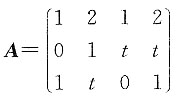 ,且方程组AX=0的基础解系中仅含有两个线性无关的解向量,求齐次线性方程组Ax=0的通解.
,且方程组AX=0的基础解系中仅含有两个线性无关的解向量,求齐次线性方程组Ax=0的通解.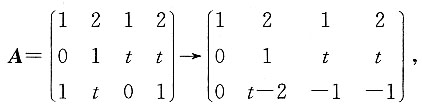
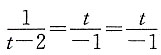 ,得t=1,于是
,得t=1,于是