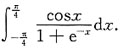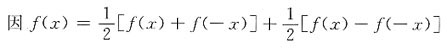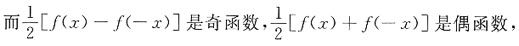一、单项选择题在每小题的四个备选答案中选出一个正确答案.
7. 若曲线y=x
2+1上点M处的切线与直线y=4x+1平行,则点M的坐标为______
- A.(2,5)
- B.(-2,5)
- C.(1,2)
- D.(-1,2)
A B C D
A
[解析] 由题意可知设点M处的坐标为(x
0,y
0),则满足
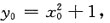
①
又因过点M处的切线平行于直线y=4x+1,则可知斜率相等,
又y'=2x,所以2x
0=4, ②
①与②联立得

解之得x
0=2,y
0=5,
所以点M的坐标为(2,5).
9. 设y
(n-2)=xlnx(n>2,为正整数),则y
(n)=______
A.(x+n)lnx
B.
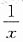
C.
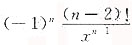
D.0
A B C D
B
[解析] 由题意y
(n-2)=xlnx(n>2,为正整数),
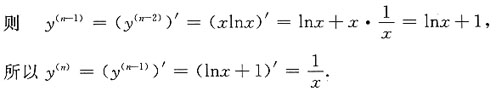
10.
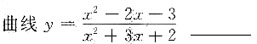
- A.有一条水平渐近线,一条垂直渐近线
- B.有一条水平渐近线,两条垂直渐近线
- C.有两条水平渐近线,一条垂直渐近线
- D.有两条水平渐近线,两条垂直渐近线
A B C D
A
[解析]
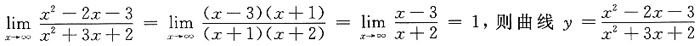
有水平渐近线y=1,又因
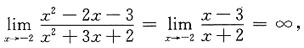
则曲线
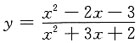
有垂直渐近线x=-2,
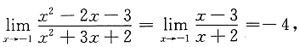
所以我们最终可以得到曲线
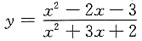
有一条水平渐近线,有一条垂直渐近线.
11. 下列函数在给定区间上满足罗尔定理条件的是______
A.y=|x-1|,[0,2]
B.
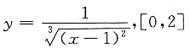
C.y=x
2-3x+2,[1,2]
D.y=xarcsinx,[0,1]
A B C D
C
[解析] 因函数y=x
2-3x+2是由初等函数复合而成.则由一切初等函数在其定义区间内都是连续的.则可知y=x
2-3x+2在闭区间[1,2]上连续,又因y'=2x-3,则函数y=x
2-3x+2在开区间(1,2)内可导,又y(1)=1
2-3×1+2=0 y(2)=2
2-3×2+2=0,所以y(1)=y(2),则存在ξ∈(1,2)使f'(ξ)=0,即2ξ-3=0,
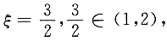
故选C.
所以函数y=x
2-3x+2在闭区间[1,2]上满足罗尔定理的条件.
14. 设f(x)为可导函数,且f'(2x-1)=e
x,则f(x)=______
A.
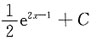
B.
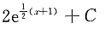
C.
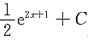
D.
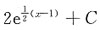
A B C D
B
[解析] 由题意可知:设2x-1=t,则

所以
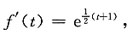
则积分得
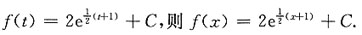
15. 导数
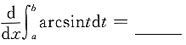
A.arcsinx
B.0
C.arcsinb-arcsina
D.
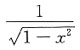
A B C D
B
[解析] 由题意可知
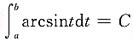
(C为常数).则
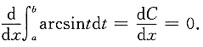
16. 下列广义积分收敛的是______
A.
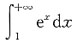
B.
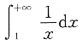
C.

D.
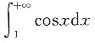
A B C D
C
[解析] 对于A选项:
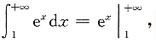
发散;对于B选项:
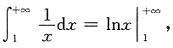
发散;对于C选项:
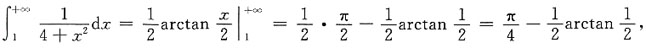
收敛;对于D选项:
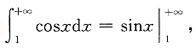
发散;综上所述,选项C正确.
20. 设方程e
2z-xyz=0确定了函数z=f(x,y),则
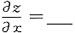
A.
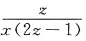
B.
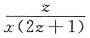
C.
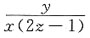
D.
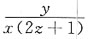
A B C D
A
[解析] 由题意可知 e
2z-xyz=0,令F(x,y,z)=e
2z-xyz,则F
x=-yz,F
z=2e
2z-xy,
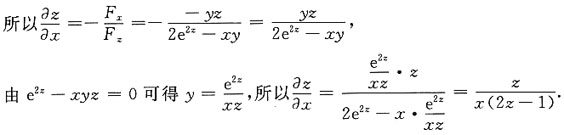
22. 二元函数z=2xy-3x
2-3y
2+20在定义域内______
- A.有极大值,无极小值
- B.无极大值,有极小值
- C.有极大值,有极小值
- D.无极大值,无极小值
A B C D
A
[解析] 由二元函数z=2xy-3x
2-3y
2+20,
则z
x=2y-6x,z
y=2x-6y
令z
x=0,z
y=0,
则联立方程组得
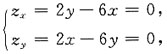
求得驻点为(0,0),
再求出二阶偏导数z
xx=-6,z
xy=2,z
yy=-6,
在点(0,0)处AC-B
2=(-6)×(-6)-2
2=32>0,又A<0,
所以二元函数z=2xy-3x
2-3y
2+20在点(0,0)处取得极大值.且函数z=2xy-3x
2-3y
2+20无极小值.
23. 设D为圆周x
2+y
2-2x-2y+1=0围成的闭区域,则
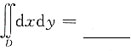
A B C D
A
[解析] D为圆周x
2+y
2-2x-2y+1=0围成的闭区域,即以点(1,1)为圆心,半径为1的圆域,由二重积分的性质可知
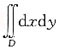
等于区域D的面积,即

24. 交换二次积分
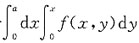
(a>0,常数)的积分次序后可化为______
A.
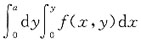
B.
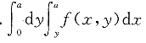
C.
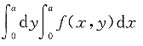
D.
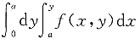
A B C D
B
[解析] 由题意可知,积分区域D可表示为
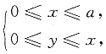
如图所示
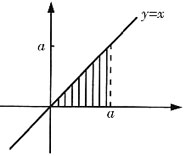
转化为先对x后对y的积分区域D又可表示为
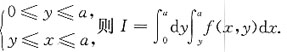
25. 若二重积分
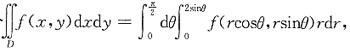
则积分区域D为______
A.x
2+y
2≤2x
B.x
2+y
2≤2
C.x
2+y
2≤2y
D.
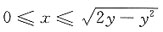
A B C D
D
[解析] 由题意可知,积分区域D可表示为
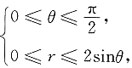
如图所示
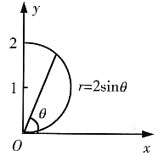
则转化为直角坐标系下的积分区域D为(y-1)
2+x
2=1(x≥0)
即区域D可表示为
28. 设幂级数
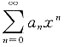
(a
n为常数,n=0,1,2…)在点x=-2处收敛,则级数
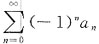
______
A B C D
A
[解析] 令u
n=(-1)
na
n,v
n=a
nx
n,又因为幂级数

(a
n为常数,n=0,1,2…)在点x=-2处收敛,所以
|u
n|=|(-1)
na
n|=|a
n|≤|a
n(-2)
n|=2
n|a
n|,
则
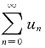
绝对收敛,即
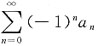
绝对收敛,也可以由阿贝尔定理直接得到.
29. 微分方程sinxcosydy+cosxsinydx=0的通解为______
- A.sinxcosy=C
- B.cosxsiny=C
- C.sinxsiny=C
- D.cosxcosy=C
A B C D
C
[解析] 由微分方程sinxcosydy+cosxsinydx=0.
则
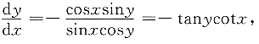
则-cotydy=cotxdx,所以-ln|siny|+C
1=ln|sinx|,
即ln|sinxsiny|=C
1,|sinxsiny|=e
C1,
故sinxsiny=C,(C为任意常数).
二、填空题1. 设函数
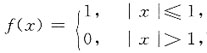
则f(sinx)=______.
1
[解析] 因为函数
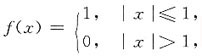
而|sinx|≤1,则f(sinx)=1.
2.
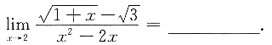
[解析]
3. 设函数y=arctan2x,则dy=______.
[解析] 由函数y=arctan2x,则
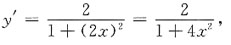
则
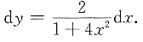
4. 设函数f(x)=x
3+ax
2+bx在x=-1处取得极小值-2,则常数a和b分别为______.
a=4,b=5
[解析] 函数f(x)=x
3+ax
2+bx在其定义域内连续,且处处可导.又f'(x)=3x
2+2ax+b.令f'(x)=0.得驻点
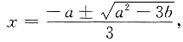
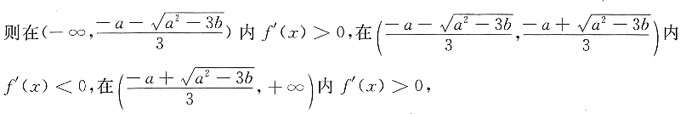
故函数f(x)=x
3+ax
2+bx在
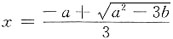
处取极小值,
即
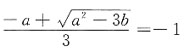
①,f(-1)=-2=-1+x-b ②,
①与②联立得
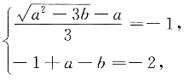
解之得a=4,b=5.
5. 曲线y=x
3-3x
2+2x-1的拐点为______.
(1,-1)
[解析] 由函数y=x3-3x2+2x-1可得y'=3x2-6x+2,y"=6x-6.令y"=0,即6x-6=0,则x=1.当x>1时,y">0,当x<1时,y"<0;因此当x=1时,y=-1,所以可得(1,-1)为函数y=x3-3x2+2x-1的拐点.
6. 设函数f(x)、g(x)均可微,且同为某函数的原函数,f(1)=3,g(1)=1,则f(x)-g(x)=______.
2
[解析] 由函数f(x),g(x)均可微,且同为某函数的原函数,因此可设某函数为φ(x),则∫φ(x)dx=f(x)+C1,∫φ(x)dx=g(x)+C2,
则f(x)-g(x)=∫φ(x)dx-C1-(∫φ(x)dx-C2)=C2-C1=C,
即f(x)与g(x)相差一个固定的常数,又因f(1)=3,g(1)=1,
则f(x)-g(x)=f(1)-g(1)=3-1=2.
7.
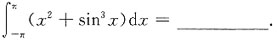
[解析] 由对称区间上函数积分的性质可知,
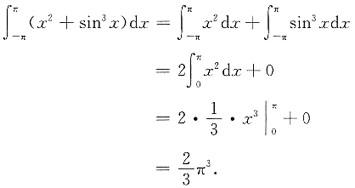
9. 向量a={1,1,2}与向量b={2,-1,1}的夹角为______.
[解析] 由题意可知a={1,1,2},b={2,-1,1},
则a·b=1×2+1×(-1)+2×1=3.
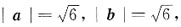
所以
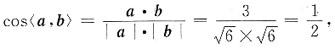
则
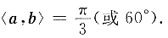
10. 曲线
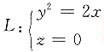
绕x轴旋转一周所形成的旋转曲面方程为______.
y2+z2=2x
[解析] 设M
1(x
1,y
1,0)为曲线L上任意一点,那么有
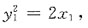
当曲线l绕x轴旋转时,点M
1绕x轴旋转到另一点M(x,y,z),这时x=x
1保持不变,且点M到x轴的距离
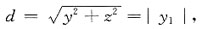
将x=x
1,
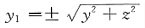
代入得y
2+z
2=2x.
11. 设函数
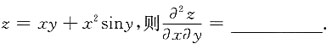
1+2xcosy
[解析] 由函数z=xy+x
2siny,则
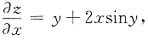
所以
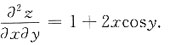
12. 设区域D={(x,y)|0≤x≤1,-1≤y≤1},则
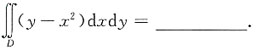
[解析] 由积分区域D={(x,y)|0≤x≤1,-1≤y≤1},
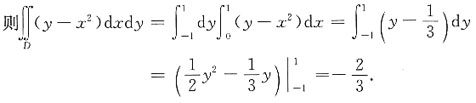
13. 函数f(x)=e
-x2在x=0处展开的幂级数是______.
[解析] 由函数f(x)=e
x在x=0处展开的幂级数为
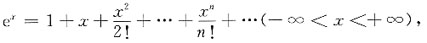
把e
x的幂级数展开式中的x换成-x
2,就可得到函数f(x)=e
-x2的幂级数展开式
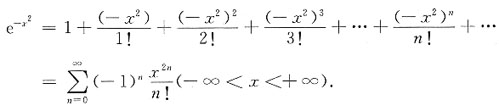
14. 幂级数
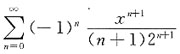
的和函数为______.
[解析] 先求收敛域,
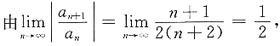
则收敛半径为R=2,在端点x=2处,幂级数为
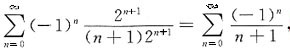
是收敛的交错级数,在端点x=-2处,幂级数为
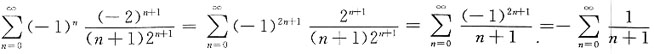
是发散的.因此收敛域为I=(-2,2]
设和函数为s(x),即
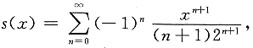
利用和函数的性质可得到
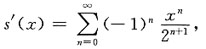
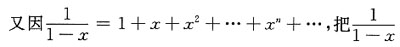
的幂级数展开式中的x换成
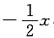
,
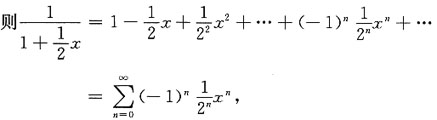
所以
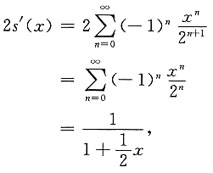
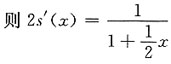
对上式从0到x积分,得
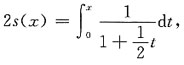
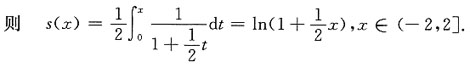
15. 通解为y=C
1e
-x+C
2e
3x(C
1、C
2为任意常数)的二阶线性常系数齐次微分方程为______.
y"-2y'-3y=0
[解析] 由通解为y=C1e-x+C2e3x(C1,C2为任意常数)可知λ1=-1,λ2=3.
则可知微分方程的特征方程为
r2-2r-3=0.
则通解为y=C1e-x+C2e3x(C1,C2为任意常数)的二阶线性常系数齐次微分方程为
y"-2y'-3y=0
三、计算题(每小题5分,共40分)
2. 求函数y=(x
2+3x)
sin2x的导数
[解析] 方法一 将函数y=(x
2+3x)
sin2x两边取自然对数,有
lny=sin2x·ln(x
2+3x),两边对x求导,得:
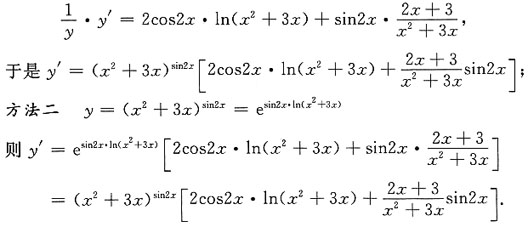
3. 求不定积分
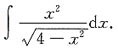
[解析]
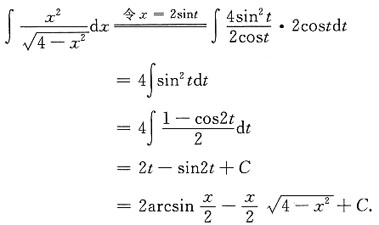
4. 计算定积分
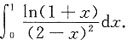
[解析]
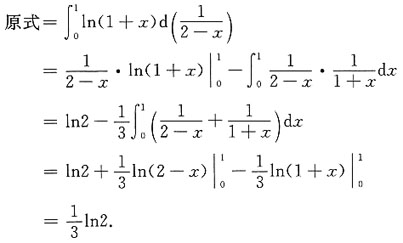
5. 设z=f(2x+y)+g(x,xy),其中f(t),g(u,v)皆可微,求
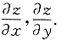
[解析]
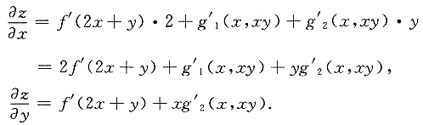
6. 计算二重积分
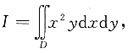
其中区域D由y=x,y=2x及x=1所围成.
[解析] 积分区域D可表示为
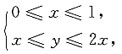
7. 求幂级数
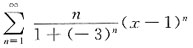
的收敛区间(不考虑区间端点的情况)
[解析] 方法一
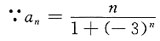
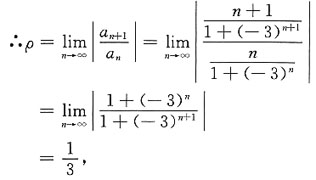
∴收敛半径
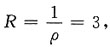
∴收敛区间为:|x-1|<3,即(-2,4);
方法二
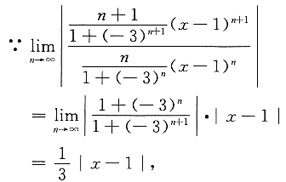
∴由比值判别法知,当
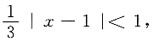
即|x-1|<3时,幂级数收敛,而当
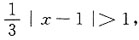
即|x-1|>3时,幂级数发散.
∴所求收敛区间为:|x-1|<3,即(-2,4).
8. 求微分方程x
2dy+(2xy-x+1)dx=0的通解.
[解析] 方法一 方程可化为x
2dy+2xydx=(x-1)dx,
即d(x
2y)=(x-1)dx,
两边积分有
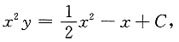
故所求通解为:
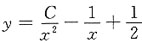
,C为任意常数;
方法二 方程可化为
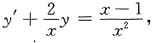
于是,
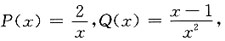
所以,方程的通解为:
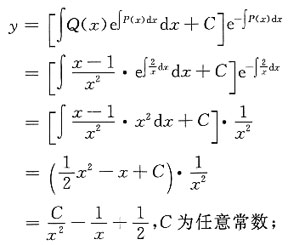
方法三 方程可化为
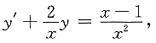
该方程对应的齐次方程的通解为:
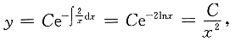
令原方程的通解为:
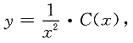
将其代入原微分方程,有
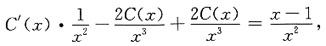
于是,C'(x)=x-1,
所以,
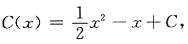
故原方程的通解为:
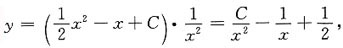
C为任意常数.
四、应用题(每小题7分,共14分)
1. 某公司的甲、乙两厂生产同一种产品,月产量分别是x、y(千件),甲厂的月生产成本是C
1=x
2-2x+5(千元),乙厂的月生产成本是C
2=y
2+2y+3(千元).若要求该产品每月总产量为8千件,并使总成本最小,求甲、乙两工厂的最优产量和相应的最小成本.
[解析] 本题为求函数z=f(x,y)=x
2+y
2-2x+2y+8在条件x+y-8=0下的条件极值.
方法一 用拉格朗日乘数法
总成本f(x,y)=x
2+y
2-2x+2y+8,
约束条件φ(x,y)=x+y-8=0,
作辅助函数F(x,y)=x
2+y
2-2x+2y+8+λ(x+y-8),
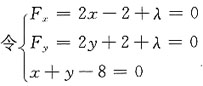
解得x=5,y=3,
由于驻点(5,3)唯一,实际中确有最小值,所以当x=5千件,y=3千件时使总成本最小.最小成本为f(5,3)=38千元;
方法二 化条件极值为无条件极值
总成本为z=f(x,y)=x
2+y
2-2x+2y+8,
约束条件x+y-8=0,
将y=8-x代入f(x,y)中,得
z=x
2+(8-x)
2-x+2(8-x)+8=2x
2-20x+88,
z
x=4x-20,令z
x=0,得x=5,
因为z
xx=4>0,所以x=5时z取极小值.又因为极值点唯一,所以x=5时z取最小值.此时y=3,故x=5千件,y=3千件时,总成本最小.
最小成本为f(5,3)=38千元.
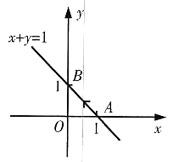
2. 由曲线y=(x-1)(x-2)和x轴围成一平面图形,求此平面图形绕y轴旋转一周所成的旋转体的体积.
[解析] 方法一 曲线y=(x-1)(x-2)和x轴围的平面图形如图,
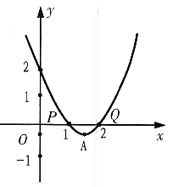
因抛物线顶点A的坐标为
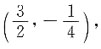
且由y=(x-1)(x-2)可求得曲线段
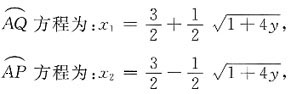
于是,所求旋转体的体积为:

方法二(柱壳法) 选x为积分变量,得旋转体体积:
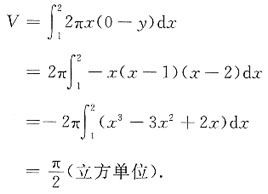
五、证明题(6分)
1. 设f(x)在[-a,a]上连续(a>0,为常数),证明:
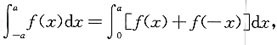
并计算:
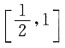
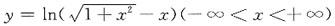 是______
是______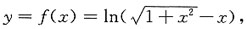 则由题意可知函数y=f(x)的定义域为(-∞,+∞),又因
则由题意可知函数y=f(x)的定义域为(-∞,+∞),又因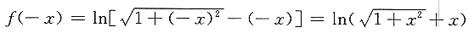
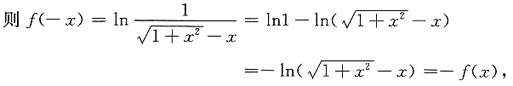
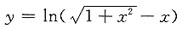 是奇函数.
是奇函数.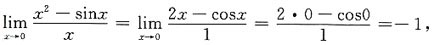
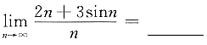
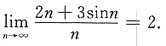
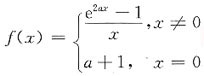 在x=0处连续,则常数a=______
在x=0处连续,则常数a=______ 在x=0处连续,
在x=0处连续,
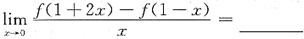
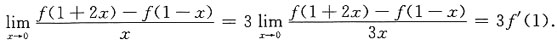
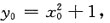 ①
① 解之得x0=2,y0=5,
解之得x0=2,y0=5,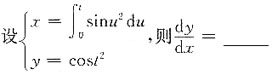
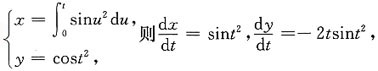
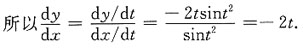
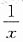
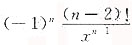
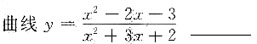
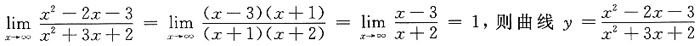 有水平渐近线y=1,又因
有水平渐近线y=1,又因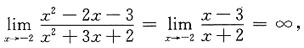 则曲线
则曲线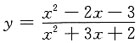 有垂直渐近线x=-2,
有垂直渐近线x=-2,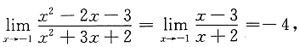 所以我们最终可以得到曲线
所以我们最终可以得到曲线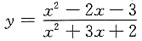 有一条水平渐近线,有一条垂直渐近线.
有一条水平渐近线,有一条垂直渐近线.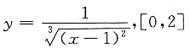
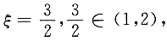 故选C.
故选C.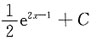
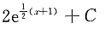
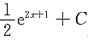
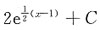
 所以
所以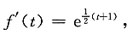 则积分得
则积分得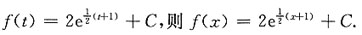
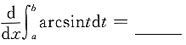
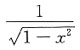
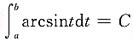 (C为常数).则
(C为常数).则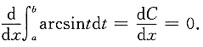
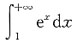
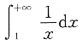

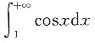
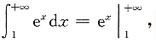 发散;对于B选项:
发散;对于B选项: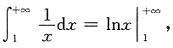 发散;对于C选项:
发散;对于C选项: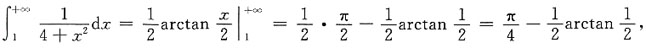 收敛;对于D选项:
收敛;对于D选项: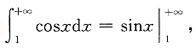 发散;综上所述,选项C正确.
发散;综上所述,选项C正确.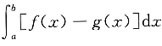
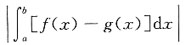
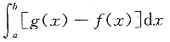
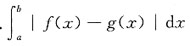
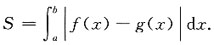
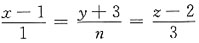 与平面3x-4y+3z+1=0平行,则常数n=______
与平面3x-4y+3z+1=0平行,则常数n=______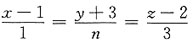 则可得直线的方向向量s={1,n,3},由平面方程3x-4y+3z+1=0,则可得到平面的法线向量,n={3,-4,3},又因直线
则可得直线的方向向量s={1,n,3},由平面方程3x-4y+3z+1=0,则可得到平面的法线向量,n={3,-4,3},又因直线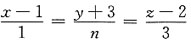 与平面3x-4y+3z+1=0平行,则可知s·n=0,即3×1+(-4)×n+3×3=0,解之得n=3.
与平面3x-4y+3z+1=0平行,则可知s·n=0,即3×1+(-4)×n+3×3=0,解之得n=3.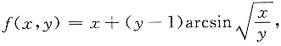 则偏导数fx(x,1)为______
则偏导数fx(x,1)为______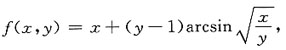
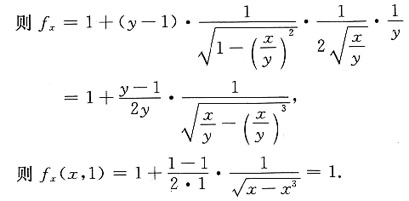
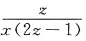
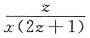
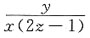
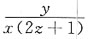
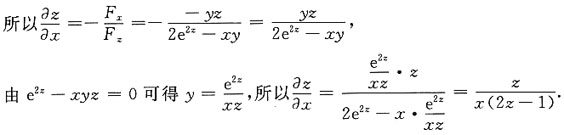
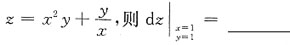
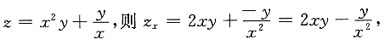
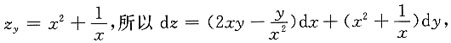
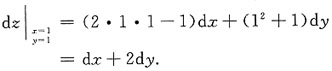
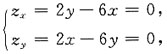
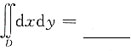
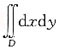 等于区域D的面积,即
等于区域D的面积,即
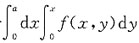 (a>0,常数)的积分次序后可化为______
(a>0,常数)的积分次序后可化为______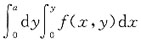
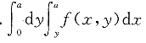
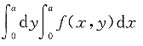
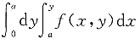
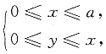 如图所示
如图所示
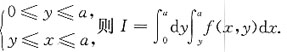
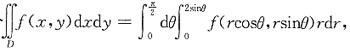 则积分区域D为______
则积分区域D为______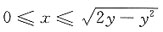
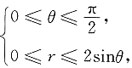 如图所示
如图所示
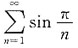
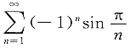
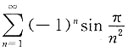
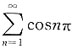

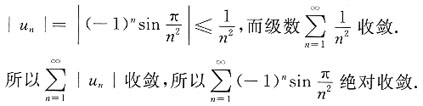
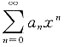 (an为常数,n=0,1,2…)在点x=-2处收敛,则级数
(an为常数,n=0,1,2…)在点x=-2处收敛,则级数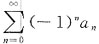 ______
______ (an为常数,n=0,1,2…)在点x=-2处收敛,所以
(an为常数,n=0,1,2…)在点x=-2处收敛,所以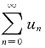 绝对收敛,即
绝对收敛,即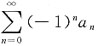 绝对收敛,也可以由阿贝尔定理直接得到.
绝对收敛,也可以由阿贝尔定理直接得到.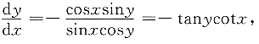
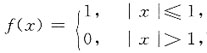 则f(sinx)=______.
则f(sinx)=______.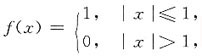 而|sinx|≤1,则f(sinx)=1.
而|sinx|≤1,则f(sinx)=1.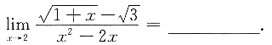
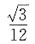
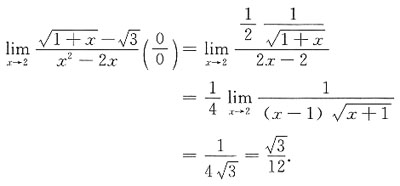
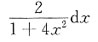
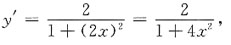
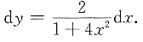
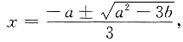
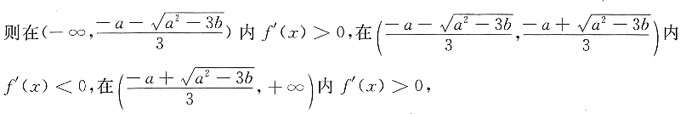 故函数f(x)=x3+ax2+bx在
故函数f(x)=x3+ax2+bx在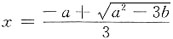 处取极小值,
处取极小值,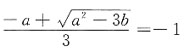 ①,f(-1)=-2=-1+x-b ②,
①,f(-1)=-2=-1+x-b ②,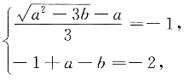 解之得a=4,b=5.
解之得a=4,b=5.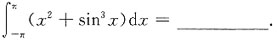
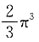
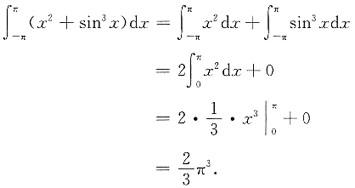
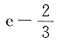
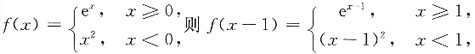
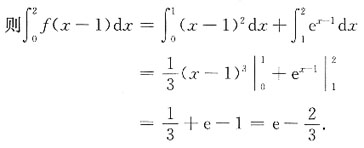
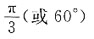
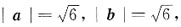 所以
所以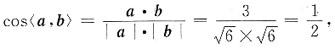
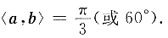
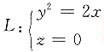 绕x轴旋转一周所形成的旋转曲面方程为______.
绕x轴旋转一周所形成的旋转曲面方程为______.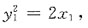 当曲线l绕x轴旋转时,点M1绕x轴旋转到另一点M(x,y,z),这时x=x1保持不变,且点M到x轴的距离
当曲线l绕x轴旋转时,点M1绕x轴旋转到另一点M(x,y,z),这时x=x1保持不变,且点M到x轴的距离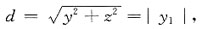 将x=x1,
将x=x1,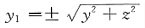 代入得y2+z2=2x.
代入得y2+z2=2x.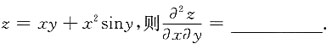
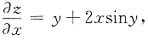 所以
所以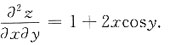
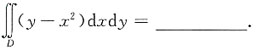
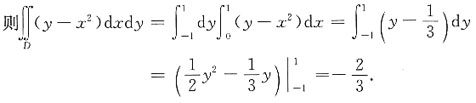
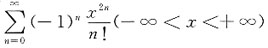
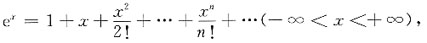
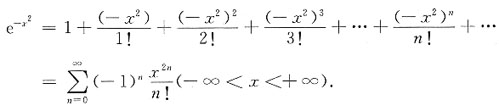
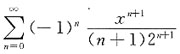 的和函数为______.
的和函数为______.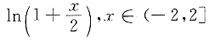
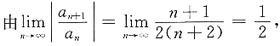 则收敛半径为R=2,在端点x=2处,幂级数为
则收敛半径为R=2,在端点x=2处,幂级数为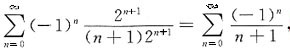 是收敛的交错级数,在端点x=-2处,幂级数为
是收敛的交错级数,在端点x=-2处,幂级数为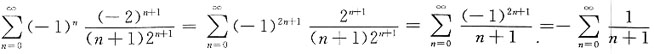
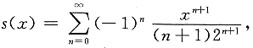
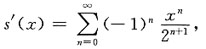
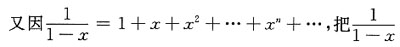 的幂级数展开式中的x换成
的幂级数展开式中的x换成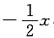 ,
,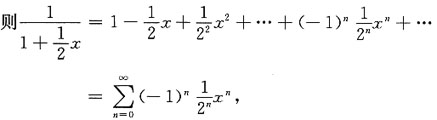
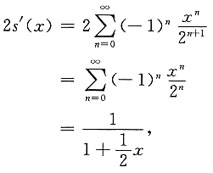
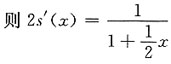 对上式从0到x积分,得
对上式从0到x积分,得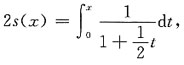
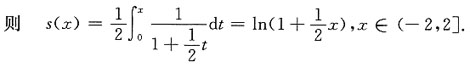
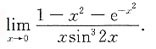


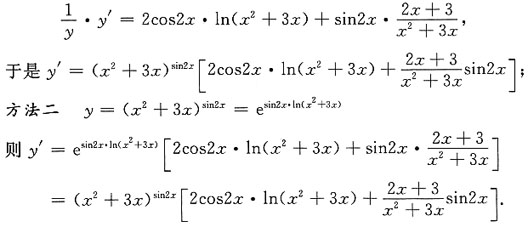
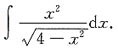
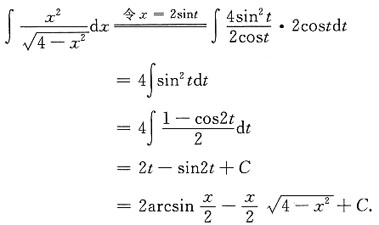
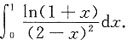
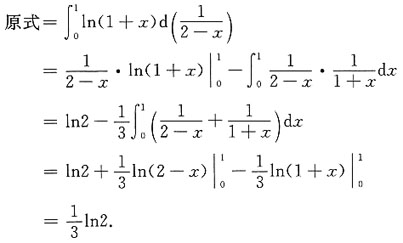
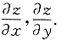
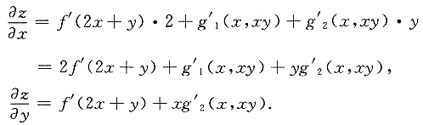
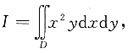 其中区域D由y=x,y=2x及x=1所围成.
其中区域D由y=x,y=2x及x=1所围成.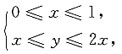
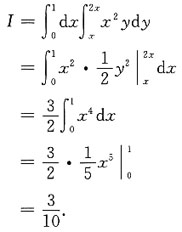
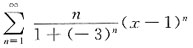 的收敛区间(不考虑区间端点的情况)
的收敛区间(不考虑区间端点的情况)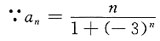
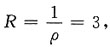
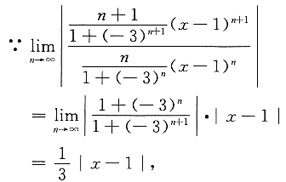
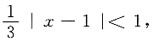 即|x-1|<3时,幂级数收敛,而当
即|x-1|<3时,幂级数收敛,而当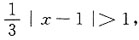 即|x-1|>3时,幂级数发散.
即|x-1|>3时,幂级数发散.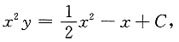
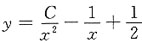 ,C为任意常数;
,C为任意常数;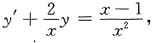
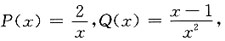
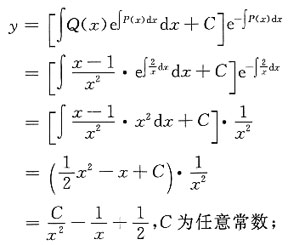
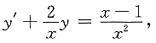
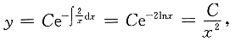
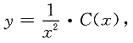
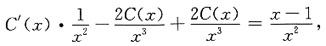
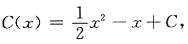
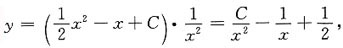 C为任意常数.
C为任意常数.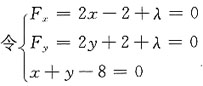

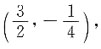 且由y=(x-1)(x-2)可求得曲线段
且由y=(x-1)(x-2)可求得曲线段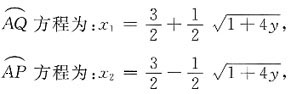

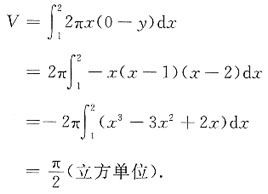
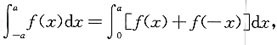 并计算:
并计算: