一、单项选择题(在每个小题的四个备选答案中选出一个正确的答案)
2. 极限
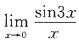
等于______
A.0
B.1
C.
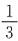
D.3
A B C D
D
[解析]
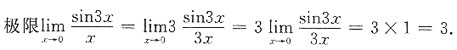
5. 曲线y=x
2与直线y=1所围成的图形的面积为______
A.
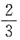
B.
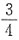
C.
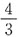
D.1
A B C D
C
[解析] 方法一
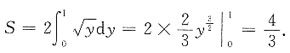
方法二
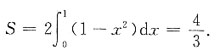
6. 定积分
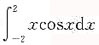
等于______
A.-1
B.0
C.1
D.
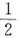
A B C D
B
[解析] 方法一 ∵y=x·cosx为奇函数,
∴在对称区间[-2,2]上函数积分为0.
方法二
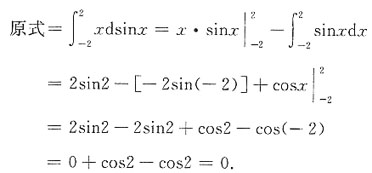
8. 曲线y=x
2在点(1,1)处的法线方程为______
A.y=x
B.
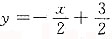
C.
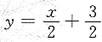
D.
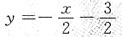
A B C D
B
[解析]

故所求法线方程为
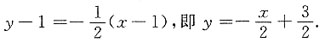
9. 设f(x)在x
0处不连续,则______
A.f'(x
0)存在
B.f'(x
0)不存在
C.
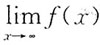
必存在
D.f(x)在x
0处可微
A B C D
B
[解析] 不连续
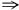
不可导.
10.
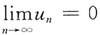
是级数
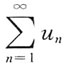
收敛的______条件.
A B C D
A
[解析] 当级数
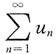
收敛时,
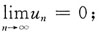
而当
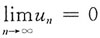
时,级数
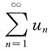
不一定收敛.
二、填空题1. 若
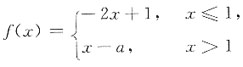
在x=1处连续,则a=______.
2
[解析]
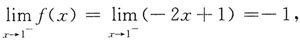
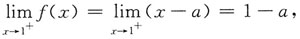
∵f(x)在x=1处连续,∴1-a=-1,∴a=2.
2. x=0是函数
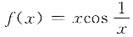
的第______类间断点.
一
[解析]
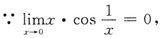
∴x=0是第一类间断点.
3. 若曲线y=f(x)在点(x
0,f(x
0))处的切线平行于直线y=2x-3,则f'(x
0)=______.
4. 函数f(x)=2x
3-9x
2+12x的单调减区间是______.
(1,2)
[解析] f'(x)=6x2-18x+12=6(x2-3x+2)=6(x-1)(x-2),
令f'(x)<0,则有1<x<2,
所以f(x)的单调减区间为(1,2).
5. 设y=cos(sinx),则dy=______.
-sin(sinx)·cosxdx
[解析] y'=-sin(sinx)·(sinx)'=-sin(sinx)·cosx,
所以,dy=-sin(sinx)·cosxdx.
6. ∫df(x)=______.
f(x)+C
[解析] ∵d[f(x)]=f'(x)dx,
∴∫d[f(x)]=∫f'(x)dx=f(x)+C.
7.
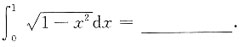
[解析] 令x=sinu,则
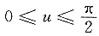
,dx=cosudu,

8. “函数z=f(x,y)在点(x,y)处的偏导数
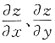
存在”是“函数z=f(x,y)在点(x,y)处可微分”的______条件.
必要
[解析] 若二元函数在某点处可微,则此函数在该点的两个偏导数都存在,反之不成立.
9. 微分方程y"-4y'-5y=0的通解为______.
y=C1e5x+C2e-x(C1,C2为任意常数)
[解析] 特征方程为λ2-4λ-5=0,(λ-5)(λ+1)=0,特征根为λ1=5,λ2=-1.所以该方程的通解为y=C1e5x+C2e-x,C1,C2为任意常数.
10. 幂级数

的收敛区间为______.
(-∞,+∞)
[解析]
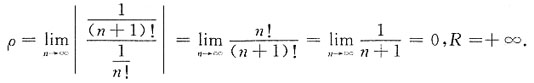
所以,收敛区间为(-∞,+∞).
三、计算题(每小题5分,共50分)
1.
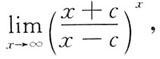
(其中c为常数).
[解析]
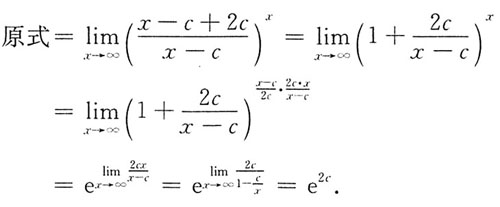
2.
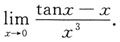
[解析]
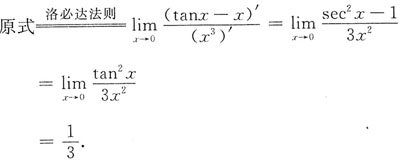
3. 设函数y=y(x)由方程2
xy=x+y所确定,求
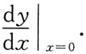
[解析] ∵(2
xy)'=(x+y)',
∴2
xy·ln2·(xy)'=1+y',
∴2
xyln2·(y+y')=1+y',
y·2
xy·ln2+x·2
xyln2·y'=1+y',
y'(x·2
xyln2-1)=1-y·2
xyln2,
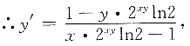
∴y'(0)=y(0)2
0ln2-1=ln2·y(0)-1,
又将x=0代入原式得:2
0=y(0),∴y(0)=1.
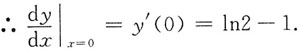
4. 求函数y=x
sinx(x>0)的导数.
[解析] ∵lny=lnx
sinx,∴lny=sinxlnx,两边求导得
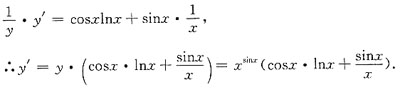
5.
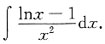
[解析]

7. 求由方程e
z-xyz=0所确定的二元函数z=f(x,y)的全微分dz.
[解析] 令F(x,y,z)=e
z-xyz,则F
x(x,y,z)=-yz,
F
y(x,y,z)=-xz,F
z(x,y,z)=e
z-xy,
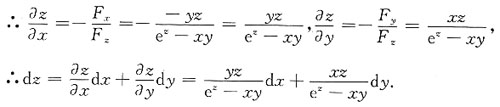
8. 求微分方程
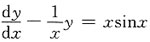
的通解.
[解析] 该微分方程所对应的齐次方程为
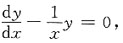
分离变量得:
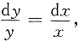
∴lny=lnx+lnC=lnCx.
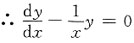
的通解为:y=Cx,
设原方程所对应的通解为y=C(x)x,
∴y'=C'(x)x+C(x),
代入原方程得:
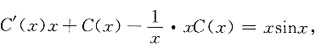
∴C'(x)=sinx,
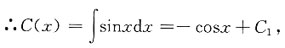
∴原方程的通解为:y=(-cosx+C
1)x,C
1为任意常数.
9. 求平行于y轴且过点P(1,-5,1)和Q(3,2,-1)的平面方程.
[解析] ∵y轴的方向向量a={0,1,0},
设平面的法向量为n={A,B,C},
则A×0+B×1+C×0=0,
∴B=0.
∴设平面方程为Ax+Cz+D=0.
∵平面过点P(1,-5,1)和Q(3,2,-1),
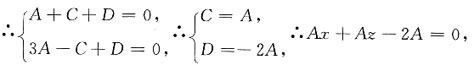
∴该平面的方程为x+z-2=0.
10. 求
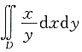
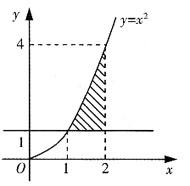
,其中D是由y=1,y=x
2,x=2围成的闭区域.
[解析]
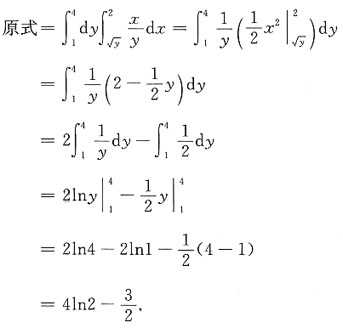
四、应用和证明题(每小题10分,共20分)
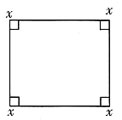
1. 现有边长为96厘米的正方形纸板,将其四角各剪去一个大小相同的小正方形,折做成无盖纸箱,问剪区的小正方形边长为多少时做成的无盖纸箱的容积最大?
[解析] 设剪去的小正方形的边长为xcm,则纸箱的底面边长为96-2x,高为x,容积V=(96-2x)
2·x,
∴V'=2(96-2x)·(96-2x)'·x+(96-2x)
2 =-4x(96-2x)+(96-2x)
2 =(96-2x)(96-6x),
令V'=0得x
1=16,x
2=48(舍),由于实际问题最大值一定存在,
∴当剪去的小正方形的边长为16cm时,纸箱的容积最大.
2. 设函数f(x)在[0,1]上连续,并且对于[0,1]上的任意x所对应的函数值f(x)均有0≤f(x)≤1,证明:在[0,1]上至少有一点ξ,使得f(ξ)=ξ.
[证明] 令G(x)=f(x)-x,
∵f(x)在[0,1]上连续,
∴G(x)在[0,1]上连续.
∵对
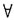
x∈[0,1]均有0≤f(x)≤1,
∴0≤f(0)≤1,0≤f(1)≤1,
∴G(0)=f(0)-0=f(0)≥0,G(1)=f(1)-1≤0,
∴由零点定理知,至少存在一点ξ∈[0,1]使得G(ξ)=0,即f(ξ)-ξ=0,
∴在[0,1]上至少有一点ξ,使得f(ξ)=ξ.