银符考试题库B12
现在是:
试卷总分:150.0
您的得分:
考试时间为:
点击“开始答卷”进行答题
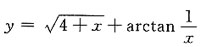 的定义域是______
的定义域是______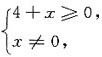 解得x≥-4且x≠0,应选C.
解得x≥-4且x≠0,应选C.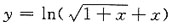
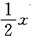
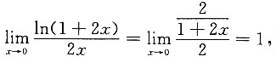 所以当x→0时2x与ln(1+2)等价.
所以当x→0时2x与ln(1+2)等价.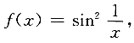 则x=0是f(x)的______
则x=0是f(x)的______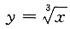 在点x=0处______
在点x=0处______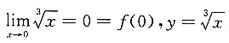 在x=0处连续,又
在x=0处连续,又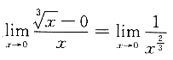 不存在,故
不存在,故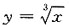 在x=0处不可导,应选C.
在x=0处不可导,应选C.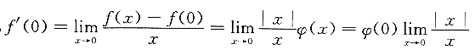 因φ(0)≠0,故f'(0)不存在,应选A.
因φ(0)≠0,故f'(0)不存在,应选A.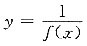 有水平渐近线的充分条件______
有水平渐近线的充分条件______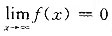
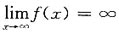
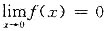
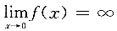
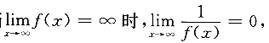 由此可得y=0是
由此可得y=0是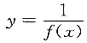 的水平渐近线,应选B.
的水平渐近线,应选B.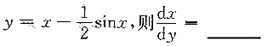
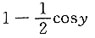
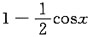
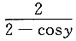
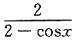
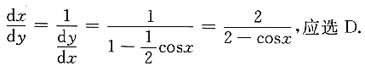
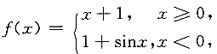 在点(0,1)处的切线斜率是______
在点(0,1)处的切线斜率是______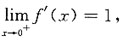 当x<0时
当x<0时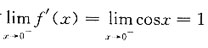 故f'(0)=1,应选B.
故f'(0)=1,应选B.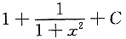
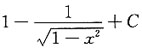
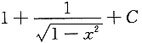
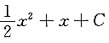
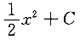
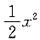 +x+C,应选B.
+x+C,应选B.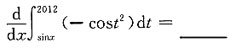
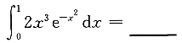
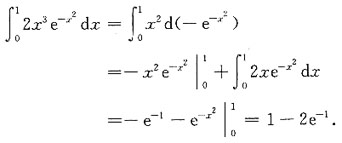
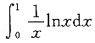

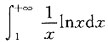
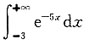
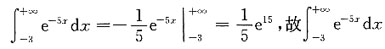 收敛,A,B,C选项均发散,应选D.
收敛,A,B,C选项均发散,应选D.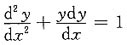 是______
是______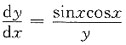 的通解是______
的通解是______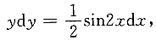 两边积分得
两边积分得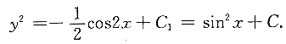
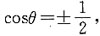 θ=60°或120°,应选D.
θ=60°或120°,应选D.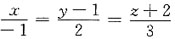 与平面2x+y=0的位置关系是______
与平面2x+y=0的位置关系是______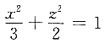
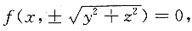 所以选项C符合题意,其他选项不合题意,应选C.
所以选项C符合题意,其他选项不合题意,应选C.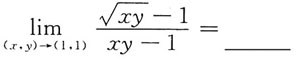
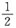
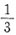
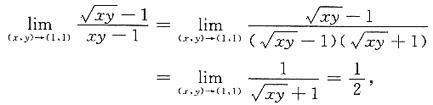 应选B.
应选B.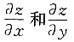 存在的______
存在的______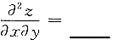
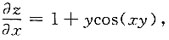
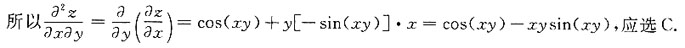
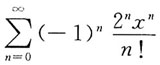 的和函数S(x)为______
的和函数S(x)为______
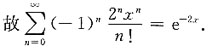
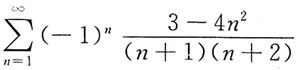
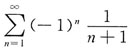
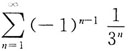
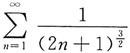
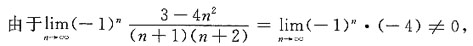
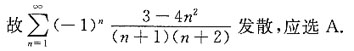
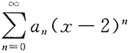 在点x=0处条件收敛,则在x=-1,x=2,x=3,x=4,x=5中使该级数一定收敛的点有______
在点x=0处条件收敛,则在x=-1,x=2,x=3,x=4,x=5中使该级数一定收敛的点有______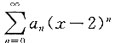 在x=0处条件收敛,故此级数在|x-2|<2时绝对收敛,在|x-2|>2时发散,即在x=2,x=3处收敛,在x=-1,x=5时发散,x=4时的敛散性不能确定,故应选C.
在x=0处条件收敛,故此级数在|x-2|<2时绝对收敛,在|x-2|>2时发散,即在x=2,x=3处收敛,在x=-1,x=5时发散,x=4时的敛散性不能确定,故应选C.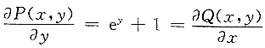 ,故此曲线积分与路径无关,取由点(1,1)经过点(1,-1)到点(-1,-1)折线段上的积分.
,故此曲线积分与路径无关,取由点(1,1)经过点(1,-1)到点(-1,-1)折线段上的积分.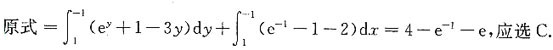
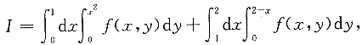 则交换积分次序后,I可化为______
则交换积分次序后,I可化为______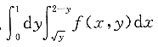
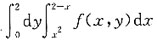
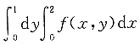
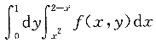
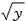 ≤x≤2-y},所以改变积分次序后
≤x≤2-y},所以改变积分次序后 ,应选A.
,应选A.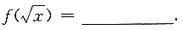
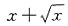
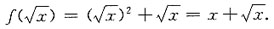
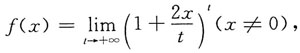 则f(ln2)=______.
则f(ln2)=______.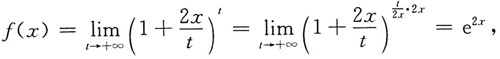
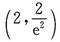
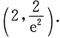
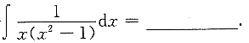
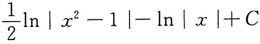

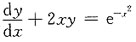 满足y(0)=0的特解为______.
满足y(0)=0的特解为______.
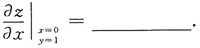
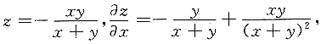

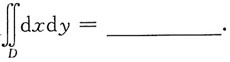
 即为积分区域的面积,所以
即为积分区域的面积,所以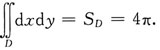
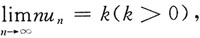 则正项级数
则正项级数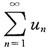 的敛散性为______.
的敛散性为______.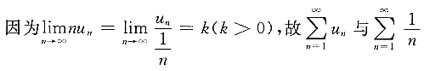 具有相同的敛散性,所以
具有相同的敛散性,所以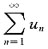 发散.
发散.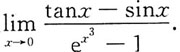
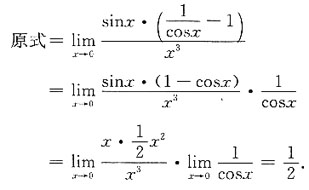
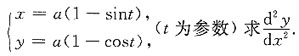
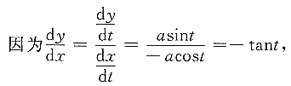
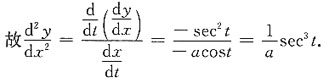
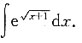
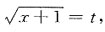 则x=t2-1,且dx=2tdt,
则x=t2-1,且dx=2tdt,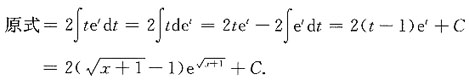
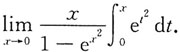
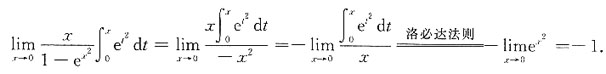
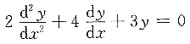 的通解.
的通解.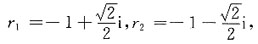
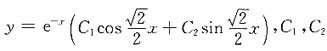 为任意常数.
为任意常数.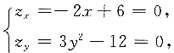 解得驻点(3,2),(3,-2),
解得驻点(3,2),(3,-2),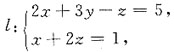 平行的直线方程.
平行的直线方程.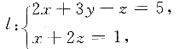
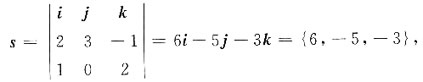
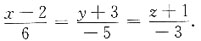
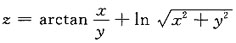 的全微分.
的全微分.
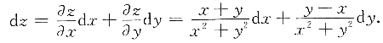
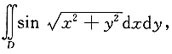 其中D为圆环:π2≤x2+y2≤4π2.
其中D为圆环:π2≤x2+y2≤4π2.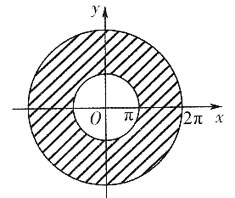
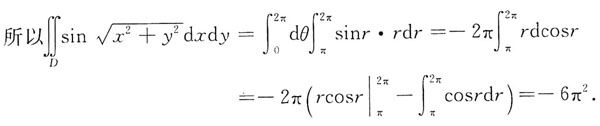
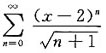 的收敛域.
的收敛域.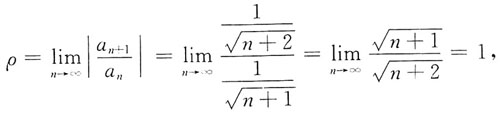 故收敛半径为
故收敛半径为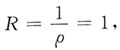
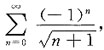 因为
因为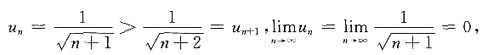 所以收敛,
所以收敛,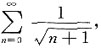 发散,
发散,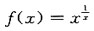 在x>0时的最大值,并从数列
在x>0时的最大值,并从数列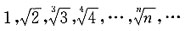 中选出最大的一项(已知
中选出最大的一项(已知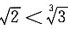 ).
).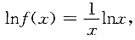 两边对x求导得
两边对x求导得
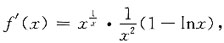 令f'(x)=0,解得驻点x=e.
令f'(x)=0,解得驻点x=e.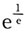 .
.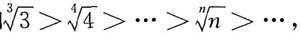 已知
已知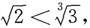 所以
所以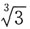 是此数列中最大的一项.
是此数列中最大的一项.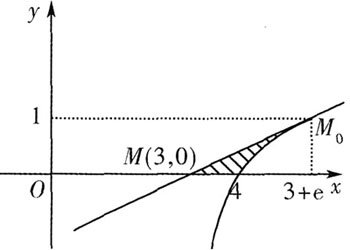
 所以切线方程为
所以切线方程为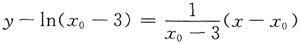 ,因为切线经过点M(3,0),所以将M(3,0)代入上式得x0=e+3,从而切线方程为
,因为切线经过点M(3,0),所以将M(3,0)代入上式得x0=e+3,从而切线方程为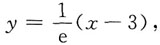
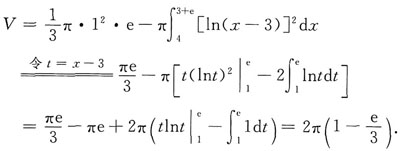
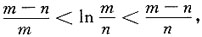 其中n<m为正整数.
其中n<m为正整数.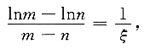
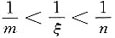 ,从而有
,从而有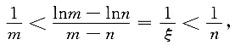 整理得
整理得
