单项选择题(下列选项中,只有一项符合题意)
2. 设函数f(x)在x=a的某个邻域内连续,且f(a)为其极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有
。

A B C D
C
[解析] 利用极大值的定义讨论即可。
由题设,存在邻域(a-δ,a+δ),使当x∈(a-δ,a+δ)时,有f(x)≤f(a),所以
当a-δ<x<a时,(x-a)[f(x)-f(a)]≥0;
当a<x<a+δ时,(x-a)[f(x)-f(a)]≤0。
因此AB两项不成立。
考虑到CD两项中分母均大于零,而分子部分有
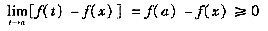
所以必有C项成立。
3. 设y=f(x)是满足微分方程y"+y'-e
sinx=0的解,且f'(x
0)=0,则f(x)在
。
- A.x0的某个邻域内单调增加
- B.x0的某个邻域内单调减少
- C.x0处取得极小值
- D.x0处取得极大值
A B C D
C
[解析] 将f'(x
0)=0代入方程得f"(x
0)的符号,从而由极值的充分条件得正确选项。
f(x)满足方程f"(x)+f'(x)-e
sinx=0,所以有
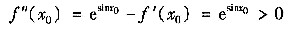
即 f'(x
0)=0,f"(x
0)>0
故f(x)在x
0处取得极小值。
4. 设随机变量X~N(μ,1
2),Y~χ
2(n),且X与Y相互独立,
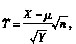
则下列结论正确的是
。
- A.T服从t(n-1)分布
- B.T服从t(n)分布
- C.T服从正态分布N(0,1)
- D.T服从F(1,n)分布
A B C D
B
[解析] 由X~N(μ,1
2),则
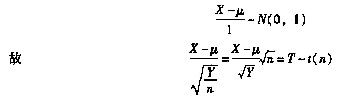
5. 二元函数f(x,y)在点(x
0,y
0)处两个偏导数f'
x(x
0,y
0)、f'
y(x
0,y
0)存在是f(x,y)在该点连续的
。
- A.充分条件而非必要条件
- B.必要条件而非充分条件
- C.充分必要条件
- D.既非充分条件又非必要条件
A B C D
B
[解析] 用反例进行说明:例如
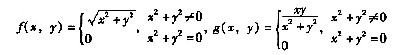
可以验证:
f(x,y)在点(0,0)连续,但f'
x(0,0),f'
y(0,0)均不存在;
g(x,y)在点(0,0)处g'
x(0,0),g'
y(0,0)均存在,但不连续。
因此是既非充分条件又非必要条件。
11. 过点P(1,0,1)且与两条直线L
1:
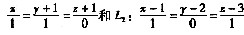
都相交的直线的方向向量可取为
。
- A.(-1,1,2)
- B.(-1,1,-2)
- C.(1,1,-2)
- D.(1,1,2)
A B C D
D
[解析] 设过点P(1,0,1)的直线,L分别与直线L
1与L
2交于点A和点B,由L
1和L
2的方程知,存在常数λ使点A的坐标为(λ,λ-1,-1),存在常数μ使点B的坐标为(1+μ,2,3+μ),

即:
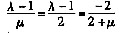
由此可求得λ=0,μ=2,即点A为(0,-1,-1),点B为(3,2,5)。从而,直线L的方向向量可取任一平行于
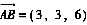
的非零向量。
15. 设总体X服从正态N(μ,σ
2)分布,X
1,X
2,X
3,…,X
n是来自正态总体X的样本,
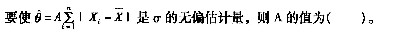
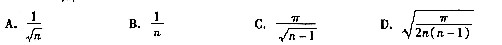
A B C D
D
[解析] 依题意知X
i~N(μ,σ
2)且棚互独立,i=1,2,…,n
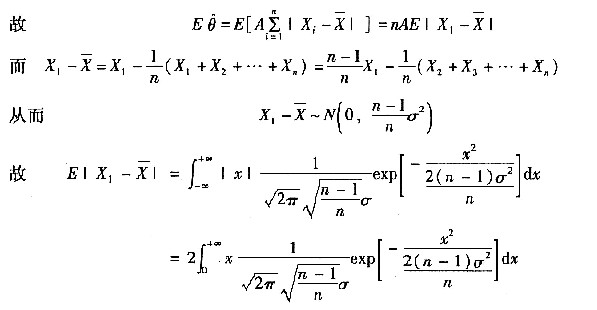
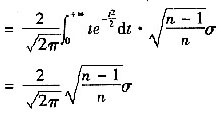
因此有
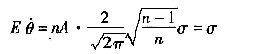
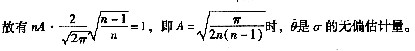
16. 求极限
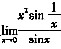
时,下列各种解法中正确的是
。
A.用洛必达法则后,求得极限为0
B.因为
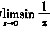
不存在,所以上述极限不存在
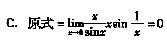
D.因为不能用洛必达法则,故极限不存在
A B C D
A
[解析] A项,

不存在,故不能用洛比达法则求极限。
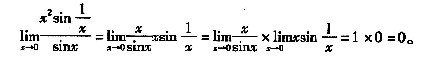
21. 设向量组α
1,α
2,α
3线性无关,则下列向量组中,线性无关的是
。
- A.α1+α2,α2+α3,α3-α1
- B.α1+α2,α2+α3,α1+2α2+α3
- C.α1+2α2,2α2+3α3,3α3+α1
- D.α1+α2+α3,2α1-3α2+22α3,3α1+5α2-5α3
A B C D
C
[解析] A项,(α
1+α
2)-(α
2+α
3)+(α
3-α
1)=0;
B项,(α
1+α
2)+(α
2+α
3)-(α
1+2α
2+α
3)=0;
可见AB两项中向量组线性相关,CD两项不能直接观察出,对于C项,令
k
1(α
1+2α
2)+k
2(2α
2+3α
3)+k
3(3α
3+α
1)=0
即 (k
1+k
3)α
1+(2k
1+2k
2)α
2+(3k
2+3k
3)α
3=0
由于α
1,α
2,α
3线性无关,故

k
1=k
2=k
3=0,故C项中量纰线性无关。
[评注] 判断一个向量组足否线性相关常转化为判断一个齐次线性方程组是否有非零解。
24. 设f(x,y,z)是连续函数,
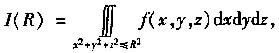
则R→0时,下面说法正确的是
。
- A.I(R)是R的一阶无穷小
- B.I(R)是R的二阶无穷小
- C.I(R)是R的三阶无穷小
- D.I(R)至少是R的三阶无穷小
A B C D
D
[解析] f(x,y,z)为常数M时,
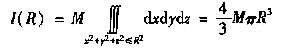
对任意连续函数f(x,y,z),则由积分中值定理得:
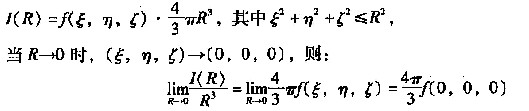
当f(0,0,0)≠0时,I(R)是R的三阶无穷小,当f(0,0,0)=0时,I(R)是比R
3高阶的无穷小。
27. 设a,b,c为非零向量,则与a不垂直的向量是
。
A.(a·c)b-(a·b)c
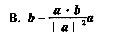
C.a×b D.a+(a×b)×a
A B C D
D
[解析] 由两向量垂直的充要条件:两向量的数量积为零,以及由向量的运算法则有
A项,a·[(a·c)b-(a·b)c]=0;
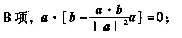
C项,a·(a×b)=0;
D项,a·[a+(a×b)×a]=|a|
2≠0。
28. 齐次线性方程组
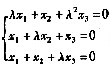
的系数矩阵记为A。若存在三阶矩阵B≠O使得AB=O,则
。
- A.λ=-2且|B|=0
- B.λ=-2且|B|≠0
- C.λ=1且|B|=0
- D.λ=1且|B|≠0
A B C D
C
[解析] 由题设条件:AB=O,且B≠0知方程组Ax=0存在非零解,于是|A|=0,即
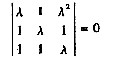
解得λ=1。
于是
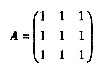
由AB=O,知B
TA
T=O。
故方程组B
Tx=0存在非零解,于是|B|=|B
T|=0。
[解析2]因为AB=O,所以r(A)+r(B)≤3,
又A≠O,B≠O,
所以1≤r(A)<3,1≤r(B)<3,
故 |B|=0。
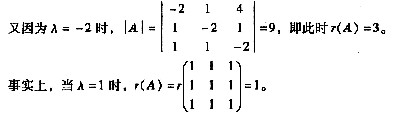
31. 设α
1,α
2,α
3,β
1,β
2,均为4维列向量,A=(α
1,α
2,α
3,β
1),B=(α
3,α
1,α
2,β
2),且|A|=1,|B|=2。则|A+B|=
。
A B C D
B
[解析] |A+B|=|α1+α3,α2 α1,α3+α2,β1+β2|
=|2(α1+α2+α3),α2+α1,α3+α2,β1+β2|
=2|α1+α2+α3,α2+α1,α3+α2,β1+β2|
=2|α1+α2+α3,-α3,-α1,β1+β2|
=2|α2,-α3,-α1,β1+β2|
=2|α1,α2,α3,β1+β2|
=2(|A|+|B|)=6
33. 设f(x)的二阶导数f"(x)存在,则求极限
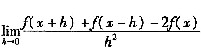
正确的方法是
。
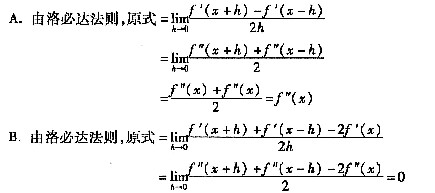
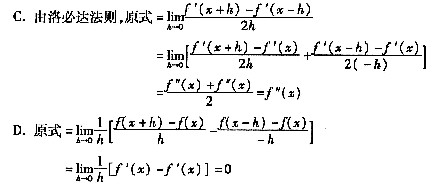
A B C D
C
[解析] A项,题设只说明f"(x)存在,并未说明f"(x)连续,所以等式
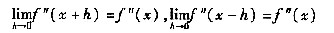
皆未必成立。
B项,此极限中,h是变量,而x是不变量,故使用洛必达法则时,分子、分母均应对变量h求导。此解错在分子是对x求导,而分母是对h求导。
D项,这种解法运用的是乘积的求极限法则,但因
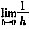
不存在,故不能使用乘积的求极限法则。
C项,符合导数的定义。
35. 设函数
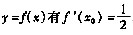
,则当△x→0时,该函数在x=x
0处的微分dy是
。
- A.与△x等价的无穷小
- B.与△x同阶的无穷小,但不等价
- C.比△x低阶的无穷小
- D.比△x高阶的无穷小
A B C D
B
[解析] 据微分概念及同阶无穷小的定义,因

故
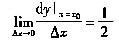
即dy与△x为同阶无穷小,但不等价。
37. 曲线
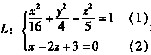
在xOy面上的投影柱面方程是
。

A B C D
A
[解析] 投影柱面方程是一个二元方程,C、D表示的是曲线。而B中的方程中含z,不可能是L在xOy面上的投影柱面方程。
[解析2]由(2)得
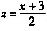
,代入(1)化简得:x
2+20y
2-24x-116=0,为L在xOy面上的投影柱面方程。
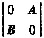 等于 。
等于 。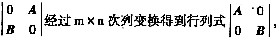


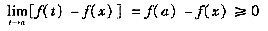
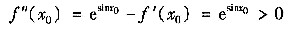
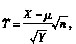 则下列结论正确的是 。
则下列结论正确的是 。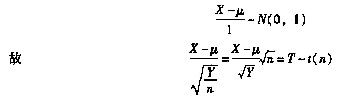
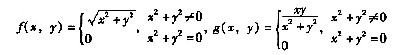
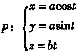 (a,b为正常数)上任一点处的切线 。
(a,b为正常数)上任一点处的切线 。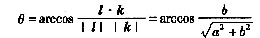
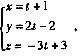 则该直线 。
则该直线 。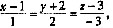 则直线的方向向量为±(1,2,-3),过点(1,-2,3)。
则直线的方向向量为±(1,2,-3),过点(1,-2,3)。 的平面方程为( )。
的平面方程为( )。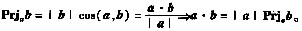
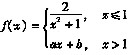 可导,则必有( )。
可导,则必有( )。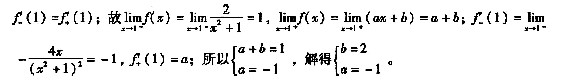
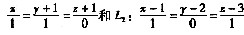 都相交的直线的方向向量可取为 。
都相交的直线的方向向量可取为 。 即:
即: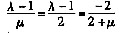
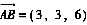 的非零向量。
的非零向量。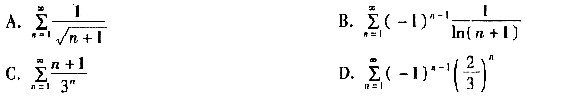
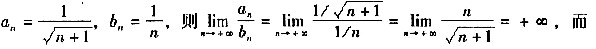
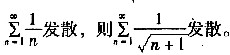 根据交错级数判别法,可以判定B、D是收敛的;C项足正项级数,根据根值判别法可以判定C也是收敛的。
根据交错级数判别法,可以判定B、D是收敛的;C项足正项级数,根据根值判别法可以判定C也是收敛的。
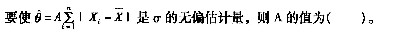
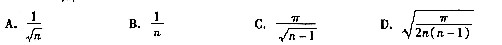
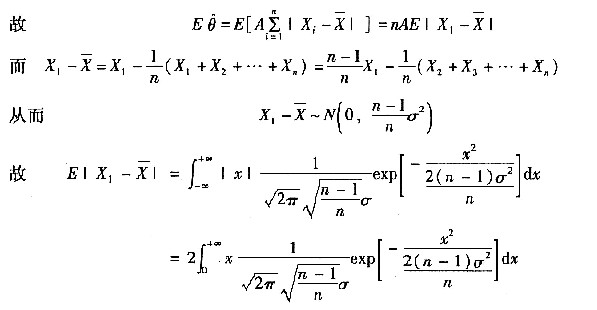
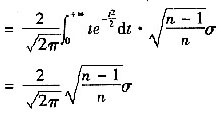
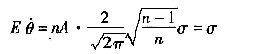
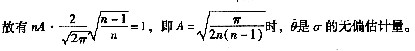
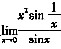 时,下列各种解法中正确的是 。
时,下列各种解法中正确的是 。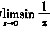 不存在,所以上述极限不存在
不存在,所以上述极限不存在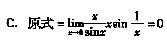
 不存在,故不能用洛比达法则求极限。
不存在,故不能用洛比达法则求极限。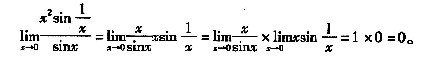
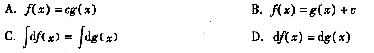
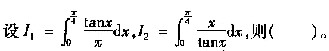
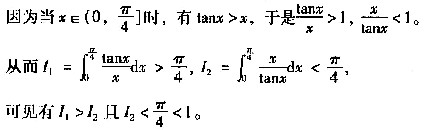

 之间关系是 。
之间关系是 。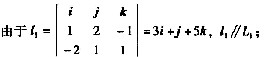
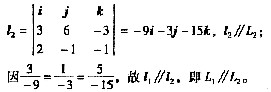

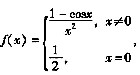 则f(x)在x=0点6阶导数f(6)(0)是 。
则f(x)在x=0点6阶导数f(6)(0)是 。
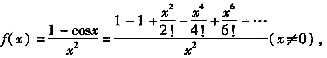
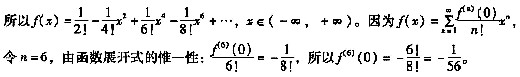
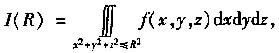 则R→0时,下面说法正确的是 。
则R→0时,下面说法正确的是 。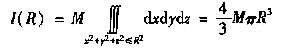
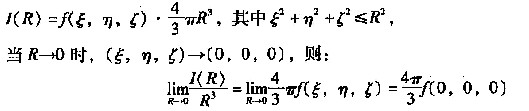
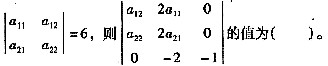
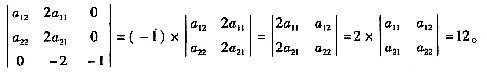

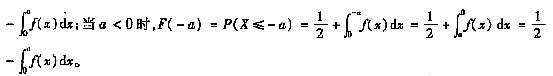
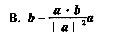
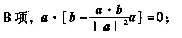
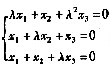 的系数矩阵记为A。若存在三阶矩阵B≠O使得AB=O,则 。
的系数矩阵记为A。若存在三阶矩阵B≠O使得AB=O,则 。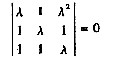
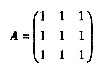
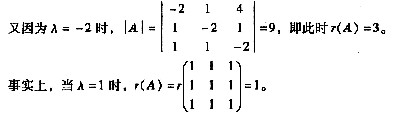
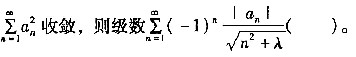

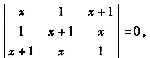 则实数x的值为 。
则实数x的值为 。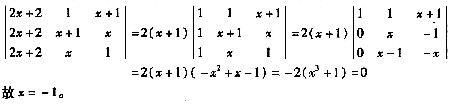
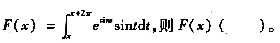

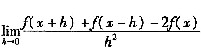 正确的方法是 。
正确的方法是 。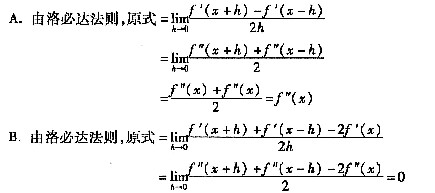
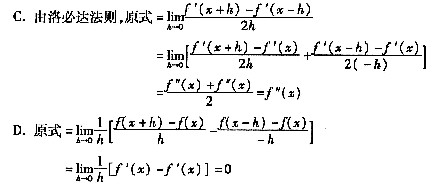
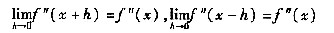
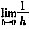 不存在,故不能使用乘积的求极限法则。
不存在,故不能使用乘积的求极限法则。
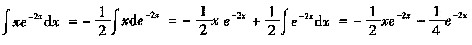
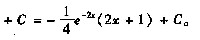
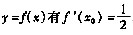 ,则当△x→0时,该函数在x=x0处的微分dy是 。
,则当△x→0时,该函数在x=x0处的微分dy是 。
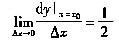
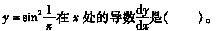

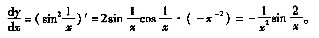
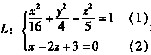 在xOy面上的投影柱面方程是 。
在xOy面上的投影柱面方程是 。
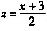 ,代入(1)化简得:x2+20y2-24x-116=0,为L在xOy面上的投影柱面方程。
,代入(1)化简得:x2+20y2-24x-116=0,为L在xOy面上的投影柱面方程。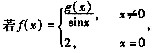 则 。
则 。
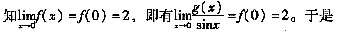
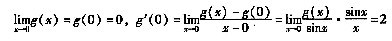

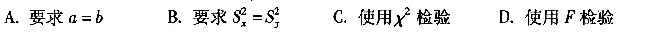
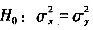 使用F检验,检验的统计量
使用F检验,检验的统计量

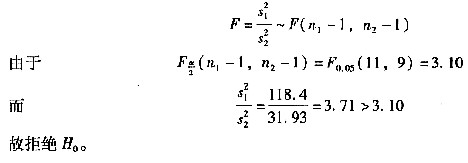

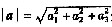 分别验证。
分别验证。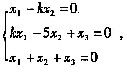 当方程组有非零解时,k值为 。
当方程组有非零解时,k值为 。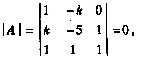 k2-k-6=0,所以k=3或k=-2。
k2-k-6=0,所以k=3或k=-2。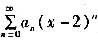 在x=-2时条件收敛,则埘于此幂级数的收敛半径R 。
在x=-2时条件收敛,则埘于此幂级数的收敛半径R 。
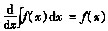 ,有不定积分是微分的逆运算,故d∫f(x)dx=f(x)dx成立。
,有不定积分是微分的逆运算,故d∫f(x)dx=f(x)dx成立。