第Ⅰ部分 选择题
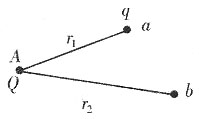
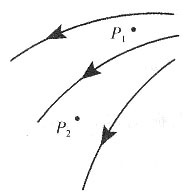
一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)4. 如下图所示,带电量为Q的点电荷位于A点,将另一带电量为q的点电荷从a点移到b点。a、b两点到A点的距离分别为r
1和r
2,则移动过程中电场力所做的功为______
A.
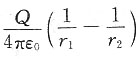
B.
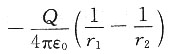
C.
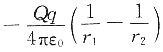
D.
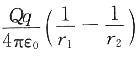
A B C D
D
[考点] 本题主要考查的知识点为电场力做功。
[解析] 电场力所做的功
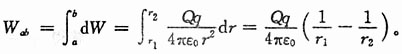
8. 有两个沿z轴做简谐振动的质点,其频率、振幅相同,当第一个质点在平衡位置x=0处向负方向运动时,第二个质点在
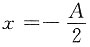
处(A为振幅)也向负方向运动,则两者的相位差φ
2-φ
1为______
A.

B.
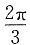
C.
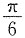
D.
A B C D
C
[解析] 根据简谐振动的旋转矢量法可知,题干中两者的相位差
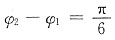
。
10. 在匀强磁场中,有两个平面线圈,其面积A
1=2A
2,通有电流I
1=2I
2,则它们所受的最大磁力矩之比M
1/M
2等于______
A B C D
C
[考点] 本题主要考查的知识点为磁力矩公式的应用。
[解析] 根据磁力矩公式M=BISsinφ最大磁力矩就是φ=90°时M=BIS因为A
1=2A
2,I
1=2I
2所以
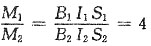
16. 一平面简谐波沿x轴传播,已知在x
1=2m处质元的振动方程为
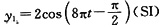
;在x
2=3m处质元的振动方程为
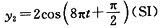
;x
2-x
1<λ(λ为波长,则该平面波的波长为______
A B C D
D
[解析] 利用波程差公式
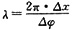
,其中
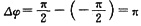
,Δx=3-2=1m,所以λ=2m。答案为D。
19. 已知有同方向的两简谐振动,它们的运动方程分别为x
1=5cos(10t+0.75π)cm,x
2=6cos(10t+0.25π)cm,则合振动的振幅为______。
A.

B.
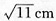
C.11cm
D.61cm
A B C D
A
[考点] 本题主要考查的知识点为合振动的振幅的计算方法。
[解析] 合振动的振幅
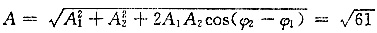
。
20. 一长为L(质量可略)的直杆,两端各固定有质量2m和m的小球,杆可绕通过其中点O与杆所在平面垂直的光滑固定轴在铅直平面内转动,初始时杆与水平方向成θ角,静止。释放后,当杆转到水平位置时,该角加速度的大小α=______
A.
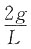
B.
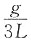
C.
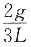
D.
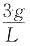
A B C D
C
[考点] 本题主要考查的知识点为刚体的定轴转动定律。
[解析]
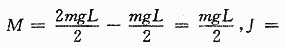
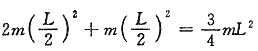
则

第Ⅱ部分 非选择题
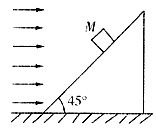
二、填空题1. 如图所示,质量为M的物体位于倾角为45°的固定光滑斜面上,设对物体施加一个水平向有的恒力,其大小和物体所受的重力的大小相等,则物体的加速度a=______m/s
2。
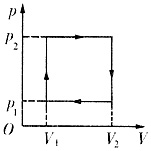
2. 气体经历如图所示的循环过程。在一次循环中,气体对外所做的净功是______。
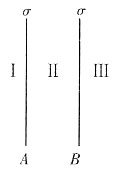
3. 如图,真空中两无限大平行平面A和B均匀带电,电荷面密度都是σ,则在Ⅱ区中的电场强度大小为E
Ⅱ=______。
4. 某射线中的介子在自身参考系中固有寿命是T
0,其相对论动能是静止能量的6倍,则其在实验室参考系中的寿命是______。
7T0
[考点] 本题主要考查的知识点为狭义相对论的时空观及时间延缓效应。
[解析]
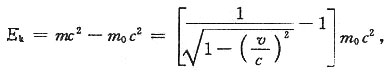
由题意
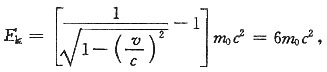
所以

时间延缓效应,
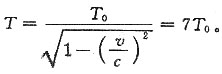
5. 某一质点沿Ox轴作直线运动,它的运动方程为:x=4+5t+6t
2(式中位移单位为m,时间单位为s),则该质点在初时刻(即t=0的时刻)的速度等于______。
5m/s
[考点] 本题主要考查的知识点是运动学第一类问题已知r和初始条件求v。
[解析] 对x=4+5t+6t2上式求导得v=5+12t将t=0代入可得v=5m/s。
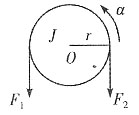
6. 如图,不可伸长的轻绳绕过一半径为r、转动惯量为J的定滑轮,绳和定滑轮之间无相对滑动,轮轴光滑。轻绳两端的张力大小分别为F
1和F
2且F
1>F
2,则滑轮的角加速度大小α=______。
三、计算题(每小题10分,共30分。要写出主要的解题过程。只有答案,没有任何说明和过程,无分。)1. 1mol刚性分子理想气体经历如下图所示的过程,其中1→2是等压过程,2→3是等体过程,3→1是等温过程。试分别讨论在这三个过程中,气体吸收的热量、对外所做的功以及气体热力学能的增量是大于、小于还是等于零。

解:(1)1→2是等压过程。因为V
2>V
1,根据理想气体物态方程,得到T
2>T
1。因此,对1mol的理想气体有
Q=G
p,m(T
2-T
1)>0
W
p=p(V
2-V
1)=R(T
2-T
1)>0
ΔU=C
v,m(T
2-T
1)>0
Q
p、W
p、ΔU都大于零,表明在过程1→2中,气体从外界吸收的热量一部分用了对外做功,其余部分用来增加热力学能。
(2)2→3是等体过程,故气体不做功,即W
v=0
从p-V图上看出,此过程中气体的压强变小,根据理想气体物态方程,气体的温度降低,即T
3<T
2,所以有
Q
v=C
v,m(T
3-T
2)<0
ΔU=Q
v<0
Q
v、ΔU都小于零,表明在过程2→3中,气体向外界放出热量,热力学能减少。
(3)3→1是等温过程,故热力学能不变化,即
ΔU=0
从p-V图上看出,V
3>V
1,故1mol理想气体在等温过程中对外界所做的功等于吸收的热量,即
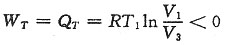
W
T和Q
T小于零,表明在等温过程3→1中,实际上是外界对气体做了正功,同时气体向外界放出热量,使系统热力学能不变。
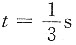 时的波形图如下图所示,且T=2s。求:
时的波形图如下图所示,且T=2s。求:
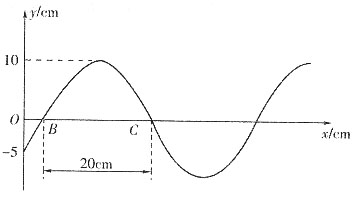
2. 写出原点的振动方程;
解:由波形图可知:A=10cm,λ=40cm,

设原点的振动方程为:
y=Acos(ωt+φ)=10cos(πt+φ)
因为
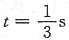
时y=-5,
故
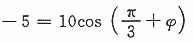
解得:
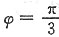
(因为原点向y轴负方向运动,故φ=π舍去)
故原点的振动方程为:
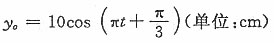
3. 写出该波的波动方程;
解:根据波形图可得波动方程为:
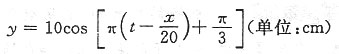
4. 写出C点的振动方程。
解:设C点的振动方程为:
y=10cos(πt+φ
c)
因为

时yc=0,解得
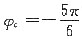
(因为C点向y轴正方向运动,故
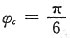
舍去)故C点的振动方程为:
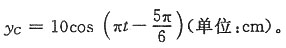

5. 电介质中P点的电势(P点离球心0.3m);
解:
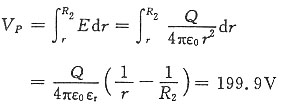
6. 电容器的电容。
解:当P点位于内球表面时,两球的电势差为
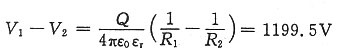
由电容的定义得
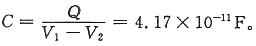
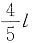
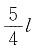
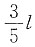
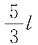
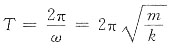 ,仅与弹簧振子的劲度系数k和小球质量m有关,故本题选A。
,仅与弹簧振子的劲度系数k和小球质量m有关,故本题选A。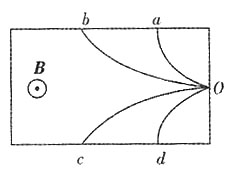
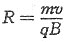 ,q,m,B一定时,R正比于速度v,则可根据半径R大小判断动能的大小。
,q,m,B一定时,R正比于速度v,则可根据半径R大小判断动能的大小。
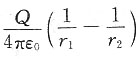
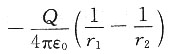
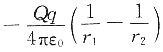
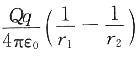
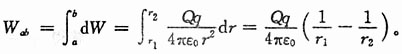
 处(A为振幅)也向负方向运动,则两者的相位差φ2-φ1为______
处(A为振幅)也向负方向运动,则两者的相位差φ2-φ1为______
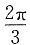
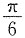
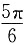
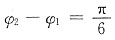 。
。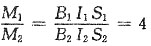
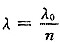 ,其中λ0为真空中的波长,n为介质的折射率;波速ν=νλ,ν不变,λ变小,所以波速也变小。
,其中λ0为真空中的波长,n为介质的折射率;波速ν=νλ,ν不变,λ变小,所以波速也变小。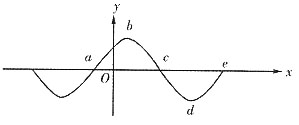
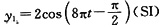 ;在x2=3m处质元的振动方程为
;在x2=3m处质元的振动方程为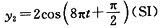 ;x2-x1<λ(λ为波长,则该平面波的波长为______
;x2-x1<λ(λ为波长,则该平面波的波长为______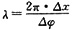 ,其中
,其中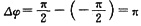 ,Δx=3-2=1m,所以λ=2m。答案为D。
,Δx=3-2=1m,所以λ=2m。答案为D。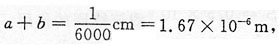 衍射角φ=π/2,代入可得最大k=4。
衍射角φ=π/2,代入可得最大k=4。
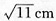
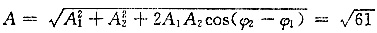 。
。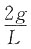
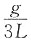
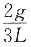
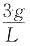
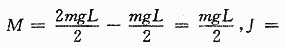
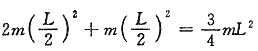



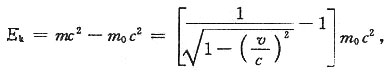
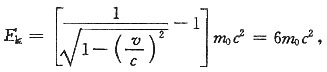

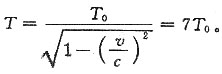
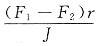

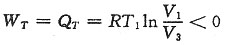
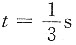 时的波形图如下图所示,且T=2s。求:
时的波形图如下图所示,且T=2s。求:

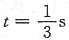 时y=-5,
时y=-5,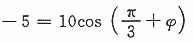
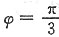 (因为原点向y轴负方向运动,故φ=π舍去)
(因为原点向y轴负方向运动,故φ=π舍去)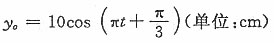
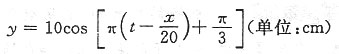
 时yc=0,解得
时yc=0,解得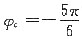 (因为C点向y轴正方向运动,故
(因为C点向y轴正方向运动,故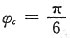 舍去)故C点的振动方程为:
舍去)故C点的振动方程为: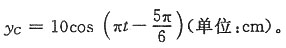

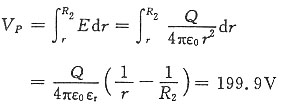
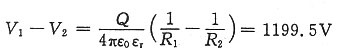
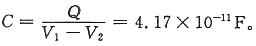
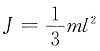 。初始时杆自然悬垂。一质量为m2=1.0×10-2kg的子弹以速率v=4.0×102m/s沿垂直于杆的方向射入杆中点后以速率
。初始时杆自然悬垂。一质量为m2=1.0×10-2kg的子弹以速率v=4.0×102m/s沿垂直于杆的方向射入杆中点后以速率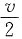 穿出。
穿出。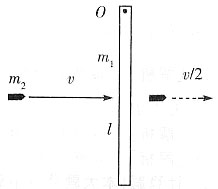
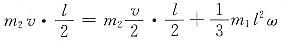
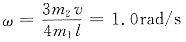
 反弹,杆获得的角速度比上一小问的结果是大还是小?
反弹,杆获得的角速度比上一小问的结果是大还是小?