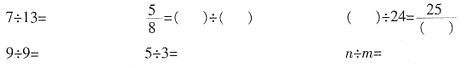一、单项选择题6. 在一次实验中,因测量误差使得三次实验所测的数据按从小到大排列依次为a
1,a
2,a
3,我们规定该实验的最佳实验数据a是这样一个数值,a与各数据a
1,a
2,a
3差的平方和p最小,依此规定,则a为______。
A.
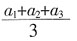
B.
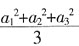
C.a
2 D.p
A B C D
A
[解析] 当a为平均值时,p最小,此时p代表该组数据的方差,表示距离和中心的偏离程度。
7. 若
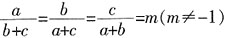
,则关于x的方程
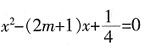
的根的情况是______。
- A.有两个不等的无理数根
- B.有两个相等的无理数根
- C.有两个不等的有理数根
- D.有两个相等的有理数根
A B C D
A
[解析] 由题干等式可知,a=m(b+c),b=m(a+c),c=m(a+b),则a+b+c=2m(a+b+c),由此可知a+b+c=0或2m=1。若a+b+c=0,则

,与题干中m≠-1矛盾,故
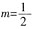
。代入到方程中可得
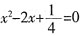
,用公式法解此一元二次方程可得
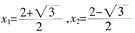
,故此方程有两个不等的无理数根。
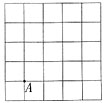
8. 如图,点A是5×5网格图形的一个格点(小正方形的顶点),图中每个小正方形的边长为1,此A为其中一个顶点,面积等于
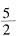
的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是______。
A B C D
C
[解析] 面积为
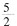
的等腰直角三角形,腰长为
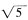
,底边为
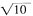
。分两种情况,①当A是等腰直角三角形直角顶点时,以A为圆心
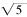
为半径画圆,找到与网格相交于格点的点确定为三角形底边端点,并找到三角形底边另一端点如图1,能找到满足条件的三角形2个;②当A是等腰三角形底边的一个端点时,以A为圆心底边长
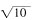
为半径画圆,找到与网格相交于格点的点确定为三角形底边另一端点,并找到等腰直角三角形顶点如图2,能找到满足条件的三角形6个。故选C。
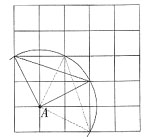 图1
图1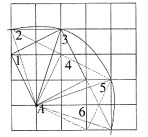 图2
图2
9. 已知f(x)是定义在[-2,0]上的增函数,则满足f(x
2-x-2)>f(1-x)的x的取值范围是______。
A.

B.[1,2]
C.
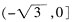
D.
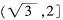
A B C D
D
[解析] f(x)在[-2,0]上单调增,则f(x
2-x-2)>f(1-x)
x
2-x-2>1-x,化简x
2-3>0,解得
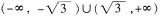
,同时要求-2≤x
2-x-2≤0,解得-1≤x≤0或1≤x≤2;且-2≤1-x≤0,解得1≤x≤3,综上x的取值范围是
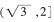
,所以选D。
10. 半径为R的四分之一圆卷成一个圆锥,则它的体积为______。
A.
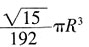
B.
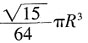
C.
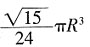
D.
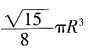
A B C D
A
[解析] 四分之一圆的扇形弧长为
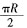
,卷成圆锥底面的半径为
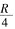
,圆的半径长等于圆锥的母线长,且圆锥底面面积为
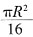
,使用勾股定理求得圆锥的高为

,则圆锥的体积为
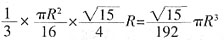
。
二、填空题1. 用0,0,0,0,5,8,7七位数字组成所有0都不读的最小七位数是______。
5007800
[解析] 从右往左数每四位为一级,每级的末尾处的“0”不读,所以可组成最小七位数为5007800。
2. 已知关于x的不等式组
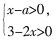
的整数解共有5个,则a的取值范围是______。
4≤a<-3
[解析] 该不等式组的解为

,x有5个整数解,则x可取1,0,-1,-2,-3;由x>a,故-4≤a<-3。
3.
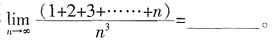
0
[解析]
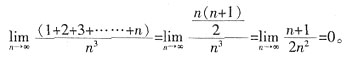
4. 《义务教育数学课程标准(2011年版)》提出,在数学教学活动中,教师需把基本理念转化为自己的教学行为,处理好教师______与学生______的关系,注重启发学生积极思考。
5. 《义务教育数学课程标准(2011年版)》提出,几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的______,预测______。
四、解答题(本题共38分)1. 当母亲的年龄是女儿现在的年龄2倍时,女儿的年龄是母亲现在年龄的
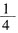
,现在母亲和女儿的年龄之和是68岁,求女儿现在的年龄。
设女儿现在的年龄为x,由题意可知
|
|
女儿
|
母亲
|
| 现在的年龄
|
x
|
68-x
|
| 某年的年龄
|
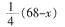
|
2x
|
由于母亲与女儿年龄的差是一定的,故有
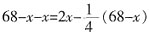
,解得x=20,所以女儿现在的年龄为20岁。
2. 当k=-1时,求出函数f(x)的单调区间;
当k=-1时,则f(x)=-x2(1-x)ex,可求得f'(x)=xex-2x,
令f'(x)=xex-2x>0,解得x<0或x>ln2,此时函数f(x)单调递增;
令f'(x)=xex-2x<0,解得0<x<ln2,此时函数f(x)单调递减;
故函数f(x)的单调递增区间为(-∞,0)和(ln2,+∞),单调递减区间为(0,ln2)。
3. 若函数f(x)在(-∞,-1]上单调递增,求k的取值范围。
对f(x)求导得,f'(x)=xe
x+2kx
若k≥0,令f'(x)=xe
x+2kx>0,则有x>0,不合题意;
若k<0,令f'(x)=xe
x+2kx=0,则x
1=0,x
2=ln(-2k),
当x
2≥x
1时,即
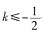
,令f'(x)=xe
x+2kx>0,则有x<0或x>ln(-2k),此时,f(x)在(-∞,-1]为单调递增;
当x
2<x
1时,即
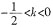
,令f'(x)=xe
x+2kx>0,则有x
0,此时,若使f(x)在(-∞,-1]为单调递增,则需要ln(-2k)≥-1,即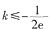 ,所以
,所以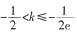 。
。
综上,当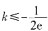 时,f(x)在(-∞,-1]为单调递增。
时,f(x)在(-∞,-1]为单调递增。
4. 求抛物线的方程;
抛物线y
2=2px(p>0)准线方程为
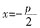
,点A到抛物线准线的距离
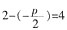
,解得p=4,故抛物线方程为y
2=8x。
5. 已知点Q(-2,0),过抛物线焦点的直线l交抛物线于M,N两点,设直线QM,QN的斜率分别为k
1,k
2,求证k
1+k
2为定值。
抛物线方程为y
2=8x的焦点为(2,0),则过焦点的直线Z方程为y=k(x-2),设直线l与抛物线交于M(x
1,y
1),N(x
2,y
2)。
联立方程
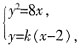
消去y得k
2x
2-(4k
2+8)x+4k
2=0,
由韦达定理得
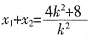
,x
1,x
2=4;
QM的斜率
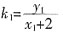
,QK的斜率
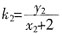
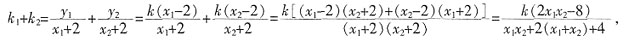
代入x
1x
2=4可知k
1+k
2为定值0。
6. 如图1,求证AC·CB=OC·CP;
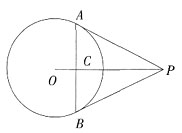 图1
图1
连接OA,OB,PA,PB是圆O的切线,A,B为切点,则有PA=PB,PA⊥OA,PB⊥OB,又OA=OB,则△OAP≌△OBP,故∠APO=∠BPO。
由于PA=PB,故△PAB为等腰三角形,又因为∠APO=∠BPO,所以PC⊥AB,且AC=BC。
在△OAP中,PA⊥OA,PO⊥AC,故有AC2=OC·CP,即AC·CB=OC·CP。
7. 如图2,若过C点的任意直线EF(直线EF不过圆心且不与直线AB重合)交圆O于E,F两点,求证:PO平分∠EPF。
 图2
图2
连接OA,OE,OF。
在△OAP中,PA⊥OA,PO⊥AC,故有△OAC∽△OPA,则
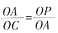
。
在圆中OA,OE均为圆的半径,故OA=OE,即
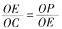
,则有△OEC∽△OPE,进而有∠OEC=∠OPE。
同理可知,∠OFC=∠OPF。
又OE=OF,有∠OEC=∠OFC,所以∠OPE=∠OPF,即PO平分∠EPF。

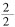 的倒数就不是真分数。
的倒数就不是真分数。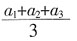
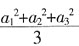
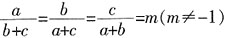 ,则关于x的方程
,则关于x的方程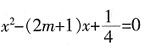 的根的情况是______。
的根的情况是______。 ,与题干中m≠-1矛盾,故
,与题干中m≠-1矛盾,故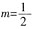 。代入到方程中可得
。代入到方程中可得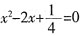 ,用公式法解此一元二次方程可得
,用公式法解此一元二次方程可得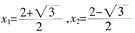 ,故此方程有两个不等的无理数根。
,故此方程有两个不等的无理数根。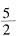 的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是______。
的格点等腰直角三角形(三角形的三个顶点都是格点)的个数是______。
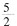 的等腰直角三角形,腰长为
的等腰直角三角形,腰长为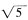 ,底边为
,底边为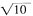 。分两种情况,①当A是等腰直角三角形直角顶点时,以A为圆心
。分两种情况,①当A是等腰直角三角形直角顶点时,以A为圆心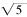 为半径画圆,找到与网格相交于格点的点确定为三角形底边端点,并找到三角形底边另一端点如图1,能找到满足条件的三角形2个;②当A是等腰三角形底边的一个端点时,以A为圆心底边长
为半径画圆,找到与网格相交于格点的点确定为三角形底边端点,并找到三角形底边另一端点如图1,能找到满足条件的三角形2个;②当A是等腰三角形底边的一个端点时,以A为圆心底边长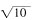 为半径画圆,找到与网格相交于格点的点确定为三角形底边另一端点,并找到等腰直角三角形顶点如图2,能找到满足条件的三角形6个。故选C。
为半径画圆,找到与网格相交于格点的点确定为三角形底边另一端点,并找到等腰直角三角形顶点如图2,能找到满足条件的三角形6个。故选C。


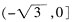
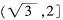
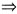 x2-x-2>1-x,化简x2-3>0,解得
x2-x-2>1-x,化简x2-3>0,解得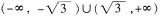 ,同时要求-2≤x2-x-2≤0,解得-1≤x≤0或1≤x≤2;且-2≤1-x≤0,解得1≤x≤3,综上x的取值范围是
,同时要求-2≤x2-x-2≤0,解得-1≤x≤0或1≤x≤2;且-2≤1-x≤0,解得1≤x≤3,综上x的取值范围是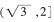 ,所以选D。
,所以选D。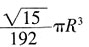
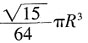
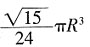
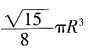
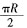 ,卷成圆锥底面的半径为
,卷成圆锥底面的半径为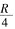 ,圆的半径长等于圆锥的母线长,且圆锥底面面积为
,圆的半径长等于圆锥的母线长,且圆锥底面面积为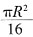 ,使用勾股定理求得圆锥的高为
,使用勾股定理求得圆锥的高为 ,则圆锥的体积为
,则圆锥的体积为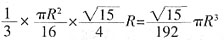 。
。 来说明,还用
来说明,还用 等图示说明,这种教学的活动方式是______。
等图示说明,这种教学的活动方式是______。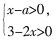 的整数解共有5个,则a的取值范围是______。
的整数解共有5个,则a的取值范围是______。 ,x有5个整数解,则x可取1,0,-1,-2,-3;由x>a,故-4≤a<-3。
,x有5个整数解,则x可取1,0,-1,-2,-3;由x>a,故-4≤a<-3。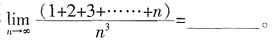
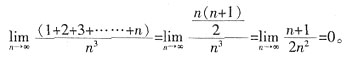
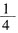 ,现在母亲和女儿的年龄之和是68岁,求女儿现在的年龄。
,现在母亲和女儿的年龄之和是68岁,求女儿现在的年龄。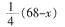
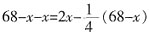 ,解得x=20,所以女儿现在的年龄为20岁。
,解得x=20,所以女儿现在的年龄为20岁。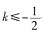 ,令f'(x)=xex+2kx>0,则有x<0或x>ln(-2k),此时,f(x)在(-∞,-1]为单调递增;
,令f'(x)=xex+2kx>0,则有x<0或x>ln(-2k),此时,f(x)在(-∞,-1]为单调递增;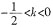 ,令f'(x)=xex+2kx>0,则有x
,令f'(x)=xex+2kx>0,则有x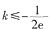 ,所以
,所以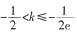 。
。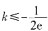 时,f(x)在(-∞,-1]为单调递增。
时,f(x)在(-∞,-1]为单调递增。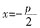 ,点A到抛物线准线的距离
,点A到抛物线准线的距离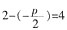 ,解得p=4,故抛物线方程为y2=8x。
,解得p=4,故抛物线方程为y2=8x。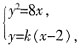 消去y得k2x2-(4k2+8)x+4k2=0,
消去y得k2x2-(4k2+8)x+4k2=0,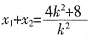 ,x1,x2=4;
,x1,x2=4;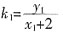 ,QK的斜率
,QK的斜率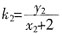
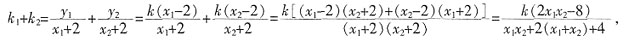


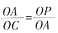 。
。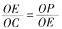 ,则有△OEC∽△OPE,进而有∠OEC=∠OPE。
,则有△OEC∽△OPE,进而有∠OEC=∠OPE。
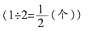
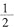 表示的意义吗?这三道题为什么都用除法计算呢?
表示的意义吗?这三道题为什么都用除法计算呢?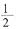 可以表示1÷2的结果,那么分数与除法是不是有联系呢?这节课我们一起学习分数与除法的关系。
可以表示1÷2的结果,那么分数与除法是不是有联系呢?这节课我们一起学习分数与除法的关系。
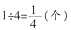
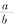 个,即
个,即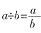 。
。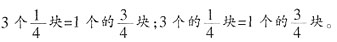
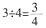 即
即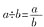 是正确的
是正确的