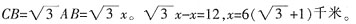第一部分 客观题10. 在实数范围内把2x
2-4x-8分解因式______。
A.2(x-3)(x+1)
B.
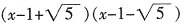
C.
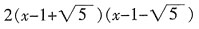
D.

A B C D
C
[解析] 用求根公式法,
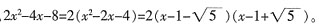
11. 用换元法解方程
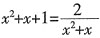
时,若设x
2+x=y,则原方程化为______。
- A.y2+y+2=0
- B.y2-y-2=0
- C.y2-y+2=0
- D.y2+y-2=0
A B C D
D
[解析] 设x
2+x=y,则
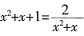
可化为
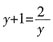
,整理得y
2+y-2=0。
13. 一列火车因事在途中耽误了5分钟,恢复行驶后速度增加5千米/时,这样行驶30千米就将耽误的时间补了回来,若设原来的速度为x千米/时,则所列方程为______。
A.
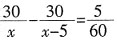
B.
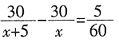
C.
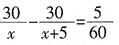
D.
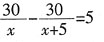
A B C D
C
[解析] 火车原来的速度为x千米/时,提速后的速度为x+5千米/时,由题意,两种速度下行使30千米的时间差为
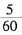
小时,由此可得出方程

14. 已知关于x的方程x
2-mx+m=0的两根平方和是3,则m的值是______。
A B C D
A
[解析] 设两根分别为x
1,x
2,x
1+x
2=m,x
1x
2=
m,

,同时要满足Δ=m
2-4m≥0,故m=-1。
15. 如果关于x的一元二次方程x
2-2(1-m)x+m
2=0的两个实数根为α,β,则α+β的取值范围是______。
A.α+β≥1
B.α+β≤1
C.
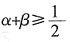
D.
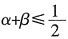
A B C D
A
[解析] 由Δ=4(1-m)2-4m2≥0,得2m≤1,α+β=2-2m,故答案为A。
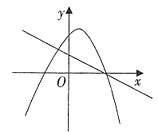
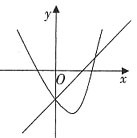
21. 下列各图是在同一直角坐标系内,二次函数y=ax
2+(b+c)x+c与一次函数y=ax+c的大致图象,有且只有一个是正确的,正确的是______。
A.
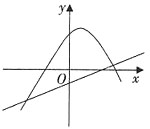
B.
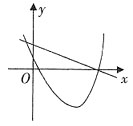
C.
D.
A B C D
D
[解析] 两函数图象都过点(0,c),再验证二次函数的开口方向和一次函数的单调性即可。a<0,则二次函数开口向下,一次函数单调递减;a>0,则二次函数开口向上,一次函数单调递增。只有D项满足。
35. 如果两个相似三角形的面积比是1:2,那么它们的相似比是______。
A.1:2
B.1:4
C.
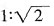
D.2:1
A B C D
C
[解析] 相似三角形面积比是1:2,则相似比为
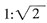
。
36. 设f(x)=lg(10
x+1)+ax是偶函数,
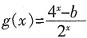
是奇函数,那么a+b的值为______。
A.1 B.-1
C.
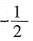
D.
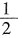
A B C D
D
[解析] 可用特殊值法,f(x)为偶函数,设f(1)=f(-1),可得
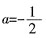
,g(x)为奇函数,则g(0)=0,可得b=1。
37. 已知1是a
2与b
2的等比中项,又是
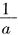
与
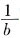
的等差中项,则
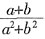
的值是______。
A.
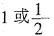
B.
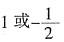
C.
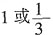
D.
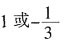
A B C D
39. 已知AD,BE分别是△ABC的边BC,AC上的中线,且
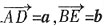
,则
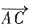
是______。
A.
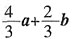
B.
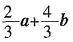
C.
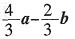
D.
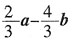
A B C D
A
[解析]
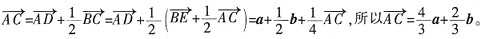
40. 若0<a<1,则下列不等式中正确的是______。
A.
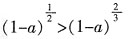
B.log
(1-a)(1+a)>0
C.(1-a)
3>(1+a)
2 D.(1-a)
1+a>1
A B C D
A
[解析] 因为0<a<1,所以0<1-a<1,1+a>1。有(1-a)2>(1-a)3,log(1-a)(1+a)<0,(1-a)3<1<(1+a)2,(1-a)1+a<1。
46. 极限
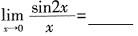
。
A.1
B.2
C.0
D.
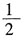
A B C D
B
[解析] 由洛必达法则可得:

50. 在区间(0,+∞)上严格单调增加的函数是______。
A.y=x
3 B.y=tanx
C.y=sinx
D.
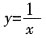
A B C D
A
[解析] 此题考查基本初等函数的图象。tanx的图象只在(0,+∞)的某个小区间上是递增,并且是周期性的,不是严格递增;sinx在(0,+∞)上有递增也有递减;

在(0,+∞)是减函数;只有y=x
3在(0,+∞)是严格递增的,故选A。
一、简答题(每小题6分,共18分)1. 如图,为了测量对岸某建筑物AB的高度,在平地上点C处测得建筑物顶端A的仰角为30°,沿CB方向前进12米到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度(结果保留根号)。
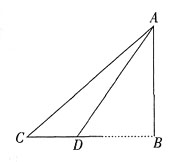
设AB的高度为x,在Rt△ADB中,∠ADB=45°,则DB=AB=x;在Rt△ACB中,∠C=30°,则
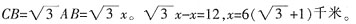
4. 已知函数f(x)=ax
2+bx
2-3x在x=±1处取得极值,讨论f(1)和f(-1)是函数f(x)的极大值还是极小值。
f'(x)=3ax
2+2bx-3
由f(x)在±1处取得极值,故f'(1)=f'(-1)=0,
易得a=1,b=0。
| x
|
(-∞,-1)
|
-1
|
(-1,1)
|
1
|
(1,+∞)
|
| f'(x)
|
+
|
0
|
-
|
0
|
+
|
| f(x)
|
↗
|
极大值
|
↘
|
极小值
|
↗
|
故易得f(-1)是函数f(x)的极大值,f(1)是函数f(x)的极小值。
二、论述题(10分)1. 小学生数学学习的特点是什么?小学数学应用题教学有哪些策略?
小学生数学学习的特点有:①基于学生经验的基础上学习数学;②在多样化的活动中学习数学;③在合作与交流中学习数学;④在解决问题的过程中学习数学;⑤在不同的发展中学习数学。
小学数学应用题教学有如下策略:①认真审题,感知题意;②分析比较,清除障碍;③理清题意,拓展深化;④发散思维,一题多解。
三、案例分析题(12分)1. 以“异分母分数加减”为例,谈谈教师应该怎样进行设问,以改善学生原有的认知结构。
“异分母分数加减”一课的教学重点是让学生理解异分母分数加法和减法的算理,即先通分再计算,以符合相同计数单位相加、减的基本原理。教学难点是理解通分的必要性。数学是一门系统性很强的学科,知识之间有着紧密的联系,旧知是新知的基础,新知是旧知的延伸和发展。在教学新知时,注意在知识的内在联系处设问,有利于学生加深新概念理解,从而改善学生原有的认知结构。在教学异分母分数加减法时,为了使学生透彻地理解先通分、后加减的道理,可拟定如下设问:整数加减法为什么要相同数位对齐?小数加减法为什么要小数点对齐?同分母分数加减法,为什么分子可以直接相加减?异分母分数加减法,为什么分子不能直接相加减?这样的设问,沟通了新旧知识的内在联系,使新知识纳入原有知识系统之中,并且在教师的引导下,学生自己能总结出计算规律。
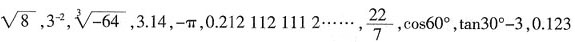 中,无理数有______。
中,无理数有______。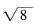 ,-π,0.2121121112……,tan30°-3是无理数。
,-π,0.2121121112……,tan30°-3是无理数。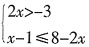 的最小整数解是______。
的最小整数解是______。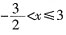 ,最小整数解为-1。
,最小整数解为-1。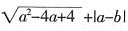 的结果______。
的结果______。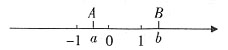
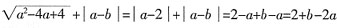 。
。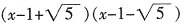
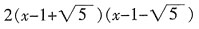

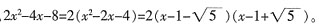
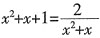 时,若设x2+x=y,则原方程化为______。
时,若设x2+x=y,则原方程化为______。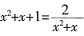 可化为
可化为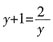 ,整理得y2+y-2=0。
,整理得y2+y-2=0。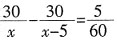
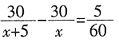
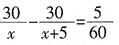
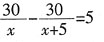
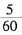 小时,由此可得出方程
小时,由此可得出方程
 ,同时要满足Δ=m2-4m≥0,故m=-1。
,同时要满足Δ=m2-4m≥0,故m=-1。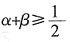
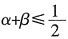
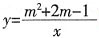 的图象上的一点,则函数图象必须经过点______。
的图象上的一点,则函数图象必须经过点______。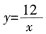 ,满足条件的只有A项。
,满足条件的只有A项。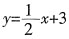 的常数项改为2,那么它的图象是______。
的常数项改为2,那么它的图象是______。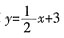 的图象向下平移一个单位或向右平移两个单位,函数变成
的图象向下平移一个单位或向右平移两个单位,函数变成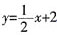 。
。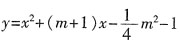 (m为整数)与x轴交于点A,与y轴交于点B,且|OA|=|OB|,则m等于______。
(m为整数)与x轴交于点A,与y轴交于点B,且|OA|=|OB|,则m等于______。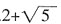
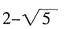




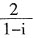 等于______。
等于______。



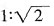
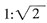 。
。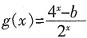 是奇函数,那么a+b的值为______。
是奇函数,那么a+b的值为______。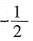
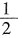
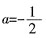 ,g(x)为奇函数,则g(0)=0,可得b=1。
,g(x)为奇函数,则g(0)=0,可得b=1。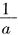 与
与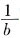 的等差中项,则
的等差中项,则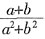 的值是______。
的值是______。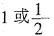
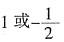
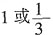
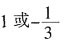
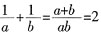 ,所以
,所以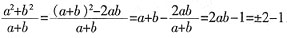 。所以
。所以 或
或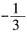 。
。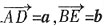 ,则
,则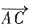 是______。
是______。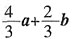
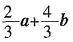
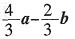
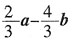
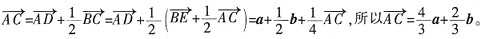
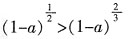
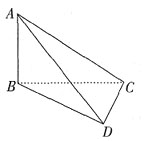
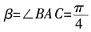 。设AB=1,则
。设AB=1,则 ,所以α<β。
,所以α<β。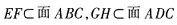 ,又面ABC∩面ADC=AC,所以EF与GH若相交,交点必在直线AC上。
,又面ABC∩面ADC=AC,所以EF与GH若相交,交点必在直线AC上。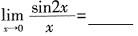 。
。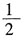

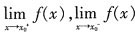 存在且相等是
存在且相等是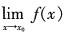 存在的______。
存在的______。 存在的充要条件是
存在的充要条件是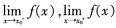 存在且相等。
存在且相等。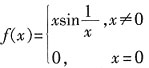 ,则f(x)在x=0处______。
,则f(x)在x=0处______。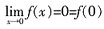 ,即函数f(x)在x=0处连续。极限
,即函数f(x)在x=0处连续。极限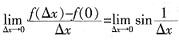 不存在,所以f(x)在点x=0处不可导。
不存在,所以f(x)在点x=0处不可导。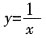
 在(0,+∞)是减函数;只有y=x3在(0,+∞)是严格递增的,故选A。
在(0,+∞)是减函数;只有y=x3在(0,+∞)是严格递增的,故选A。