一、单项选择题2. 下列四个函数中,以π为最小正周期,且在区间
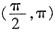
上为减函数的是______。
A.y=cos
2x
B.y=2|sinx|
C.
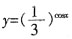
D.y=-cotx
A B C D
B
[解析] A项
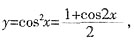
T=π,但在区间
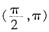
上为增函数。
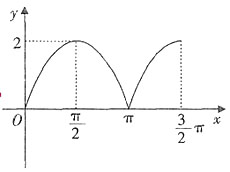
B项:作其图象如下图,由图象可得T=π且在区间
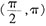
上为减函数。
C项:函数y=cosx在
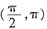
区间上为减函数,函数
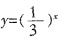
为减函数。因此
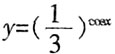
在
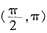
区间上为增函数。
D项:函数y=-cotx在区间
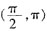
上为增函数。
二、填空题1. f(x)=mx
2-mx-1+x
3除以(x+1)余-2,则实数m为______。
2. 如果从A点向东走50米到B点记作+50米,那么从B点向西走200米应记作______。
-150米
[解析] B点在A点东50米,则由B向西行200米,即为由A点向西行150米,记为-150米。此处,不要忘记带单位。
3. “六一”期间,中央商场搞“家电下乡”活动,农民购买家电时可享受政府补贴13%的优惠政策。张大伯家买了一台电冰箱,只需付1392元,这台冰箱的原价是______元。
1600
[解析] 原价×(1-13%)=1392,可得,原价=1600元。
4. 某商店同时卖出两件商品,每件售价36元,但其中一件赚了25%,另一件亏了25%,则这个商店卖出这两件商品是______(赚或亏)了______元。
亏,4.8元
[解析] 分别以36元价格售出两件商品,一件亏了25%,可得出此件商品亏了
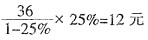
。另一件赚了25%,赚了
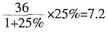
元。故总计亏了4.8元。
5. 大斌今年a岁,小明今年(a-27)岁,再过3年,他们相差______岁。
三、解答题(共52分)1. 某商店到苹果产地收购了2吨苹果,收购价为每千克1.20元,从产地到商店的距离是400千米,运费为每吨货物每运1千米收1.50元,如果在运输及销售过程中的损耗为10%,那么商店要实现15%的利润率,零售价是每千克多少元?
解:设零售价为x元每千克,由题意可得:
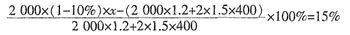
解之得:x=2.3。
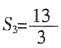 。
。3. 若函数f(x)=Asin(2x+φ)(A>0,0<φ<π)在
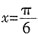
处取得最大值,且最大值为a
3,求函数f(x)的解析式。
由第一小题可知a
n=3
n-2,所以a
3=3,因为函数f(x)的最大值为3,所以A=3;因为当
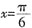
时f(x)取得最大值,所以
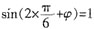
;又0<φ<π,故
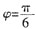
。所以函数f(x)的解析式为
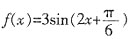
。
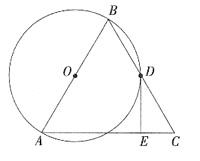
4. 求证:DE是⊙O的切线;
解:证明:如图,连结OD。
∵DE⊥AC,
∴∠DEC=90°。
∴O为AB中点,D为BC中点,
∴OD为△ABC的中位线。
∴OD∥AC。
∴∠ODE=∠DEC=90°。
即OD⊥DE。
∵点D在⊙O上,
∴DE是⊙O的切线。
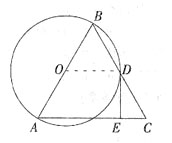
5. 若
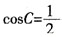
,DE=6,求⊙O的直径。
解:
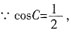
∴∠C=60°。
∵OD∥AC,
∴∠BDO=∠C=60°。
∵OD=OB,
∴∠B=∠ODB=60°。
∴△ABC为等边三角形。
∵在△EDC中,∠DEC=90°,DE=6,
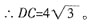
∵D为BC中点,
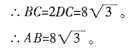
∴⊙O的直径为
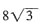
。
6. 如右图,有一条三角形的环路,A至B是上坡路。B至C是下坡路,A至C是平路,A至B、B至C、A至C三段距离的比是3:4:5。李磊和韩梅梅同时从A出发,李磊按顺时针方向行走,韩梅梅按逆时针方向行走,2.5小时后在BC上D点相遇。已知两人上坡速度是4千米/小时,下坡速度是6千米/小时,在平路上速度是5千米/小时。则C至D是多少千米?
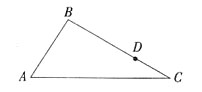
解:因李磊与韩梅梅在BC上D点处相遇,可以设李磊上坡用时x小时,则其下坡用时(2.5-x)小时,设韩梅梅走平路用时y小时,则其走上坡路用时(2.5-y)小时,则4B:BC:AC=4x:(25-6x-4y):5y=3:4:5。计算可得,x=1.5,y=2,则CD=4×(2.5-y)=2。
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | m | … |
10. 求这个二次函数的解析式。
解:设这个二次函数的解析式为y=a(x+1)(x-3)
∵点(0,-3)在函数图象上,
∴-3=a(0+1)(0-3)。
解得a=1。
∴这个二次函数的解析式为y=(x+1)(x-3)。
11. 求角B的大小;
解:由m∥n,得bcosC=(2a-c)cosB,bcosC+ccosB=2acosB,由正弦定理,sinBcosC+sinCcosB=2sinAcosB,sin(B+C)=2sinAcosB,
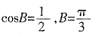
。
12. 设
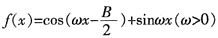
,且f(x)的最小正周期为π,求f(x)在区间
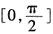
上的最大值和最小值。
解:由题知
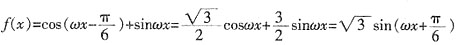
,由已知得
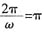
,ω=2,
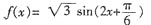
,当
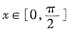
时,
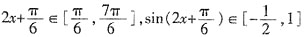
,所以,当
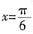
时,f(x)的最大值为
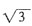
;当
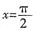
时,f(x)的最小值为
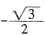
。
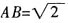 ,O为对角线A1C的中点。
,O为对角线A1C的中点。13. 求OD与底面ABCD所成的角的大小;
解:连接AC、BD交于点E,由AA
1=AD=1,
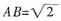
,则
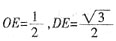
,故
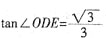
,即
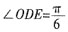
,故OD与底面所成的角为

。
14. P为AB上一动点,当P在何处时,平面PO⊥上平面A
1CD?并证明你的结论。
解:由AA
1=AD=1,
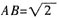
,则
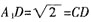
,又O为A
1C的中点,则OD⊥A
1C,于是当P为AB的中点时,
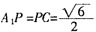
,从而OP⊥A
1C,故A
1C⊥平面POD。又
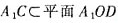
,则平面POD⊥平面A
1OD。
15. 已知函数f(x)=ax
3+bx
2-3x在x=+1处取得极值,讨论f(1)和(-1)是函数f(x)的极大值还是极小值。
解:f'(x)=3ax
2+2bx-3
由f(x)在±1处取得极值,故f'(1)=f'(-1)=0,
易得a=1,b=0。
| x
|
(-∞,-1)
|
-1
|
(-1,1)
|
1
|
(1,+∞)
|
| f'(x)
|
+
|
0
|
-
|
0
|
+
|
| f(x)
|
↗
|
极大值
|
↘
|
极小值
|
↗
|
故易得f(-1)是函数f(x)的极大值,f(1)是函数f(x)的极小值。
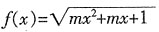 的定义域为R,则实数m的取值范围是______。
的定义域为R,则实数m的取值范围是______。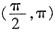 上为减函数的是______。
上为减函数的是______。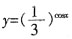
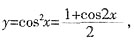 T=π,但在区间
T=π,但在区间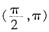 上为增函数。
上为增函数。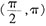 上为减函数。
上为减函数。
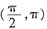 区间上为减函数,函数
区间上为减函数,函数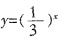 为减函数。因此
为减函数。因此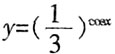 在
在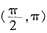 区间上为增函数。
区间上为增函数。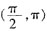 上为增函数。
上为增函数。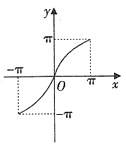
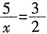 ,那么x的值是______。
,那么x的值是______。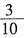
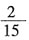
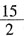
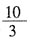
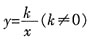 的图象过点(2,-2),则此函数的图象在直角坐标系中的______。
的图象过点(2,-2),则此函数的图象在直角坐标系中的______。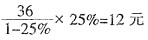 。另一件赚了25%,赚了
。另一件赚了25%,赚了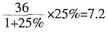 元。故总计亏了4.8元。
元。故总计亏了4.8元。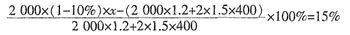
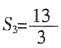 。
。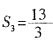 得
得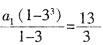 ,解得
,解得 ,所以
,所以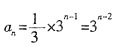 。
。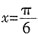 处取得最大值,且最大值为a3,求函数f(x)的解析式。
处取得最大值,且最大值为a3,求函数f(x)的解析式。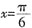 时f(x)取得最大值,所以
时f(x)取得最大值,所以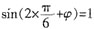 ;又0<φ<π,故
;又0<φ<π,故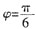 。所以函数f(x)的解析式为
。所以函数f(x)的解析式为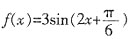 。
。

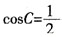 ,DE=6,求⊙O的直径。
,DE=6,求⊙O的直径。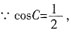
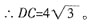
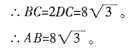
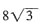 。
。
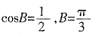 。
。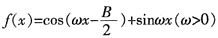 ,且f(x)的最小正周期为π,求f(x)在区间
,且f(x)的最小正周期为π,求f(x)在区间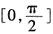 上的最大值和最小值。
上的最大值和最小值。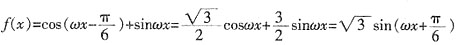 ,由已知得
,由已知得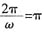 ,ω=2,
,ω=2,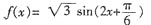 ,当
,当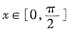 时,
时,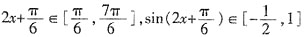 ,所以,当
,所以,当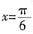 时,f(x)的最大值为
时,f(x)的最大值为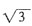 ;当
;当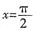 时,f(x)的最小值为
时,f(x)的最小值为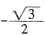 。
。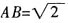 ,O为对角线A1C的中点。
,O为对角线A1C的中点。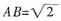 ,则
,则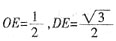 ,故
,故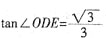 ,即
,即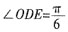 ,故OD与底面所成的角为
,故OD与底面所成的角为 。
。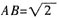 ,则
,则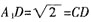 ,又O为A1C的中点,则OD⊥A1C,于是当P为AB的中点时,
,又O为A1C的中点,则OD⊥A1C,于是当P为AB的中点时,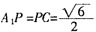 ,从而OP⊥A1C,故A1C⊥平面POD。又
,从而OP⊥A1C,故A1C⊥平面POD。又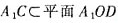 ,则平面POD⊥平面A1OD。
,则平面POD⊥平面A1OD。