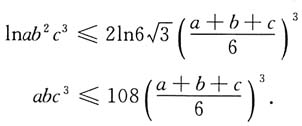解答题1.
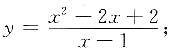
[解]
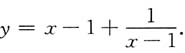
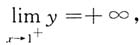
垂直渐近线为x=1.
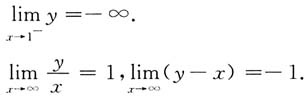
斜渐近线为y=x-1.
2. y=(1+x
2)e
-x2.
y=(1+x
2)e
-x2为偶函数,所以只须考虑x>0情况.
y'=2xe
-x2-2x(1+x
2)e
-x2=-2x
3e
-x2.
x>0时,y'<0,y递减,y(0)=1,
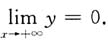
y"=-6x
2e
-x2+4x
4 e
-x2=(4x
4-6x
2)e
-x2.
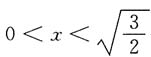
时,函数是凸的,
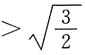
时,函数是凹的.
3. 设f,g为连续可微函数,u=f(x,xy),v=g(x+xy),求
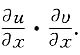
[解]
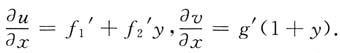
所以
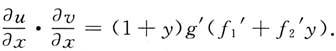
4. 设
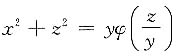
,其中φ为可微函数,求
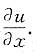
[解] 原式两边对y求导,x是y的函数,得
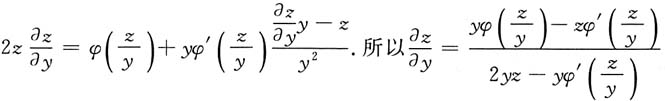
5. 设u=f(x,y,z),又y=φ(x,t),t=ψ(x,z),求
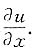
[解]
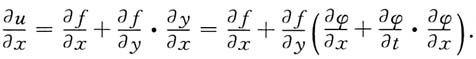
8. 设z=f(e
xsiny,x
2+y
2),其中f具有二阶连续偏导数,求
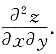
[解]
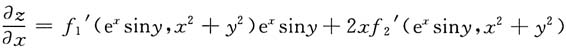
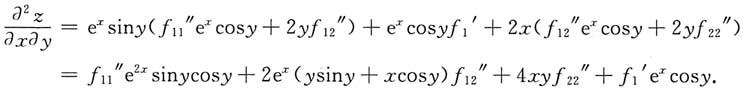
10. 已知z=f(xlny,x-y),求
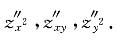
[解]
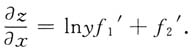
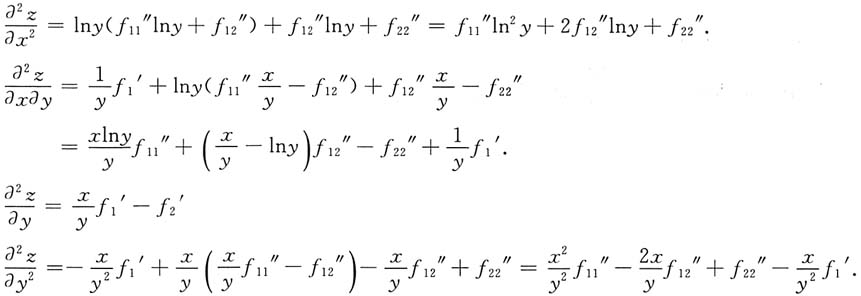
11. 设y=y(x),z=z(x),由
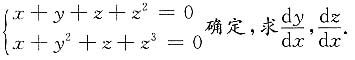
[解] 以上两式对x求导,得

由克莱姆法则解得
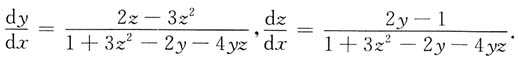
13. 设z=f[x
2-y,φ(xy)],其中f(u,v)具有二阶连续偏导数,φ(u)二阶可导,求
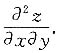
[解]
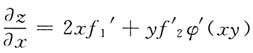
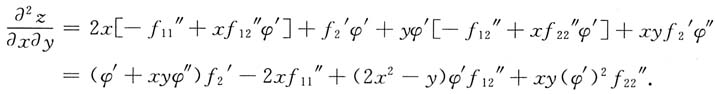
14. 已知z=z(u),且
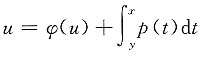
,其中z(u)可微,φ'(u)连续,且φ(u)≠1,p(t)连续,试求
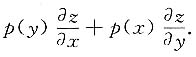
[解]
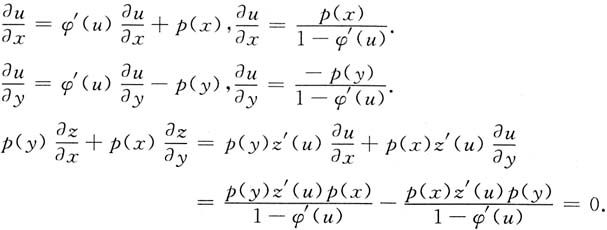
15. 设F(x,y(x),z(x))=P(x,y(x))+Q(x,y(x))z(x),其中出现的函数都是连续可微的,试计算
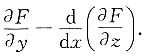
16. 设z=u(x,y)e
ax+y,
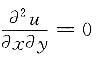
,试确定常数a,使
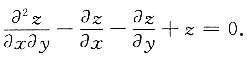
[解]
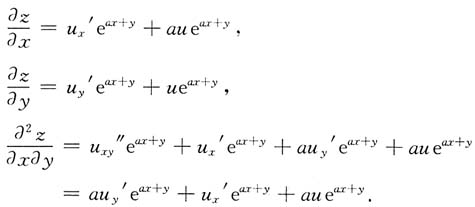
所以
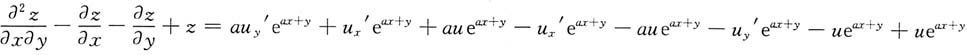
=au
y'e
ax+y-u
y'e
ax+y=0.
于是a=1.
17. 若

满足
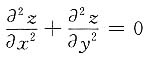
,其中f(u)有连续的二阶导数,求z.
[解]
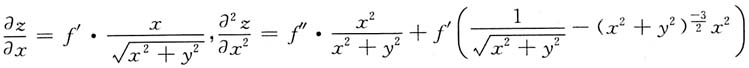
同理可得
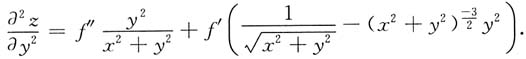
所以
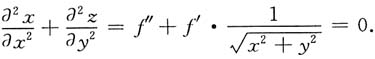
令
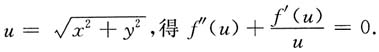
于是uf"(u)+f'(u)=0.(uf'(u))'=0
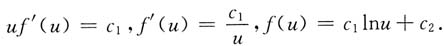
即
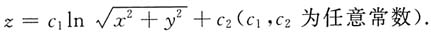
18. 试求函数z=x
2+y
2-xy+x+y在闭域D:x≤0,y≤0及x+y≥-3上的最大值与最小值.
[解]
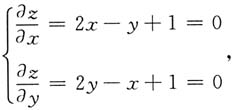
解得x=-1,y=-1,z(-1,-1)=-1.
当x=0时,x=y
2+y,-3≤y≤0.
最大值为z(0,-3)=9,最小值为
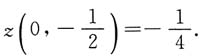
当y=0时,z=x
2+x,-3≤x≤0.
最大值为z(-3,0)=6.最小值为
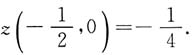
当x+y=-3时,z=3x
2+9x+6,-3≤x≤0.
当
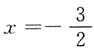
时z有最小值
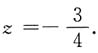
即

当x=0时z有最大值z=6.即z(0,-3)=6.
当x=-3时z有最大值z=6.即z(-3,0)=6.
综上所述:z(0,-3)=z(-3,0)=6为最大值,z(-1,-1)=-1为最小值.
19. 在椭球面
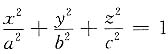
内作内接直角平行六面体,求其最大体积.
[解] 设直角平行六面体在第一象限的顶点为(x,y,z).
题目转化为求V=8xyz的最大值,其中x,y,z满足

令
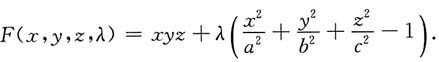

当x→a-,y→b-,z→c-任意一个成立时,都有Ⅴ→0.所以
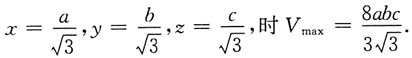
20. 求原点到曲面(x-y)
2-z
2=1的最短距离.
[解] 设曲面上达到最短距离的点为(x,y,z),则题目转化为求d
2=x
2+y
2+z
2的最小值,其中x,y,z满足(x-y)
2-z
2=1.令F(x,y,z,λ)=x
2+y
2+z
2+λ(x-y)
2-λz
2-λ
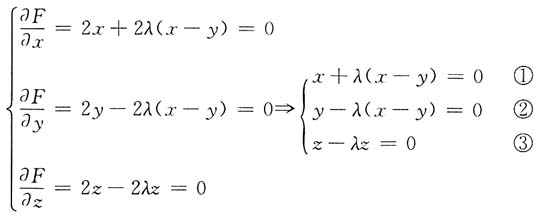
由③,若λ=1,
代入①,②得
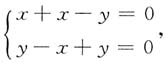
解得x=0,y=0.代入曲面方程(x-y)
2-z
2=1,得到z
2=-1,此时d不存在.
由③,若λ≠1,解得z=0,由①,②得到x=-y,代入曲面方程(x-y)
2-z
2=1,得到
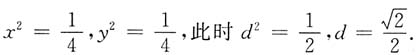
所以所求的最短距离为
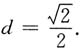
21. 当x>0,y>0,z>0时,求函数u=lnx+2lny+3lnz在球面x
2+y
2+z
2=6r
2上的最大值,并证明对任意的正实数a,b,c成立不等式
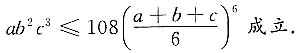
[解] 构造函数F(x,y,z,λ)=lnx+2lny+31nz-λ(x
2+y
2+z
2-6r
2).

因为在球面上当y
2+z
2趋于6r
2,x趋于0
+时,u趋于-∞.
所以当x=r,
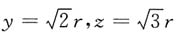
时,u达到最大值.
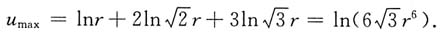
对于任意正实数a,b,c,令
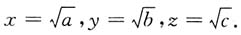
则
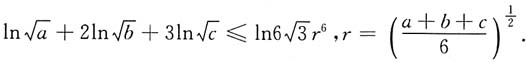
即