一、单项选择题本大题共10小题，每小题2分，共20分。4. 设随机变量X～N(-1，2
2)，
(x)为标准正态分布函数，则P{-1＜X≤2}=______。
A．
(2)-
(-1)
B．
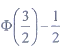
C．
D．
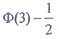
A B C D
8. 设总体X～N(μ，σ
2)，其中μ未知，X
1，X
2，X
3，X
4为来自该总体的样本，在μ的无偏估计
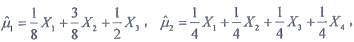
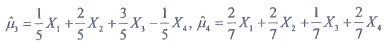
中，较有效的是______。
A．
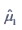
B．
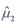
C．
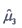
D．
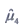
A B C D
10. 设X
1，X
2，.......，X
n，(n>1)为来自正态总体N(μ，σ
2)的样本，其中σ
2未知，
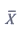
和S
2分别是样本均值和样本方差，对于检验假设H
0：μ=μ
0；H
1：≠μ
0，当显著性水平为a时H
0的拒绝域为______。
A．
B．
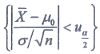
C．
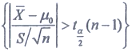
D．
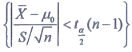
A B C D
二、填空题本大题共15小题，每小题2分，共30分。1. 设A，B为随机事件，且
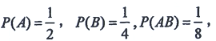
则P(AUB)=______.
2. 将一个白球和一个红球随机放入甲、乙两个盒中，事件A表示“两个球都放入甲盒中”，则P(A)=______.
3. 设P(A)=0.7，P(A-B)=0.3，则
=______.
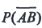
4. 设随机变量X服从区间[1，5]上的均匀分布，则P{2＜X≤3}=______.
5. 设随机变量X服从参数为3的泊松分布，则P{X＜2}=______.
6. 设二维随机变量(X，Y)的分布律为
则P{X=Y}=______.
7. 设随机变量X，Y，Z相互独立，且X～N(0，1)，Y～N(-1，1)，Z～N(1，1)，则X+Y+Z～______.
8. 设随机变量X与Y相互独立，X和Y的概率密度分别为
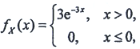
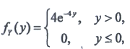
则P{0≤X≤1，0≤Y≤2}=______.
9. 设随机变量X～B(6，0，2)，则D(-2X+3)=______.
10. 设总体X～N(10，2
2)，从该总体随机抽取容量为9的样本，
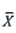
为样本均值，φ(x)为标准正态分布函数，且φ(3)=0.9987，则
=______.
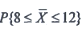
11. 设总体X～N(μ，σ
2)，X
1，X
2，.......，X
n为来自X的样本，
为样本均值，s
2为样本方差，则
______.
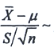
12. 设X
1，X
2，X
3，X
4为来自总体X的样本，且X～N(μ，3
2)，
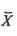
为样本均值，则
=______.
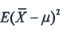
13. 设X
1，X
2，.......，X
9为来自正态总体N(0，1的样本，则
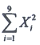
服从的分布是______.
14. 设X
1，X
2，.......，X
n为来自正态总体
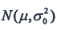
的样本，
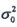
已知，s
2为样本方差，则E(S
2)=______.
15. 设某个检验假设的拒绝域为W，当原假设H
0成立时，样本(X
1，X
2，.......，X
n)∈W的概率为0.1，则犯第一类错误的概率为______.
五、应用题10分。1. 设某产品长度(单位：mm)服从正态分布N(μ，σ
2)，现随机抽取该产品36件，测其长度并算得样本均值
=2050，样本标准差s=250，可否认为这批产品的平均长度为2000(mm)?(附：a=0.1，t
0.05(35)=1.6896)
假设H
0：μ=μ
0；H
1：μ≠μ
0，
取检验统计量
，当
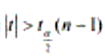
，拒绝H
0；
由题意可知
=2050，s=250，n=36，μ
0=2000，
a=0.1，t
0.05(35)=1.6896，计算可得t=1.2，
由于|t|＜t
0.05(35)，故接受H
0，
即可以认为这批产品的平均长度为2000mm.
，
，则P(AB)=______。
则常数c=______。
则P{X=-2|Y=1}=______。
为样本均值，则θ的矩估计是______。
，P(B)=0.4，
.求：
.
Y服从区间[0，4]上的均匀分布.
深色：已答题 浅色：未答题