一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)3. 当x→0时,下面无穷小量中与x等价的无穷小量是______
- A.5x
- B.ln(1+x3)
- C.sinx
- D.x+sinx
A B C D
C
[考点] 本题主要考查的知识点是无穷小量的比较.
[解析] 选项A中,
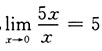
;选项B中

;选项C中

;选项D中
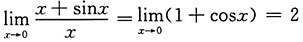
.
5. 如果级数
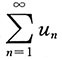
收敛,且s
n=u
1+u
2+…+u
n,则数列s
n______
A B C D
C
[考点] 本题主要考查的知识点是级数的前n项和数列敛散性的判断.
[解析] 由级数收敛的定义知,级数

收敛于s,当级数收敛时,其任意的前n项和s
n的极限存在,且都等于s.故数列s
n收敛.
二、填空题1. 设函数y=f(x)的定义域为[0,1],则函数f(sinx)的定义域为______.
[2kπ,(2k+1)π]
[考点] 本题主要考查的知识点是复合函数定义域的求解.
[解析] 函数f(x)的定义域为[0,1],则在f(sinx)中有0≤sinx≤1,
故有2kπ≤x≤(2k+1)π.
2. 设f(x)在x=1处连续,且
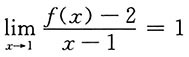
,则f(1)=______.
3. 在函数
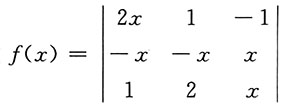
中,x
3的系数是______.
4. 设y=f(x)在x
0处可导,且在点x
0处取得极小值,则曲线y=f(x)在点(x
0,f(x
0))处的切线方程为______.
y=f(x0)
[考点] 本题主要考查的知识点是曲线在某点处的切线方程.
[解析] 由题意可知,切线方程可表示成
y-f(x0)=f'(x0)(x-x0),
但由于y=f(x)在x0处可导,且在点x0处取得最小值.
∴f'(x0)=0,
∴切线方程为y=f(x0).
5. 函数y=x+2cosx在区间
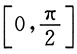
上最大值为______.
[考点] 本题主要考查的知识点是函数的最值.
[解析] y=x+2cosx,
∴y'=1-2sinx=0,
则
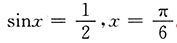
.
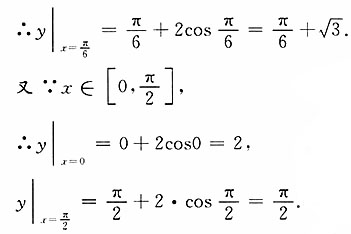
∴最大值为

.
6. 设
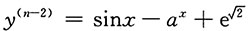
,(a>0,a≠1)则y
(n)=______.
7. 双曲线

在点(1,1)处的切线方程为______.
y-1=-(x-1)
[考点] 本题主要考查的知识点是曲线的切线方程.
[解析]
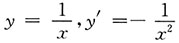
,x=1,y'=-1.所以在点(1,1)处的切线方程为y-1=-(x-1).
8. 定积分
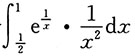
=______.
三、计算题1. 已知矩阵A满足关系式A
2+2A-3E=O,求(A+4E)
-1.
解:设法分解出因子A+4E,
由A
2+2A-3E=O,
有(A+4E)(A-2E)+8E-3E=O,
即(A+4E)(A-2E)=-5E,
即
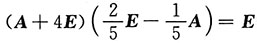
,
得
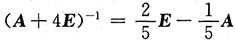
.
[考点] 本题主要考查的知识点是逆矩阵的求法.
2. 函数f(x)=ax
3-4ax
2+b(a>0)在[-1,2]上的最大值为3,最小值为-13,试确定a,b的值.
解:
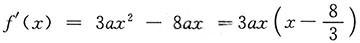
,驻点为x=0,
| x
|
-1
|
(-1,0)
|
0
|
(0,2)
|
2
|
| f'(x)
|
|
+
|
0
|
-
|
|
| f(x)
|
-5a+b
|
↗
|
b
|
↘
|
-8a+b
|
因为a>0,所以最大值f(0)=b=3,最小值f(2)=-8a+b=-13,
即a=2,b=3.
[考点] 本题主要考查的知识点是函数在某区间上的最值.
3. 判断级数
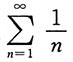
的敛散性.
解:由于级数
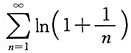
的前n项和s
n为
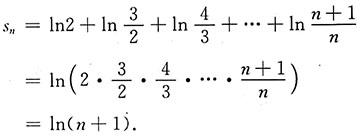
由函数y=ln(x+1)的图像知极限
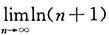
不存在,所以极限
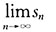
不存在,故级数发散.而
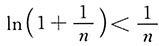
,故级数
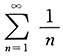
也发散.
[考点] 本题主要考查的知识点是级数敛散性的判断.
4. 设f(x)=(x-1)φ(x),且φ(x)在x=1处连续,试证明f(x)在点x=1处可导.
解:

(因为φ(x)在x=1处连续,所以
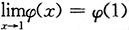
.)所以f(x)在x=1处可导.
[考点] 本题主要考查的知识点是函数在某点处的可导性.
5. 设f(x)在x=2处连续,且f(2)=3,求
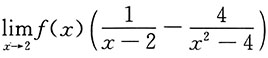
.
解:由于f(x)在x=2处连续,且f(2)=3,可知必有
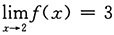
,从而
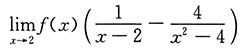
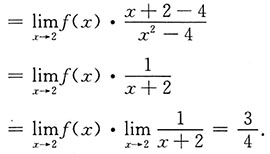
[考点] 本题主要考查的知识点是极限的运算.
6. 利用函数的单调性证明:当x>0时,
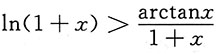
.
解:本题即需证x>0时,
(1+x)ln(1+x)>arctanx,
令f(x)=(1+x)ln(1+x)-arctanx,则
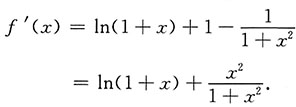
显然x>0时,有f'(x)>0.
又因为f(x)在[0,+∞)上连续,所以f(x)在[0,+∞)上单调增加.
于是当x>0时,有f(x)>f(0)=0,
即(1+x)ln(1+x)-arctanx>0.
也即
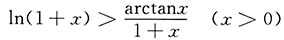
成立.
[考点] 本题主要考查的知识点是函数单调性的应用.
7. 利用一阶微分形式不变性及微分运算法则,求y=e
x2sin3x的微分.
解:

[考点] 本题主要考查的知识点是函数的微分.
四、综合题1. 求椭圆
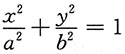
与坐标轴所围面积,及椭圆曲线分别绕x轴,y轴旋转一周所成的体积.
解:由对称性知,所求面积应是第一象限部分面积的4倍,即
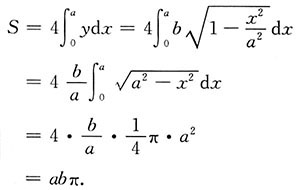
绕x轴旋转一周所成旋转体体积,由对称性,得
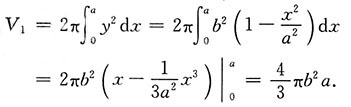
同理绕y轴旋转一周所成旋转体积为
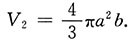
[考点] 本题主要考查的知识点是由曲线所围成的平面图形绕x轴、y轴旋转后的旋转体体积.
2. 求函数在给定区间上的最值:
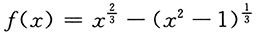
,x∈[-2,2].
解:

.
驻点:
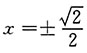
,不可导点:x=0,x=±1,区间
端点:x=±2.
由于f(x)为偶函数,因此只需计算:

比较可得,最大值为
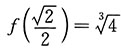
,最小值为
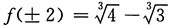
.
[考点] 本题主要考查的知识点是函数在某区间上的最值.