一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)2. 设f(x)的一个原函数是x
2,则∫xf(1-x
2)dx=______
A.
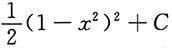
B.
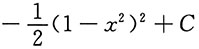
C.(1-x
2)
2+C
D.-2(1-x
2)
2+C
A B C D
B
[考点] 本题主要考查的知识点是原函数的应用.
[解析] 由f(x)的原函数是x
2,

5. 设
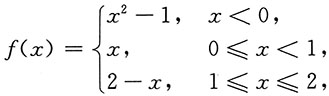
则f(x)在______
- A.x=0,x=1处都间断
- B.x=0处间断,x=1处连续
- C.x=0处连续,x=1处间断
- D.x=0,x=1处都连续
A B C D
B
[考点] 本题主要考查的知识点是函数在某点处间断、连续的判断.
[解析]
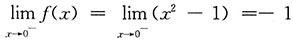
,
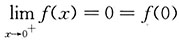
,f(x)在x=0处左右极限存在但不相等,在x=0处间断.
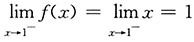
,
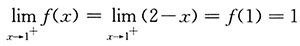
,f(x)在x=1处左右极限存在且都等于f(1),连续.
四、综合题1. 午夜零时,甲船位于乙船正东75公里处,且以时速12公里朝西航行,而乙船以时速6公里向北航行,问何时两船相距最近.
解:设经过x小时后两船相距S公里.
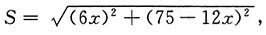
为便于求导,令y=(6x)
2+(75-12x)
2,
y'=360x-1800,
驻点x=5.
故早晨5点时两船相距最近.
[考点] 本题主要考查的知识点是一阶导数的实际应用.
2. 一曲线从原点经过点(1,1)伸向第一象限,曲线从O(0,0)到P(x,y)的一段弧与z轴及过P点平行y轴的直线所围面积等于以OP为对角线且边分别平行坐标轴的矩形面积的
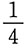
.求该曲线方程.
解:
依题意可得
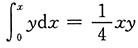
,
两端对x求导
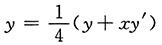
,
即xy'=3y,
变量分离
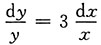
,
所以lny=3lnx+lnC(C>0).
即y=Cx
3.
因为x=1,y=1,所以C=1.
所求曲线为y=x
3(x>0).
[考点] 本题主要考查的知识点是定积分的几何意义及微分方程的求解.