一、单项选择题(在每小题列出的四个备选项中只有一个是符合题目要求的。)5.
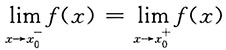
是函数f(x)在点x=x
0处连续的______
- A.必要条件
- B.充分条件
- C.充分必要条件
- D.既非充分又非必要条件
A B C D
A
[考点] 本题主要考查的知识点是函数在某点处连续的充分必要条件.
[解析] 函数f(x)在点x
0处连续必须同时满足的三个条件是:f(x)在x
0点有定义,

存在,f(x
0)与

相等.因此有函数f(x)在点x
0处连续可推出:
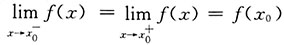
.故
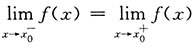
是函.数f(x)在点x=x
0处连续的必要条件.
又因为函数f(x)在点x
0处无定义时,f(x)在点x
0处间断,故有
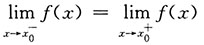
不能推出f(x)在点x
0处连续,因此不是充分条件.
二、填空题1. 若函数y=x
2+kx+1在点x=-1处取极小值,则k=______.
2
[考点] 本题主要考查的知识点是函数的极值.
[解析] 函数在x=-1处取极小值.
则y'=2x+k=0.
∴2×(-1)+k=0.
∴k=2.
2. 曲线

上点______处的切线平行于直线y=3x+2.
(4,8)
[考点] 本题主要考查的知识点是函数导数的几何意义.
[解析]
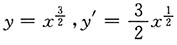
,令y'=3.得x=4,则y=8.故曲线上点(4,8)处的切线平行于直线y=3x+2.
3. 若函数y=f(x)在x=x
0处取得极值,则f'(x
0)______.
=0或不存在
[考点] 本题主要考查的知识点是函数取得极值的条件.
[解析] 函数f(x)在x=x0处取得极值的必要条件是f'(x0)=0或f(x)在x=x0处不可导,即f'(x0)不存在.
4. 设
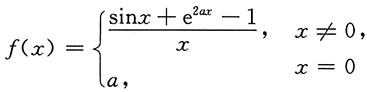
在(-∞,+∞)内连续,则a=______.
-1
[考点] 本题主要考查的知识点是函数连续的定义.
[解析] f(x)在(-∞,+∞)内连续,则f(x)在x=0处连续,则有
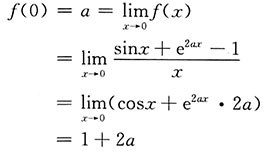
所以a=-1.
5. 若在(a,b)内的曲线弧y=f(x)是凸的,则曲线必位于其上每一点处切线的______方.
6. 设函数g(x)=2
x,f(x)=x
2,则f[g(x)]=______.
22x
[考点] 本题主要考查的知识点是复合函数的运算.
[解析] f(x)=x2,f[g(x)]=[g(x)]2=(2x)2=22x.
7. 设函数y=lg(kx
2-3x+2k)的定义域为一切实数,则k的取值范围是______.
[考点] 本题主要考查的知识点是对数函数定义域的取值范围.
[解析] 因为函数y的定义域为一切实数,则kx
2-3x+2k>0对一切x都成立.所以k>0且有Δ=9-8k
2<0恒成立,即
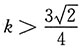
.
8. 要使y=arcsinau(a>0),u=2+x
2,能构成复合函数,则a的取值范围为______.
[考点] 本题主要考查的知识点是复合函数的定义域.
[解析] 由u=2+x
2可知u∈[2,+∞).
由y=arcsinau知au∈[-1,1].
又∵a>0,
∴au∈[0,1],
∴
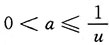
.
又∵u≥2,∴
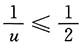
.
∴
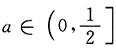
.
三、计算题1. 设矩阵
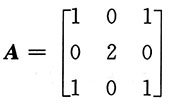
,矩阵X满足AX+E=A
2+X,试求矩阵X.
解:由题设知AX+E=A
2+X,即
(A-E)X=A
2-E=(A-E)(A+E).
因为
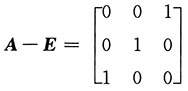
是可逆矩阵,所以

[考点] 本题主要考查的知识点是矩阵的运算.
2. 利用函数的单调性证明:方程sinx=x有且只有一个实根.
解:显然有一根x=0.设f(x)=sinx-x,f'(x)=cosx-1≤0.所以f(x)单调递减,则f(x)至多有一个零点ξ.使得f(x)=0.即sinξ=ξ.因此sinx=x有且只有一个实根x=0.
[考点] 本题主要考查的知识点是方程实根的求法.
3. 求定积分:
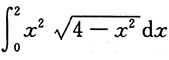
.
解:作三角代换,见下图
令x=2sint,
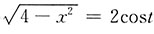
.
dx=2costdt,当x=0时,t=0;
当x=2时,
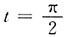
.
所以
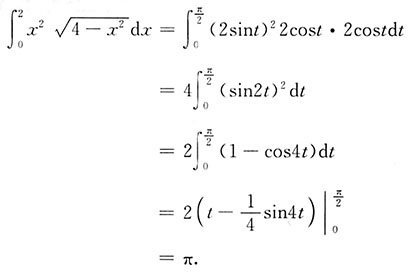
[考点] 本题主要考查的知识点是定积分的计算.
4. 求曲线
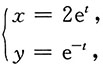
在t=0处的切线方程和法线方程.
解:
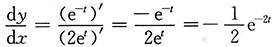
,
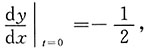
当t=0时,x=2,y=1.
故所求切线方程为
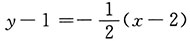
,
即
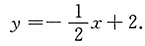
法线方程为y-1=2(x-2),
即y=2x-3.
[考点] 本题主要考查的知识点是曲线在某点处的切线和法线方程.
5. 判断级数

的敛散性.
解:由于此级数的前n项和s
n为
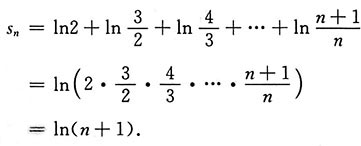
由函数y=ln(x+1)的图像知极限
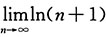
不存在,所以极限
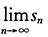
不存在,故级数发散.
[考点] 本题主要考查的知识点是级数敛散性的判断.
6. 计算不定积分:
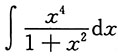
.
解:
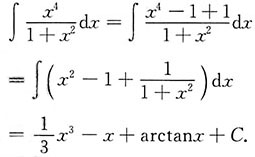
[考点] 本题主要考查的知识点是不定积分的计算.
7. 设函数
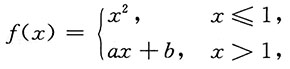
试确定a,b的值,使f(x)在x=1处可导.
解:设f(x)在x=1处可导,则f(x)在x=1处一定连续.又x=1是分段点,则必有左导数等于右导数,既右连续又左连续.
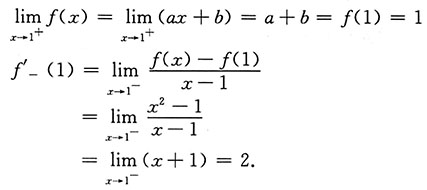

故a=2,b=-1.
即a=2,b=-1时,f(x)在x=1处可导.
[考点] 本题主要考查的知识点是函数在某点处可导的条件.