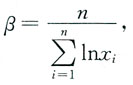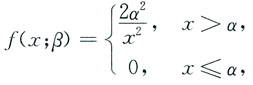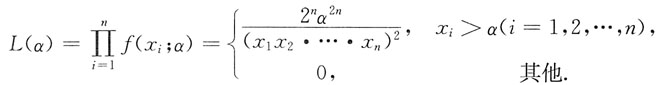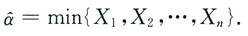一、选择题(下列每题给出的四个选项中,只有一个选项是符合题目要求的.)
1. 设f(x)在点x
0处连续,且
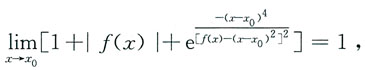
则______
- A.x0不是f(x)的驻点
- B.x0是f(x)的驻点,但不是极值点
- C.x0是f(x)的极大值点
- D.x0是f(x)的极小值点
A B C D
D
[解析] 由已知极限可推得
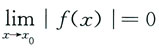
及
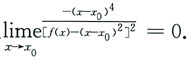
由于f(x)在x
0处连续,所以由
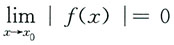
知f(x
0)=0.又
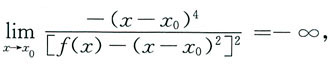
可知
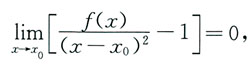
故
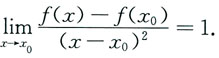
从而知存在δ>0,在x
0的某空心邻域内f(x)-f(x
0)>0,即x
0是f(x)的极小值点,故选D.
本题考查的知识点是:极限的应用及对函数极值的理解.
2. 设f(x,y)为连续函数,则使
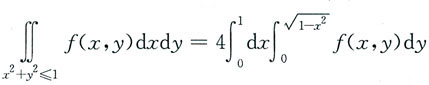
成立的充分条件是______
- A.f(-x,-y)=-f(x,y)且f(-x,y)=f(x,y)
- B.f(-x,-y)=f(x,y)
- C.f(-x,-y)=-f(x,y)
- D.f(-x,y)=f(x,y)且f(x,-y)=f(x,y)
A B C D
D
[解析] 若f(x,y)关于x为偶函数,关于y也是偶函数,记D
1为x
2+y
2≤1的第一象限部分,则有
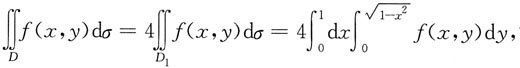
故选D.
本题考查的知识点是:二重积分的计算.
3. 设
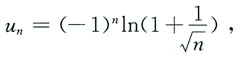
则级数______
A.
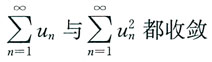
B.
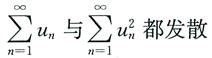
C.
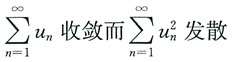
D.

A B C D
C
[解析] 由于{u
n}为交错级数,所以根据莱布尼茨定理知,
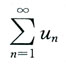
收敛,而
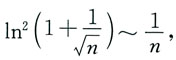
所以
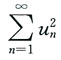
发散,故选C.
本题考查的知识点是:莱布尼茨公式及等价无穷小的应用.
4. 设
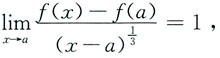
则函数f(x)在点a处必然______
A B C D
D
[解析] 注意到
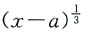
与x-a同号,因此

说明:存在δ>0,使得a<x<a+δ时,f(x)>f(a);同时,a-δ<x<a时,f(x)<f(a),故f(a)不是极值点,所以A,B均不正确.又因为
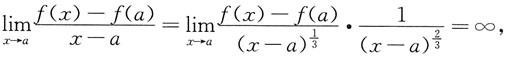
所以f(x)在a点不可导,C不正确,故选D.
本题考查的知识点是:通过极限的定义来说明函数在某点处是否可导.
5. 设A是三阶矩阵,|A|=3,A
2+2A=0,2A
2+A=0,则A
*的全部特征值是______
A.
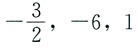
B.-2,-1,3
C.2,1,3
D.
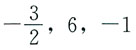
A B C D
A
[解析] A
2+2A=A(A+2E)=0,因|A|=3,A可逆,故|A+2E|=0,A有特征值λ
1=-2,同理A+2A
2=A(E+2A)=0,|2A+E|=0,A有特征值
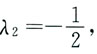
且有λ
1λ
2λ
3=|A|=3,因此,λ
3=3.又有Aξ
i=λ
iξ
i,i=1,2,3,在其两边同乘A
*得
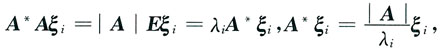
则A
*有特征值
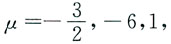
因此选A.
本题考查的知识点是:求矩阵及其伴随矩阵的特征值.
7. 设随机变量X与Y相互独立,且均服从正态分布N(0,1),则______
A.
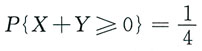
B.
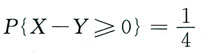
C.
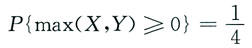
D.

A B C D
D
[解析] 若记A={X≥0},B={Y≥0},则A与B相互独立,且
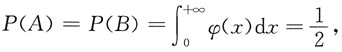
故
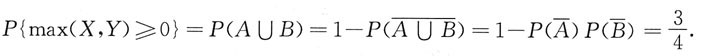
而

因此,选D.
本题考查的知识点是:随机变量组合的概率计算.
8. 对两个仪器进行独立试验,已知其中一个仪器发生故障的概率为p
1,另一个发生故障的概率为p
2,则发生故障的仪器数的数学期望为______
- A.p1p2
- B.p1(1-p2)+p2(1-p1)
- C.p1+(1-p2)
- D.p1+p2
A B C D
D
[解析] 设X
i表示第i台仪器发生故障(i=1,2),则其分布列为
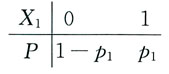
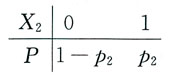
仪器发生故障的台数X=X
1+X
2的分布列为
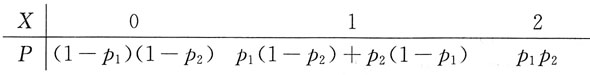
于是E(X)=E(X
1+X
2)=E(X
1)+E(X
2)=p
1+p
2 或E(X)=1×[p
1(1-p
2)+p
2(1-p
1)]+2×p
1p
2=p
1+p
2.
故选D.
本题考查的知识点是:数学期望的应用.
二、填空题(每小题4分,共24分.)
1.
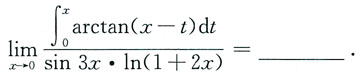
[解析] 因为

于是
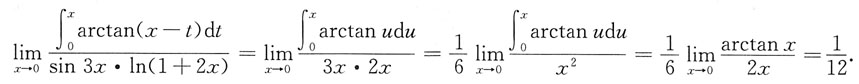
本题考查洛必达法则求极限.
2. 设f(x,y)连续,且
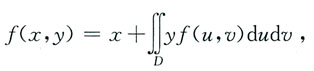
其中D是由
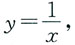
x=1,y=2所围区域,则f(x,y)=______.
[解析] 令

则A为常数,此时f(x,y)=x+Ay.等式两边同时取二重积分得
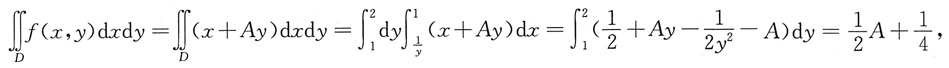
即
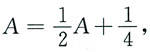
得
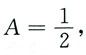
故
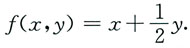
本题考查二重积分的基本计算.
3. 设f(x)有一个原函数为1+sin
2x,则
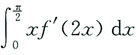
=______.
0
[解析]
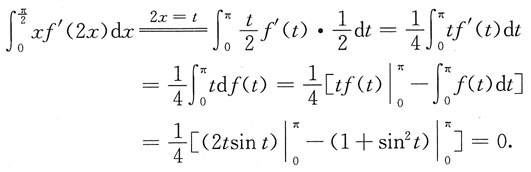
本题考查分部积分法计算定积分.
4. 微分方程y'+ytanx=cosx的通解为______.
(x+C)cosx
[解析] 此为一阶线性微分方程,代公式得通解.
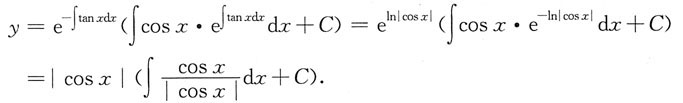
当cosx>0时,
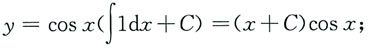
当cosx<0时,
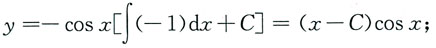
由于C为任意常数,故两式可以统一写为y=(x+C)cosx.
本题考查一阶线性微分方程的通解.
5. 设A,B为三阶矩阵,且A的三个特征值为1,2,3,则矩阵
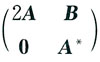
的特征值为______.
2,4,6,6,3,2
[解析]
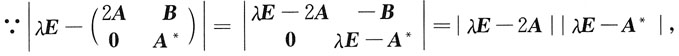
∴只需分别求出2A,A
*的特征值即可.设λ为A的特征值,则有Ax=λx,x≠0,于是2Ax=2λx,
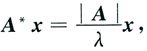
即2A,A
*分别有特征值2λ,
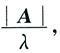
由题设λ
1=1,λ
2=2,λ
3=3,且|A|=λ
1λ
2λ
3=6,故所求特征值为2,4,6,6,3,2.
本题考查特征值的求法.
6. 已知随机变量X服从自由度为n的t分布,则随机变量X
2服从的分布是______.
F(1,n)
[解析] 因为X~t(n),令
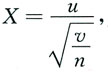
其中u~N(0,1),v~χ
2(n),且u,v相互独立,于是
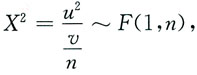
其中u
2~χ
2(1).
三、解答题(共94分.解答应写出文字说明、证明过程或演算步骤.)
1. 求极限
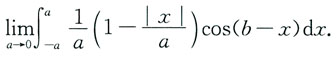
2. 设u=u(x,y)满足方程
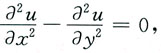
且u(x,2x)=x,u
x(x,2x)=x
2,求u
xx(x,2x),u
xy(x,2x),u
yy(x,2x).
将u(x,2x)=x两边对x求导,得u
x(x,2x)+u
y(x,2x)·2=1.由条件u
x(x,2x)=x
2推得u
y(x,2x)·2=1-x
2,再将得到的u
x与u
y两个表达式对x求导,得u
xx(x,2x)+u
xy(x,2x)·2=2x及u
yx(x,2x)·2+u
yy(x,2x)·4=-2x.再代入条件u
xx(x,2x)-u
yy(x,2x)=0,解得
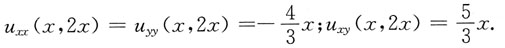
3. 设L是不经过点(2,0),(-2,0)的分段光滑的简单闭曲线,试就L的不同情形计算曲线积分:

L取正向.
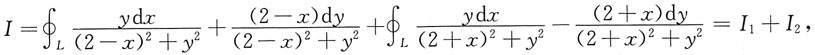
不难验证:对I
1有
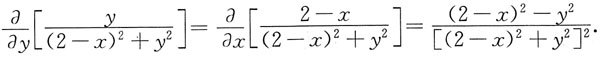
对I
2有
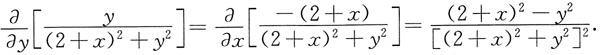
即它们都分别满足
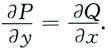
以下就L的情况讨论:
(1)当点(2,0),(-2,0)均在闭曲线L所围区域的外部时,I
1=0=I
2,从而I=0.
(2)当点(2,0),(-2,0)同在L所围区域的内部时,则分别作以这两个点为圆心,以ε
1,ε
2为半径的圆C
1,C
2使它们也都在区域内部,于是
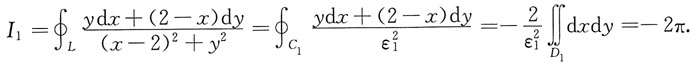
(其中C
1取正向,D
1是C
1所围区域)
同理,I
2=-2π,所以I=-4π.
(3)当点(2,0),(-2,0)有一个在外部一个在内部时,综合(1),(2)得I=-2π.
4. 设f(x)在x=0的某邻域内具有二阶连续导数,并设f(x)为偶函数,且f(0)=1,试证明级数
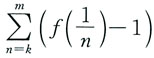
绝对收敛,其中k为足够大的正数.
由二阶导数连续及f(x)为偶函数,有f'(0)=0.由泰勒公式
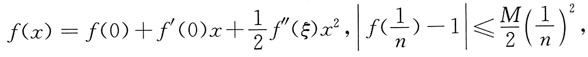
其中M=max{f"(x)}.
由比较审敛法及p=2时,p级数
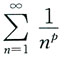
收敛,得原级数绝对收敛.
5. 设曲线y=f(x),其中y=f(x)是可导函数,且f(x)>0.已知曲线y=f(x)与直线y=0,x=1及x=t(t>1)所围成的曲边梯形,绕x轴旋转一周所得的立体体积值是该曲边梯形面积值的πt倍,求该曲线方程.
旋转体的体积为:
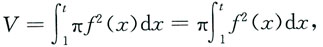
曲边梯形的面积为:
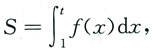
则由题设可知
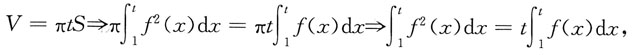
两边对t求导可得
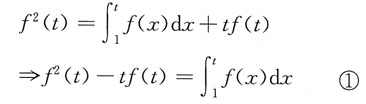
再次求导可得2f(t)f'(t)-f(t)-tf'(t)=f(t),
化简可得
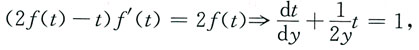
解之得

在①式中令t=1,则f
2(1)-f(1)=0,
∵f(t)>0,
∴f(1)=1,
代入
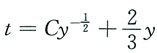
得
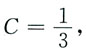

所以该曲线方程为:
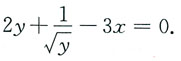
6. 设向量α
1(1,-1,2,-1)
T,α
2=(-3,4,-1,2)
T,α
3=(4,-5,3,-3)
T,α
4=(-1,λ,3,0)
T,β=(0,k,5,-1)
T.
试问λ,k取何值时,β不能由α
1,α
2,α
3,α
4线性表出?λ,k取何值时,β可由α
1,α
2,α
3,α
4线性表出?并写出线性表达式.
本题相当于讨论线件方程组
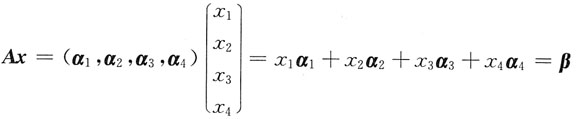
何时有解,无解.
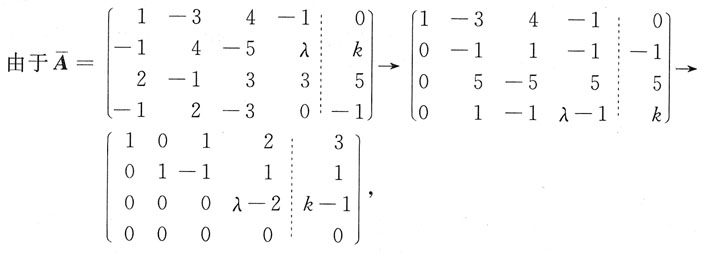
当k≠1,λ=2时,β不能由α
1,α
2,α
3,α
4线性表出;当k=1,λ=2时,β可由α
1,α
2,α
3,α
4线性表出,且表示法不唯一.

所以β=(3-k
1-2k
2)α
1+(1+k
1-k
2)α
2+k
1α
3+k
2α
4(其中k
1,k
2为任意常数).
当λ≠2,k为任意值时,β可由α
1,α
2,α
3,α
4线性表出,且表示法不唯一.

所以
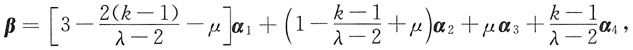
其中λ≠2,k,μ为任意常数.
7. 设A为r阶方阵,B为r×n矩阵,r(B)=r,且AB=0,证明:A=0.
因为r(B)=r,所以矩阵B有r个线性无关的列向量,故经过初等列变换将B化成
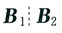
的形式,其中B
1是r×r矩阵,B
2=0,r(B
1)=r,即存在可逆阵Q,使得BQ=B
1B
2.
由于AB=0,所以
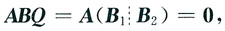
因而AB
1=0,两边同乘
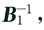
得A=0.
8. 设A为n阶正交阵,且A的特征值都大于零,证明:A
*=A
T.
由A的特征值都大于零知|A|>0.又A为正交阵,故|A|=1,从而A*=|A|A-1=A-1=AT.
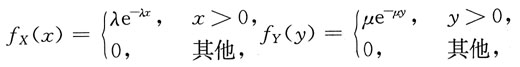
其中λ>0,μ>0是常数,引入随机变量9. 求条件概率密度f
X|Y(x|y);
由题设
y>0时,
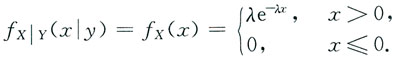
10. 求Z的分布律及分布函数.
由二元密度的概率意义,及题设X和Y独立且为指数分布,则
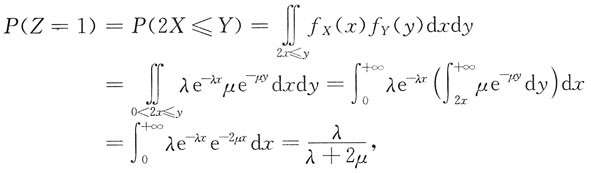
故
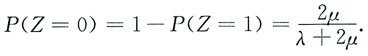
于是z的分布律为:
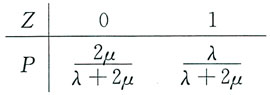
分布函数为:

11. 设随机变量X的分布函数为
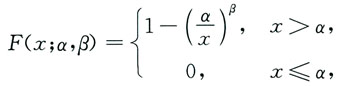
其中参数α>0,β>1.设X
1,X
2,…,X
n为来自总体X的简单随机样本.
(1)当α=1时,求未知参数β的矩估计量;
(2)当α=1时,求未知参数β的最大似然估计量;
(3)当β=2时,求未知参数α的最大似然估计量.
本题是一个常规题型.求连续型总体未知参数的矩估计和最大似然估计都须已知密度函数,从而先由分布函数求导得密度函数.
当a=1时,X的概率密度为
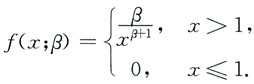
(1)由于
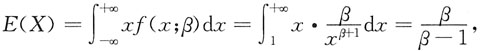
令
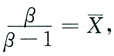
解得

所以,参数β的矩估计量为
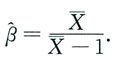
(2)对于总体X的样本值x
1,x
2,…,x
n,似然函数为

当x
i>1(i=1,2,…,n)时,L(β)>0,取对数得
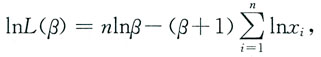
对β求导数,得
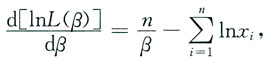
令
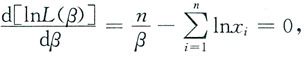
解得
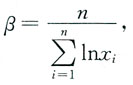
于是β的最大似然估计量为

(3)当β=2时,X的概率密度为
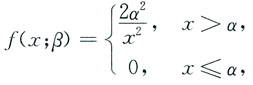
对于总体X的样本值x
1,x
2,…,x
n,似然函数为
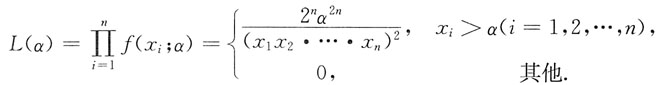
当x
i>a(i=1,2,…,n)时,α越大,L(α)越大,即α的似然估计值为
α=min{x
1,x
2,…,x
n},
于是α的最大似然估计量为
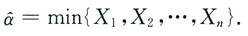
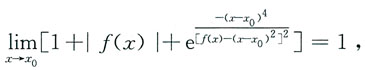 则______
则______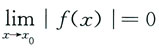 及
及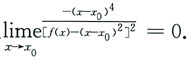 由于f(x)在x0处连续,所以由
由于f(x)在x0处连续,所以由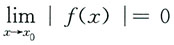 知f(x0)=0.又
知f(x0)=0.又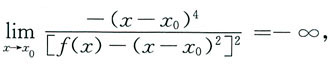 可知
可知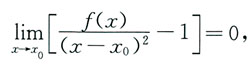 故
故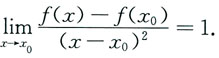 从而知存在δ>0,在x0的某空心邻域内f(x)-f(x0)>0,即x0是f(x)的极小值点,故选D.
从而知存在δ>0,在x0的某空心邻域内f(x)-f(x0)>0,即x0是f(x)的极小值点,故选D.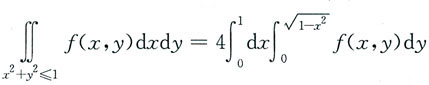 成立的充分条件是______
成立的充分条件是______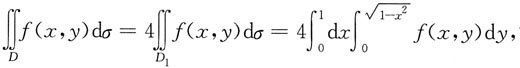 故选D.
故选D.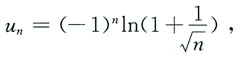 则级数______
则级数______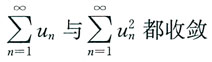
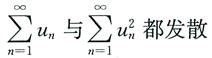
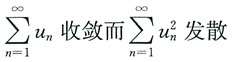

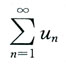 收敛,而
收敛,而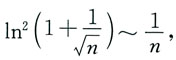 所以
所以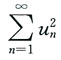 发散,故选C.
发散,故选C.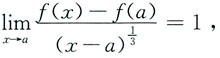 则函数f(x)在点a处必然______
则函数f(x)在点a处必然______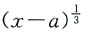 与x-a同号,因此
与x-a同号,因此 说明:存在δ>0,使得a<x<a+δ时,f(x)>f(a);同时,a-δ<x<a时,f(x)<f(a),故f(a)不是极值点,所以A,B均不正确.又因为
说明:存在δ>0,使得a<x<a+δ时,f(x)>f(a);同时,a-δ<x<a时,f(x)<f(a),故f(a)不是极值点,所以A,B均不正确.又因为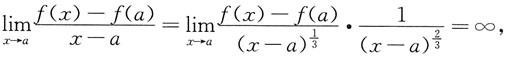 所以f(x)在a点不可导,C不正确,故选D.
所以f(x)在a点不可导,C不正确,故选D.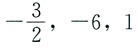
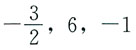
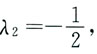 且有λ1λ2λ3=|A|=3,因此,λ3=3.又有Aξi=λiξi,i=1,2,3,在其两边同乘A*得
且有λ1λ2λ3=|A|=3,因此,λ3=3.又有Aξi=λiξi,i=1,2,3,在其两边同乘A*得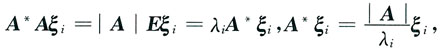
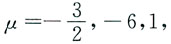 因此选A.
因此选A.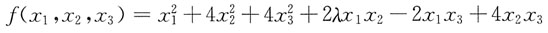 为正定二次型,则λ的取值范围是______
为正定二次型,则λ的取值范围是______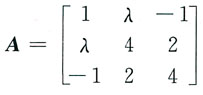 的各阶顺序主子式均大于0,即
的各阶顺序主子式均大于0,即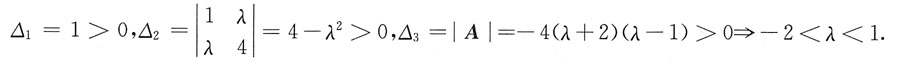 故选B.
故选B.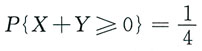
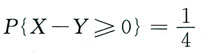
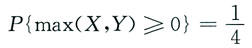

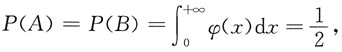 故
故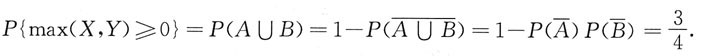 而
而 因此,选D.
因此,选D.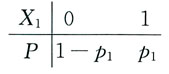
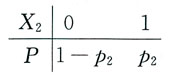
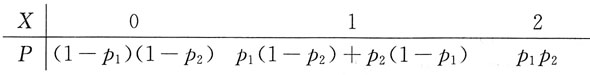
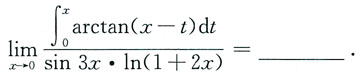
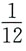
 于是
于是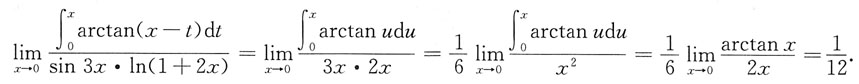
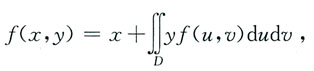 其中D是由
其中D是由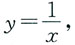 x=1,y=2所围区域,则f(x,y)=______.
x=1,y=2所围区域,则f(x,y)=______.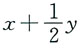
 则A为常数,此时f(x,y)=x+Ay.等式两边同时取二重积分得
则A为常数,此时f(x,y)=x+Ay.等式两边同时取二重积分得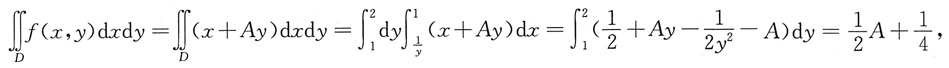 即
即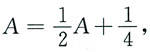 得
得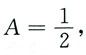 故
故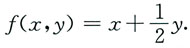
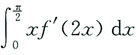 =______.
=______.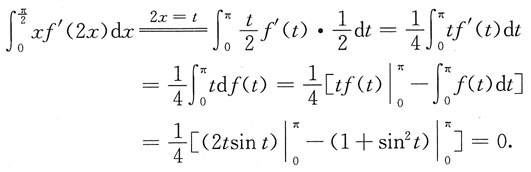
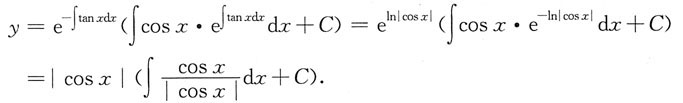
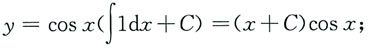
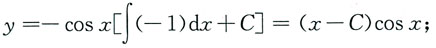
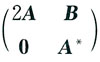 的特征值为______.
的特征值为______.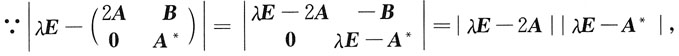 ∴只需分别求出2A,A*的特征值即可.设λ为A的特征值,则有Ax=λx,x≠0,于是2Ax=2λx,
∴只需分别求出2A,A*的特征值即可.设λ为A的特征值,则有Ax=λx,x≠0,于是2Ax=2λx,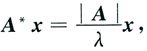 即2A,A*分别有特征值2λ,
即2A,A*分别有特征值2λ,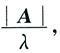 由题设λ1=1,λ2=2,λ3=3,且|A|=λ1λ2λ3=6,故所求特征值为2,4,6,6,3,2.
由题设λ1=1,λ2=2,λ3=3,且|A|=λ1λ2λ3=6,故所求特征值为2,4,6,6,3,2.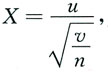 其中u~N(0,1),v~χ2(n),且u,v相互独立,于是
其中u~N(0,1),v~χ2(n),且u,v相互独立,于是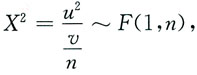 其中u2~χ2(1).
其中u2~χ2(1).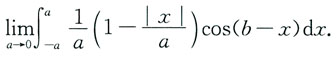
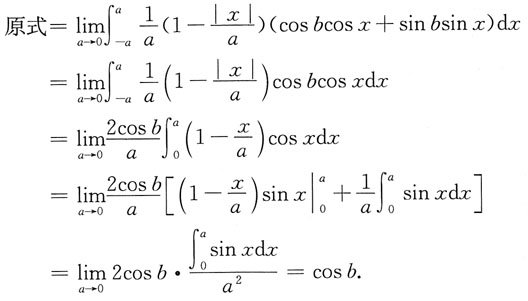
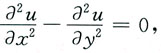 且u(x,2x)=x,ux(x,2x)=x2,求uxx(x,2x),uxy(x,2x),uyy(x,2x).
且u(x,2x)=x,ux(x,2x)=x2,求uxx(x,2x),uxy(x,2x),uyy(x,2x).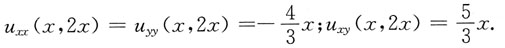
 L取正向.
L取正向.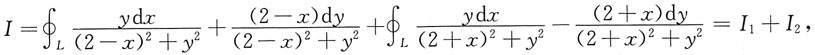
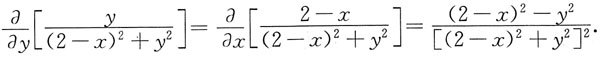
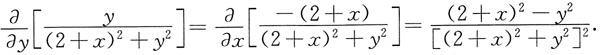
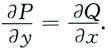
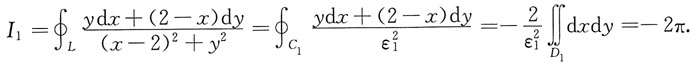
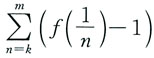 绝对收敛,其中k为足够大的正数.
绝对收敛,其中k为足够大的正数.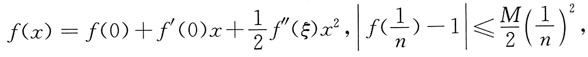 其中M=max{f"(x)}.
其中M=max{f"(x)}.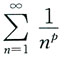 收敛,得原级数绝对收敛.
收敛,得原级数绝对收敛.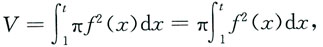
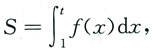
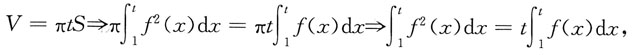
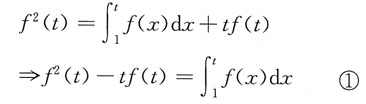
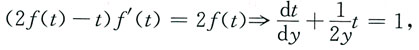

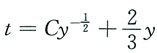 得
得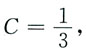

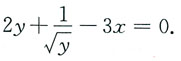
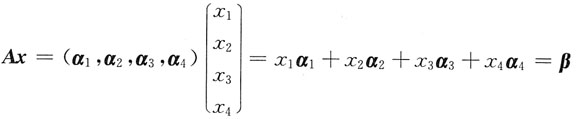



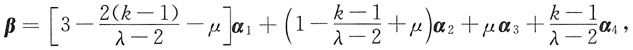
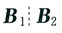 的形式,其中B1是r×r矩阵,B2=0,r(B1)=r,即存在可逆阵Q,使得BQ=B1B2.
的形式,其中B1是r×r矩阵,B2=0,r(B1)=r,即存在可逆阵Q,使得BQ=B1B2.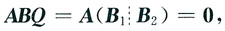 因而AB1=0,两边同乘
因而AB1=0,两边同乘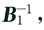 得A=0.
得A=0.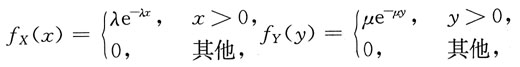
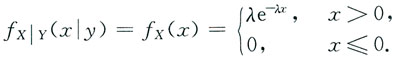
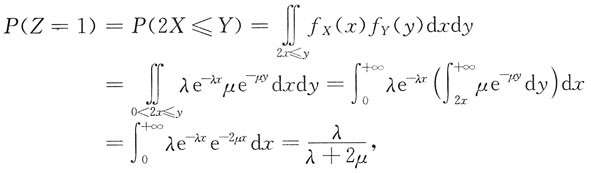
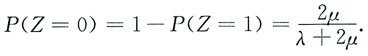
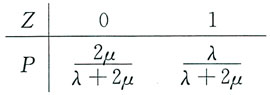

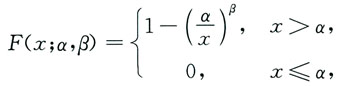
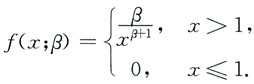
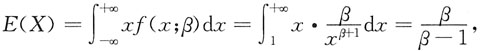
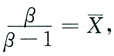 解得
解得
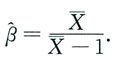

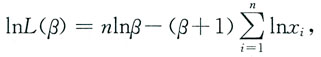
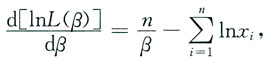
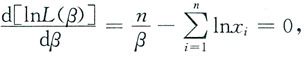 解得
解得